3. Неутронен пренос. Елементарна теория на дифузията, уравнение на дифузията, дифузионни характеристики на преносните среди. Пространствено и енергетично разпределение на неутроните в процеса на забавяне. Възрастово приближение.

Задачата за намиране на пространственото и енергетичното разпределение на неутроните в реактора, а оттам и на скоростите на всички неутронни реакции, се свежда до решаване на уравнението на неутронния пренос:

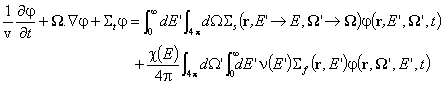
Тук v(E) е модулът на скоростта на неутроните, а търсеното решение е насочената плътност на неутронния поток , където N е неутронната плътност със следния физичен смисъл: е средният брой неутрони в момента t, които в обема dV около точката r имат посоки на движение в конуса dW около посоката W.

Уравнението на неутронния пренос е математичен израз на изискването за спазване на неутронния баланс във фазовия обем : “скорост на изменение не неутронната плътност” + “утечки” + “поглъщане и разсейване към други енергии или посоки” = “скорост на поява поради разсейване от други енергии или посоки” + “скорост на поява поради делене, предизвикано от неутрони с всякакви енергии и посоки”.

Тъй като решаването на това уравнение е изключително трудно, а скоростите на важните за практиката реакции (делене, поглъщане и т.н.) могат да се изразят и чрез скаларния поток , е целесъобразно да се състави уравнение относно F.

Записано за скаларния поток и тока, уравнението на неутронният баланс във фазовия обем е: . Това уравнение може да се реши само след въвеждане на връзка между тока J и потока F. Тази връзка, наречена закон на Фик, е: , където коефициентът на пропорционалност се нарича коефициент на дифузия. Законът на Фик е израз на твърдението, че резултантният неутронен пренос е по посока на максималното намаляване на потока и е пропорционален на това намаляване за единица дължина. Това твърдение е достатъчно обосновано само ако потокът е слабо анизотропен, т.е. неутроните се движат почти равновероятно във всички посоки, и ако поглъщането е пренебрежимо спрямо разсейването. Действително, при тези условия може да се очаква, че преносът ще бъде насочен главно от области с висока плътност на разсейването към такива с по-ниска.

Представа за физичния смисъл на дифузионния коефициент дава дължината на дифузия на топлинните неутрони . L² е числено равно на 1/6 от средния квадрат на разстоянието по права линия, изминавано от достигналия топлинна енергия неутрон при неговата дифузия до момента на поглъщането му.

Замествайки закона на Фик в балансното уравнение, се получава т.нар. дифузионно приближение на уравнението на неутронния пренос, или дифузионно уравнение: .

Зависимостта от времето често се елиминира чрез мащабиране на средния брой неутрони от делене n с условен множител, така че верижната реакция да бъде стационарна: . Множителят l има смисъл на ефективен коефициент на размножение k_eff. Той е числено равен на отношението на пълната скорост на поява не неутрони в реактора (от делене) към пълната скорост на загуба на неутрони (от поглъщане и утечка). Доколкото никой не може да влияе на броя неутрони от делене, стойността на l се използува само за указание как да се варират свойствата на реактора (напр. борна концентрация, положение на ОР СУЗ и т.н.), така че да се постигне l = 1, т.е. критично състояние.

Тъй като енергетичната зависимост на сеченията е извънредно сложна, а и в действителност неутроните при разсейване менят енергията си със скок, техният енергетичен диапазон (от 0 до напр. 15 MeV) се разделя на подинтервали , номерирани по посока на намаляване на енергията и наричани енергетични групи, така че да се получи система от уравнения за груповите потоци : . Коефициентите в тези уравнения (D_g, S_g и т.н.) се определят по специален начин, така че скоростите на реакциите да съвпадат с действителните (напр. ).

Пример за използуване на дифузионното уравнение е задачата за намиране на пространственото и енергетичното разпределение на неутроните в голям хомогенен (или условно хомогенизиран) критичен реактор без отражател. В този случай се разглеждат две групи, топлинна и надтоплинна, с енергетична граница между тях напр. 0.625 eV. Пространствено-енергетичното разпределение в надтоплинната група се описва от възрастовото уравнение , а в топлинната - от дифузионното уравнение . За съвместното решаване на тези две уравнения се въвеждат следните връзки между тях. Пренебрегвайки поглъщането в процеса на забавяне, източникът на топлинни неутрони се приема за равен на броя на неутроните, достигащи за единица време топлинна енергия, т.е. на плътността на забавяне до възрастта на топлинните неутрони . Пренебрегвайки деленето с бързи неутрони, плътността на забавяне на неутроните с енергията на източника се приема за равна на скоростта на генерация на неутрони от делене .

Описаният подход се нарича дифузионно-възрастово приближение. Това приближение е приложимо само за опростения случай на хомогенен реактор без отражател и може да послужи единствено за добиване на качествена представа за пространствено-енергетичното разпределение на неутроните в реалните реактори.