10. Кинетика на реактор с обратни връзки по реактивност

Действието на ефектите на реактивността върху кинетиката на реактора води до поведение, съществено различно от описаното в раздел 7. При известни (в резултат на неутронно-физични пресмятания и експерименти) коефициенти на реактивността - по температура на топлоносителя, температура на горивото и по мощност; както и при зададен закон на изменение на положението на ОР на СУЗ и на концентрацията на бор, уравненията на кинетиката могат да се модифицират по подходящ начин и да се опише (предвиди) поведението на реактора при преходни процеси.

За анализиране на временния ход на интегралната мощност на реактора и на реактивностния баланс е достатъчно точковото приближение на уравненията на кинетиката при известни (определени чрез неутронно-физични пресмятания) параметри на кинетиката.

Ако по време на преходния процес се изменя интегралната мощност на реактора при постоянна входна температура на топлоносителя, за отчитане на обратната връзка по реактивност е достатъчно да се знае мощностния коефициент на реактивността , където W е пълната топлинна мощност на реактора.

При известен закон на изменение на реактивността r(t) уравненията на кинетиката (7.9) могат да се решат спрямо топлинната мощност W(t), тъй като тя е пропорционална на пълния източник на неутрони в активната зона. От своя страна r(t) е функция на W(t):

10.1

DW(t)W(t)-W₀ е изменението на мощността спрямо началната стационарна стойност W₀. DH(t) и DC_B(t) са законите за изменение на височината на ОР на СУЗ и на концентрацията на разтворим бор, а и са диференциалните ефективности на съответните ОР на СУЗ и на борното регулиране.

Кинетиката на реактора с обратна връзка по мощност се описва от системата от уравнения (7.9) и (10.1). Решаването на тази система се прави числено, но процедурата е съвсем проста. Резултатът дава възможност да се предвиди мощността W(t) и балансът на реактивността по време на преходния процес.

Ако по време на преходния процес параметрите на активната зона се различават съществено от номиналните, за които е определен мощностния коефициент, отчитането на различните ефекти на реактивността трябва да става поотделно по температура на горивото T_U и температура на топлоносителя T_C. За намирането на тези температури са нужни съответни термохидравлични модели.

Опростен модел на температурната обратна връзка може да се направи, ако за описание на температурното поле в елементарната клетка се използува средната температура на горивото T_U и средната температура на топлоносителя Т_C. Уравненията на обратната връзка се съставят по следния начин. Балансът на реактивността е :

10.2

DT_C(t) º T_C(t)-T_C0 и DT_U(t) º T_U(t)-T_U0 са измененията на средните температури на топлоносителя и на горивото спрямо началните им стационарни стойности T_C0 и T_U0.

Диференциалното уравнение, описващо изменението на T_U, е уравнението на топлинния баланс на горивото:

"скорост на изменение на вътрешната енергия на горивото"

="топлинна мощност"

-"топлопредаване към топлоносителя

Или:

10.3

m_U е масата на ядреното гориво, c_U е специфичната му топлоемкост, k е коефициентът на топлопредаване от горивото към топлоносителя, S_U е площта на топлоотделящите елементи, W(t) е моментната мощност на реактора. Първият член отдясно е скоростта на нагряване на ТОЕ поради отделяната в горивото топлинна мощност. Вторият член отчита охлаждането на ТОЕ чрез топлопредаване към топлоносителя.

Диференциалното уравнение за T_C описва топлинния баланс на топлоносителя. Скоростта на охлаждане на топлоносителя в активната зона е c_CGDT_C, където c_C е специфичната топлоемкост на топлоносителя, G е масовият разход през активната зона, а DT_C е подгряването. Може да се приеме, че T_C @ T_вх. + 0.5DT_C. Тогава топлинният баланс на топлоносителя, изразен чрез средната му температура, е:

m_C е масата на топлоносителя, а T_вх. е входната му температура.

Или:

10.4

В стационарен режим и при липса на топлинни загуби температурата на топлоносителя на изхода на активната зона T_изх. @ 2T_C - T_вх. е равна на температурата на входа на парогенератора T_S. В нестационарен режим това равенство се нарушава поради факта, че за преместване на температурната вълна от реактора до парогенератора е нужно определено време t, наречено време на транспортно закъснение. То е от порядъка на няколко секунди и за ВВЕР-440 и 1000 експериментално определената му стойност е »5 s. Връзката между T_изх. и T_S.е:

10.5

Ако се приеме, че транспортното закъснение в обратната посока - по тракта "парогенератор-реактор" е малко, и се пренебрегне инерционността на топлообмена в парогенератора, системата от уравнения на топлинния баланс може да се затвори с топлинния баланс на парогенератора:

10.6

W_S е отдаваната в парогенератора мощност.

Системата от уравнения на кинетиката се затваря чрез добавяне към горните уравнения на системата (7.9) от уравнения на кинетиката на "студен" реактор.

Решението на тази система зависи от началните условия: . Решаването й става числено. За тази цел е нужно да се знаят коефициентите в уравнения (10.3)-(10.6) Това са: m_C, c_C, m_U, c_U, k, S_U,t, G, W_S. Някои от тях, като G и W_S пряко се контролират при работата на реактора и по принцип са известни. Параметрите на топлоносителя m_C и c_C могат да се намерят от конструктивните характеристики на реактора и топлофизичните свойства на водата. Важно е да се помни, че m_C и c_C зависят от температурата T_C и налягането на топлоносителя в активната зона. Транспортното закъснение t се пресмята по-трудно, но може да бъде оценено експериментално. Ефектът от t се проявява само при бързопротичащи преходни процеси. Масата и топлоемкостта на горивото и конструкционните материали, както и произведението kS_U зависят от много фактори и тяхното точно пресмятане е трудно.

Задаването на началните условия и на коефициентите на системата може да се улесни при отчитане на особеностите на работа на реактора в стационарен режим. Ако в момента t=0 параметрите на активната зона са постоянни, то:

- разходът G, входната температура и изходната температура на топлоносителя и топлинната мощност W са пряко измерими и известни.

- изходната температура на топлоносителя от активната зона е равна на температурата на входа на парогенератора :

-отвежданата от парогенератора мощност W_S е равна на генерираната в активната зона W(0): W_S = W(0). Разглежданият модел на кинетиката по принцип е полезен само при бързи преходни процеси, когато W_S е практически постоянна величина, така че горното равенство определя един от коефициентите на системата. При бавни преходни процеси, когато W_S(t) = W(t), средната температура на топлоносителя T_C остава практически постоянна и за моделиране на динамиката на реактора е по-уместно да се използува дефинираният при тези условия мощностен коефициент на реактивността, който отчита главно ефекта от температурата на горивото T_U.

Остават неопределени произведенията m_Uc_U и kS_U, както и началната температура на горивото T_U(0). Те могат да бъдат намерени по следния начин.

При описаните условия четирите уравнения (10.3)-(10.6) се свеждат само до две - (10.3) и (10.4) с нулеви леви страни. Така те могат да се разглеждат като алгебрични уравнения за определяне на неизвестните m_Uc_U, kS_U и Т_U(0). Тъй като от две уравнения не могат да се определят едновременно и трите неизвестни величини, е нужно да се разгледа още едно допълнително стационарно състояние. Ако (10.3) и (10.4) се приложат за две състояния, характеризиращи се с мощности на реактора W₁ и W₂, и ако W₁ и W₂, са достатъчно близки, така че m_Uc_U, и kS_U да останат приблизително постоянни, то получената система от 4 уравнения може да се реши за четирите неизвестни m_Uc_U, kS_U Т_U1(0) и Т_U2(0). Т_U1(0) и Т_U2(0) са съответните температури на горивото. Едно от двете състояния се избира да бъде началното. Така началните условия и коефициентите на уравненията на кинетиката на реактора с обратни връзки по температури на горивото и на топлоносителя стават напълно определени.

Този модел на кинетиката може да се използува за анализ на поведението на реактора при бързи преходни процеси и при параметри на активната зона, отличаващи се от стандартните.

С него може да се анализира например така наречената "повторна критичност" при охлаждане на активната зона. В края на кампанията, когато концентрацията на бор е минимална или нулева, коефициентът на реактивност по температура на топлоносителя става голям по абсолютна стойност и е отрицателен. При спиране на реактора (освободен мощностен ефект) и разхлаждане на активната зона размножаващите й свойства се подобряват, тъй като липсва или е малък ефектът от повишаване на ядрената концентрация на бор при увеличаване на плътността на топлоносителя. Ако сумарната подкритичност, въведена от спуснатите ОР на СУЗ не е достатъчна за компенсиране на освобождавания температурен ефект, при достигане на определена температура може да настъпи критичност и евентуална надкритичност. Реакторът ще се стабилизира за сметка на доплеровия ефект, но биха настъпили осцилации. Изход от ситуацията е при разхлаждане на активната зона да се поддържа безопасно висока концентрация на бор в топлоносителя.

Пример:

При скокообразна промяна на реактивността на реактор, работещ в стационарен режим (Фиг.10.1), реакторът се стабилизира на по-високо ниво на мощност при положителен скок на реактивността поради отрицателен мощностен коефициент на реактивност - "внесената" положителна реактивност се компенсира от отрицателна реактивност от отрицателния мощностен коефциент на реактивност. При внесена отрицателна реактивност реакторът се стабилизира на по-ниско ниво на мощност поради освободена положителна реактивност от мощностния коефициент на реактивност. При всички реални процеси в обратните връзки има принос и промяната в средната температура на топлоносителя.

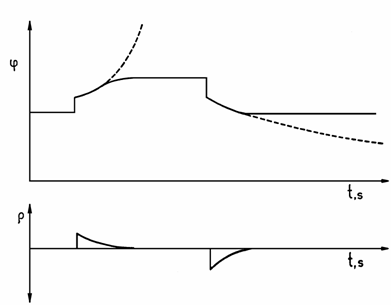
Фиг.10.1. Стабилизиране на мощността на реактора при положителен и отрицателен скок на реактивността поради отрицателна обратна връзка (виж раздел 16).

ВЪПРОСИ И ЗАДАЧИ

1)При работа на 50% N_ном и повдигане на ОР със 7.5 cm, реакторът се стабилизира на по-висока мощност. Какво е новото ниво на мощност?

Упътване:

Въведената положителна реактивност от ОР се компенсира от отрицателния мощностен ефект и сумарната реактивност е отново 0:

2.При сработване на системата за УРБ при N_ном=100%, група No.1 е въведена в АЗ за време 1.5-4 s. Пресметнете каква реактивност е необходимо да се въведе допълнително от групи 10, 9, 8, ако целта е да се намали мощността до 50% N_ном.

Упътване:

3. Нека в критичен реактор височината на ОР на СУЗ е H₀ и в момента t₀ тя се изменя с DH. Напишете уравненията на кинетиката с обратни връзки по реактивност при предположение, че входната температура на топлоносителя се поддържа постоянна. Опишете начин за решаване на тези уравнения.

Упътване:

Зададената реактивност при известна диференциална ефективност на ОР на СУЗ и малко изменение DH e:

При постоянна входна температура обратната връзка може да се отчете единствено с мощностния коефициент на реактивността и действителната реактивност е:

W(t) е мощността на реактора по време на преходния процес, а W₀ е началната й стойност. W(t) обаче може да се намери от уравненията на кинетиката само ако е известна действителната реактивност във всеки момент. Следователно горното уравнение може да се използува само в система с уравненията на кинетиката:

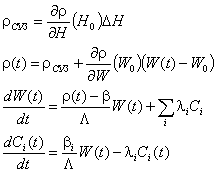
при начални условия:

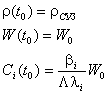
Подходът за решаване на тази система може да бъде следният:

Ако за много малкия интервал dt се допусне, че реактивността остава практически постоянна и равна на (t), а мощността и концентрациите на ядра-предшественици - постоянни и равни на W(t) и C_i(t), то:

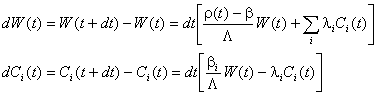
Така можем да намерим r(t+dt) W(t+dt) и C_i(t+dt):

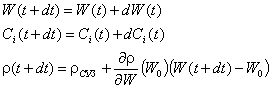
Започваме процедурата от t=t₀ и намираме решението за t=t₀+dt, след това я повтаряме и намираме решението за t=t₀+2dt, и така нататък.

4) Напишете уравнението за топлинния баланс на горивото и го използувайте, за да получите диференциално уравнение за температурата на горивото.

5) Оценете повишението/понижението на мощността на реактора с обратни връзки по мощност при преместване на регулиращата група с 5 cm, 10 cm нагоре и надолу от положението К_eff = 1. Приемете диференциална ефективност на ОР 210^-3 %/см. Използвайте данни за dr/dN от таблицата от Приложението на раздел 9.

Упътване:

При въвеждане на положителна/отрицателна реактивност чрез преместване на ОР на СУЗ мощността на реактора ще расте/намалява докато реактивността е различна от нула. Ако обратните връзки не са достатъчни да компенсират тази реактивност, в крайна сметка мощността на реактора ще достигне безкрайност/нула. Ако в някакъв късен момент обратните връзки компенсират реактивността и тя стане нула, реакторът ще се стабилизира при ниво на мощността, което зависи от този момент и от хода на реактивността междувременно. Задачата може да се реши числено по подхода, описан в упътването на задача (1). В специалния случай, когато отрицателната обратна връзка по мощност "мигновено" компенсира въведената реактивност, задачата може да се реши просто в приближението на "мигновения скок" на уравненията на кинетиката с една група закъсняващи неутрони. Уравненията на кинетиката са:

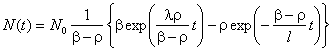
При преместване на ОР с 5 cm нагоре, въведената реактивност е 10^-2%.

При =0.0070, l=6.10^-5 s и l=0.08 s^-1,

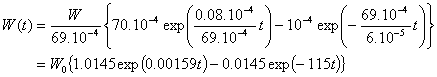
Втората експонента е с нищожна амплитуда и изчезва след 0.04 s, за което време първият член, който нараства с период 629 s изобщо не се променя. Следователно мощността нараства мигновено до 1.0145W₀, a след това би започнала бавно да се покачва, ако реактивността остане 10^-2 %. При номинална мощност 3000 MW мигновеният скок е 43.5 MW. Мощностният коефициент е -0.249.10^-3 %/MW и следователно намаляването на реактивността е 43.5.(-0.249).10^-3 % = -1.08.10^-2 %. Получава се, че действителната реактивност е (1-1.08).10^-2 %, което е практически нула. Резултатът е че след мигновения скок реакторът отново е критичен и запазва достигнатата мощност 3043.5 MW.

При преместване на ОР с 10 cm нагоре всичко е практически същото, освен че мигновеният скок е два пъти по-голям. Въведената реактивност е също два пъти по-голяма, както и мощностния ефект. Реакторът отново се оказва критичен след мигновения скок при мощност 3087 MW.

В общия случай, когато r₀ << b, мигновеният скок е

Реакторът ще се окаже критичен след мигновения скок, ако

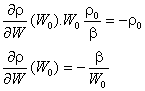
В хода на кампанията мощностният коефициент нараства, вместо да намалява с , така че след мигновения скок реакторът се оказва подкритичен и ще се стабилизира на по-ниска от оценената, но по-висока от началната мощност. От втората таблица пък се вижда, че при ниска мощност мощностният коефициент не е достатъчно голям и реакторът ще се окаже надкритичен след мигновения скок, поради което ще се стабилизира на по-висока мощност от оценената.