1. Делене на ядрата под действието на неутроните. Механизъм на деленето. Продукти на деленето. Сечения на взаимодействие на неутроните с ядрата.

Механизъм на ядреното делене

Средната енергия на свързване на един нуклон в атомното ядро достига максималната стойност 8.7 MeV при ядра с масово число около 50. Следователно, чрез сливане на по-леки ядра (ядрен синтез), или чрез предизвикване на разделянето на едно тежко ядро на две или повече ядра с междинни маси (ядрено делене), е възможно да бъдат образувани по-здраво свързани ядра и да бъде освободена енергия.

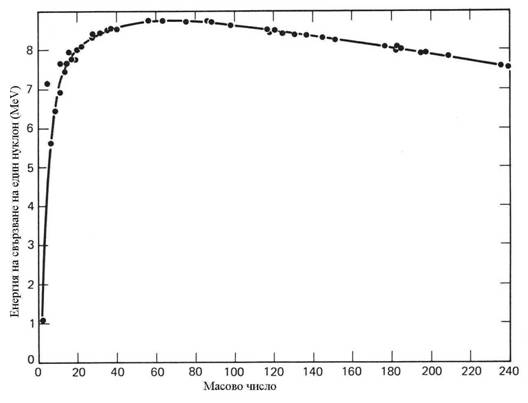
Наблюдаваната стабилност на тежките ядра по отношение на спонтанно делене се дължи на близкодействуващите ядрени сили между нуклоните в ядрото, водещи до възникването на потенциална енергетична бариера, която трябва да бъде преодоляна, за да настъпи делене. Височината на тази бариера при повечето тежки ядра, представляващи интерес от гледна точка на верижната реакция на делене, е типично 6-9 MeV.

Следователно, за да бъде предизвикано делене, на тежкото ядро трябва да се придаде достатъчна енергия за преодоляване на потенциалната бариера. Това може да бъде постигнато по различни начини. Един от тях е чрез стълкновение на високоенергетична частица с ядрото (с кинетична енергия, надхвърляща енергетичната бариера за делене). Пример за такава реакция е фотоделенето, предизвиквано от стълкновение на високоенергетичен гама квант с тежкото ядро. Алтернативна възможност е да се създадат условия за залавяне на неутрон от тежкото ядро. Тогава за преодоляване на енергетичната бариера и предизвикване на делене може да се окаже достатъчна и само енергията на свързване на заловения неутрон.

Последният процес може действително да настъпи при някои тежки ядра, като напр. ²³³U, ²³⁵U, ²³⁹Pu и ²⁴¹Pu. Такива нуклиди, чието делене може да настъпи при залавянето на неутрони с практически нулева кинетична енергия, се наричат делящи се. Делящите се нуклиди са главни компоненти на горивото в ядрените реактори.

При повечето тежки нуклиди допълнителната енергия на свързване на заловения неутрон не е достатъчна за преодоляване на енергетичната бариера за делене. При някои от тях, обаче, тази бариера може да бъде преодоляна, ако заловеният неутрон притежава кинетична енергия от порядъка на 1 MeV. Нуклидите, които могат да се делят при залавяне на такива “бързи” неутрони, се наричат делими. Примери за такива нуклиди са ²³²Th, ²³⁸U и ²⁴⁰Pu (както, естествено и делящите се нуклиди като ²³⁵U или ²³⁹Pu).

При някои тежки ядра съществува и известна малка вероятност за спонтанно делене чрез преодоляване на потенциалната бариера в следствие на познатия от квантовата механика тунелен ефект. При повечето нуклиди, намиращи приложение като ядрено гориво, вероятността за такова събитие е действително твърде малка. Например, периодът на полуразпадане на ²³⁸U чрез спонтанно делене е 6.5x10¹⁵ години. Даже и тази много ниска скорост на спонтанно делене може обаче да бъде от значение за ядрените реактори, тъй като незначителният брой възникващи при това неутрони могат да бъдат много бързо размножени в процеса на верижната реакция.

Продукти на деленето

При една типична реакция на ядрено делене, като напр.

възникват разнообразни продукти, сред които са дъщерните ядра (фрагменти от деленето), няколко неутрона и множество гама кванти, бета частици и неутрино. Отделя се и значителна енергия - приблизително 200 MeV.

Ядрото се дели почти винаги на два фрагмента, чието разпределение по маси и атомни номера има случаен характер. Поради някои фактори, определящи ядрената стабилност и обусловени от броя и вида на частиците в ядрото, вероятността двата фрагмента да бъдат еднакви е малка. Кривата на разпределението на фрагментите по маса има два ясно изразени максимума - около A=95 и A=135. С увеличаване на енергията на неутроните, предизвикващи деленето, това разпределение става все по-равномерно. Фрагментите от деленето са силно йонизирани и с голяма кинетична енергия. Те се забавят и неутрализират чрез удари с атомите на веществото в непосредствена близост до мястото на своето възникване. Такъв е всъщност главният механизъм за освобождаване на енергията от деленето във вид на топлина в материала на ядреното гориво. Тези фрагменти са обикновено и твърде нестабилни по отношение на своя нуклонен състав. Като правило те достигат стабилност посредством серия от b-разпадания, съпроводени с изпускане на g-кванти, при което атомният им номер нараства (част от неутроните се превръщат в протони). Енергията от тези разпадания може да достигне 4-5% от пълната енергия от деленето, а нейното освобождаване става със значително закъснение, обусловено от периодите на полуразпадане на ядрата във веригата. Енергията на b-частиците се предава на веществото във вид на топлина практически на място, а енергията на g-квантите - в радиус от порядъка на сантиметри.

Броят на освобождаваните неутрони може да бъде различен при всеки индивидуален акт на делене, но техният среден брой n е напълно определен и зависи от делящия се нуклид и енергията на предизвикалия деленето неутрон E. Тук е уместно да се отбележи, че именно освобождаваните при деленето неутрони правят възможна самоподдържащата се верижна реакция на делене. Повечето от тях възникват практически незабавно след деленето (в рамките на 10^-14 s) и се наричат мигновени. Известна част, обаче, (под 1%) се появяват със значително закъснение като продукт на радиоактивното разпадане на ядрата-фрагменти. Относителният дял на тези закъсняващи неутрони също зависи от вида на делящия се нуклид и от енергията на неутрона, предизвикал деленето. Тяхното съществуване е най-важната и абсолютно необходима предпоставка за управляемостта на верижната реакция на делене. Пълният брой неутрони от делене n(E) (мигновени плюс закъсняващи) нараства с енергията на предизвикалия деленето неутрон (E £ 15 MeV) и за някои от най-важните делящи се нуклиди, при измерване на енергията в MeV, е:

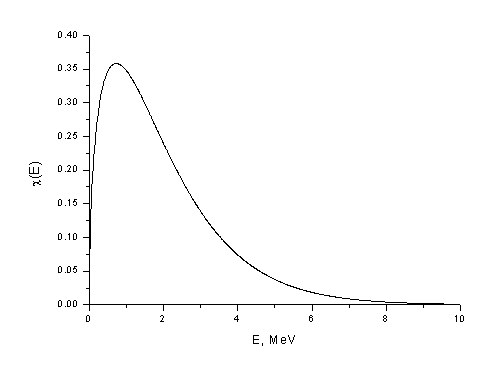
Вероятностното разпределение на неутроните от делене по енергия зависи от делящия се нуклид и в по-малка степен от енергията на предизвикалия деленето неутрон, и е различно за мигновените и закъсняващите неутрони. За характеризиране на това разпределение е удобно да се въведе енергетичен спектър на неутроните от делене, или спектър на делене, c(E), определен като:

c(E)dE º среден относителен брой неутрони от делене, възникващи в интервала от Е до E+dE.

С достатъчна точност спектрите на делене мога да бъдат представени чрез прости емпирични изрази. Така например, спектърът на мигновените неутрони от делене на ²³⁵U при измерване на енергията в MeV е:

Поради важността на закъсняващите неутрони за управлението на верижната реакция е уместно да се разгледа накратко механизмът на тяхното възникване и да се въведат някои основни понятия, използувани за тяхното описване.

Закъсняващите неутрони се изпускат незабавно след първото b-разпадане на някои от фрагментите на деленето, наречени ядра-предшественици. Продуктът на разпадането на ядрото-предшественик се образува във възбудено състояние и е нестабилен по отношение на своето неутронно съдържание. За достигане на стабилност той подлежи на едно или повече допълнителни b-разпадания, при които съответният брой неутрони в ядрото се превръщат в протони. Когато енергията на възбуждане на такова ядро надхвърля енергията на свързване на един неутрон в него, същият резултат може да се постигне и чрез изпускане на неутрон. Процесът протича съгласно познатия експоненциален закон за радиоактивно разпадане. Пример за верига от превръщания, водеща до изпускане на закъсняващ неутрон, е:

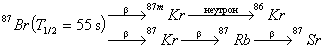
В случая закъснението на неутрона след момента на делене се обуславя от b-разпадането на ⁸⁷Br.

При верижната реакция на делене възникват десетки различни ядра-предшественици, но за целите на реакторния анализ е общоприето и достатъчно точно те да се обединяват по периоди на полуразпадане в 6 групи със следните характеристики:

l_i, i=1,...,6: константи на разпадане на групите ядра-предшественици;

b_i, i=1,...,6: относителни дялове (спрямо пълния брой неутрони от делене) на закъсняващите неутрони, изпускани от ядрата-предшественици във всяка група;

: относителен дял на закъсняващите неутрони спрямо пълния брой неутрони от делене;

c_i(E): спектри на закъсняващите неутрони, изпускани от групите ядра-предшественици.

Тъй като относителният добив на ядра-предшественици от индивидуалните делящи се (или делими) нуклиди е различен, характеристиките на тези 6 групи са специфични за всеки нуклид. За главните нуклиди в горивото на реакторите ВВЕР те са:

нукл.	^235U		^238U		^239Pu		^241Pu
гр.	bi	li, s^-1	bi	li, s^-1	bi	li, s^-1	bi	li, s^-1
1	2.50E-04	0.0133	2.02E-04	0.0136	6.60E-05	0.0133	8.82E-05	0.0137
2	1.26E-03	0.0325	1.64E-03	0.0313	5.65E-04	0.0302	1.27E-03	0.0299
3	1.08E-03	0.122	1.91E-03	0.123	3.94E-04	0.113	7.79E-04	0.114
4	2.26E-03	0.314	5.62E-03	0.324	7.09E-04	0.295	1.82E-03	0.308
5	1.15E-03	0.9.60	3.70E-03	0.906	3.20E-04	0.854	1.00E-03	0.859
6	5.88E-04	2.94	1.50E-03	3.05	1.04E-04	2.63	3.32E-04	3.067
общо	6.59E-03		1.46E-02		2.16E-03		5.29E-03

Важно е да се отбележи, че средните енергии на закъсняващите неутрони са няколкостотин keV и са значително по-ниски от средната енергия на мигновените неутрони, която е около 2 MeV. По тази причина те имат различна относителна ценност за поддържане на верижната реакция на делене в сравнение с мигновените. Така например, за реактори от типа ВВЕР ценността на закъсняващите неутрони, които поради недостатъчната си енергия не могат да предизвикат делене на ²³⁸U, е по-ниска от тази на мигновените.

Енергия от деленето

Двата фрагмента, на които се разделя ядрото, са положително заредени и се раздалечават под действието на кулоновата сила на отблъскване, отдавайки във вид на топлина (отново чрез кулоново взаимодействие) своята кинетична енергия (»168 MeV) на ядрата на околното вещество в радиус »10^-3 cm от мястото на деленето. Така около 82% от пълната освободена при деленето енергия се превръща мигновено в топлина на мястото, където е протекло деленето.

Пълната кинетична енергия на неутроните от деленето е »5 МeV. Тя се превръща в топлина посредством многократни сблъсъци на неутроните с ядрата на веществото на активната зона в област с радиус няколко сантиметра. Ако не напуснат реактора и не бъдат погълнати, неутроните се забавят докато тяхната средна енергия стане близка до кинетичната енергия на атомите на веществото (»0.025 eV), което съответствува на скорост »2200 m/s. В крайна сметка (след 10^-3 до 10^-7 s, в зависимост от състава на средата) неутроните биват погълнати. Важно е да се отбележи, че докато енергията на фрагментите от делене се превръща в топлина в горивото, то енергията на неутроните се отдава във вид на топлина предимно в топлоносителя. Причина за това е, че при удар с леко ядро (водород, кислород) неутронът отдава много повече енергия, отколкото при удар с тежко ядро (уран). При удар с ядро на водород неутронът губи средно 37% от енергията си, а при удар с ядро на ²³⁸U - само 0.9%. Времето за забавяне на неутрона е около 10^-5 s.

Мигновено изпусканите при деленето g-кванти и изпусканите по-късно от продуктите от деленето добавят към енергоотделянето по около 7 MeV. Енергията, освобождавана във вид на g-кванти при неутронно залавяне от материалите в активната зона зависи от залавящото вещество, но е обикновено в диапазона 3-12 MeV. Въпреки че тези g-кванти не са пряк резултат от деленето, те се включват в общия баланс на енергията, освобождавана при делене, тъй като винаги съпровождат този процес и допринасят за общото енергоотделяне в реактора. g-квантите отдават своята енергия на веществото в активната зона във вид на топлина в радиус от порядъка на сантиметри. Утечката както на неутрони, така и на g-кванти при големите енергетични реактори е от порядъка на проценти и по отношение на баланса на енергоотделянето може да се пренебрегне.

b-частиците, освобождавани при радиоактивно разпадане на фрагментите на делене, имат средна обща енергия около 8 MeV на един акт на делене и отдават своята енергия на веществото практически на място. Тъй като радиоактивното разпадане може да бъде бавен процес, енергията на b-частиците и g-квантите от фрагментите на деленето и на g-квантите от неутронно залавяне се отдава във вид на топлина сравнително бавно. Средно фрагментите от деленето от един акт на делене се разпадат с времето приблизително като : . Ако реакторът е работил достатъчно дълго време на постоянна мощност, съответствуваща на F деления/s, а след това в момента t₀<t е бил спрян, трябва да се интегрира средната скорост на разпадане P_d(t) от всички предходни деления: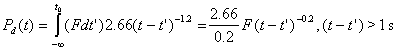

Около 12 MeV от енергията от деленето се отнася от неутриното, което практически не взаимодействува с веществото. Тази загуба почти се компенсира от енергията на g-квантите от радиационно залавяне на неутрони от веществото в активната зона, така че 200 MeV е добро приближение за освободената в реактора енергия в резултат на деленето.

Енергетичният баланс от делене е обобщен в долната таблица:

произход	МеV	разпространение
кинетична енергия на фрагментите на делене	165	в горивото
кинетична енергия на мигновените неутрони	»5	в топлоносителя
енергия на g-квантите, излъчвани в момента на делене	»7	предимно в горивото
енергия на b-разпадането на продуктите на делене	»7	в горивото
енергия на g-квантите от разпадане на продукти на деленето	»7	предимно в горивото
енергия на g-квантите от радиационно залавяне на неутрони	»7	предимно в горивото
енергия на антинеутринното лъчение	»10	губи се

Сечения за взаимодействие на неутроните с ядрата

Процесите на взаимодействие на неутроните с веществото, както и изобщо квантовите събития, се описват единствено със своите вероятности. За количествено представяне на тези вероятности се използува условната величина ядрено сечение.

Микроскопични сечения

Нека сноп неутрони, всичките с еднаква скорост и посока на движение, пада нормално и равномерно върху плоска мишена, съставена от еднородно вещество (напр. чист ²³⁵U). Ако мишената е достатъчно тънка, така че ядрата в нея да не се засенчва взаимно от падащия неутронен сноп, би следвало да се очаква, че скоростта (честотата) на реакцията между неутроните и ядрата ще бъде пропорционална на интензитета на снопа I (бр. неутрони/(cm².s)) и на броя ядра на единица площ от мишената N_s (бр. ядра/cm²). Означавайки въпросния коефициент на пропорционалност със s, скоростта на реакцията ще бъде:

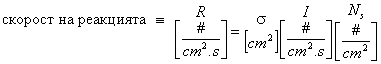
От израза следва, че коефициентът на пропорционалност s ще има размерност на площ. Ако си представим неутроните и ядрата като класически частици, s ще съответствува на площта на проекцията на мишената-ядро в равнина, перпендикулярна на посоката на движение на неутрона. В съгласие с тази представа величината s, характеризираща вероятността за взаимодействие на едно ядро с неутрон, е прието да се нарича микроскопично сечение. Тъй като ядрените радиуси са от порядъка на 10^-12 cm, геометричните сечения на ядрата ще бъдат съизмерими с 10^-24 cm². Такава е и общоприетата количествена мярка за микроскопичните сечения, наричана barn (барн): 1 barn (1 b) = 10^-24 cm².

Приведената геометрична аналогия обаче може да бъде подвеждаща, тъй като s може да бъде много по-голямо (или по-малко) от геометричното сечение на ядрото. Една от причините за това са резонансните ефекти, които са следствие от квантовомеханичната природа на ядрото и на неутрона. Така например, сечението за поглъщане на нискоенергетични неутрони от е около милион пъти по-голямо от геометричното сечение на това ядро. Друга, отново квантовомеханична, причина е зависимостта на “ефективния размер” на неутрона от неговия импулс, поради което при ниски енергии микроскопичните сечения се менят с енергията на неутрона E приблизително пропорционално на . Микроскопичните сечения за взаимодействие с нискоенергетични неутрони се менят и в зависимост от температурата на средата, тъй като в действителност се определят от енергията на неутрона относно центъра на масите на системата неутрон-ядро.

Микроскопичните сечения се използуват за описване на вероятностите за различни типове реакции, напр. делене (n,f), радиационно залавяне (n,g), разсейване (n,n) и т.н. Съответните сечения се означават с s_f (делене), s_g (радиационно залавяне), s_s (разсейване). Процесите на разсейване от своя страна могат да се подразделят на еластично (n,n), при което ядрото-мишена остава в основно състояние (s_e) и нееластично (n,n’), при което ядрото-мишена остава във възбудено състояние (s_in). Тъй като сеченията са мярка за вероятност, е очевидно, че s_s = s_e + s_in. По подобен начин може да се дефинира сечение за поглъщане, s_a, отчитащо всички събития, при които неутронът се поглъща от ядрото. Съществуват редица реакции на поглъщане, включващи деленето, радиационното залавяне, (n,a) реакцията и т.н. Може да се въведе и понятието за пълно сечение, s_t, характеризиращо общата вероятност за взаимодействие. Очевидно, s_t = s_s + s_a = s_e + s_in + s_f + s_g + s_n,a + ...

Стандартни са и следните функции на ядрените сечения със съответните им обозначения:

Пълен брой неутрони от делене, отнесен към един акт на поглъщане на неутрон с енергия E от делящ се нуклид j:

Отношение на сечението за поглъщане, не водещо до делене, към сечението за делене на нуклида j с неутрони с енергия E: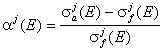

Стойностите s_a, s_f, a и h за делящите се нуклиди при енергия на неутроните 0.025 eV (съответствуваща на топлинно равновесие със средата при 20C) са:

	sa	sf	a	h
^233U	579	531	0.0899	2.287
^235U	681	582	0.169	2.068
Природен уран	7.59	4.19	0.811	1.335
^239Pu	1011	743	0.362	2.145

Макроскопични сечения

Ако предходният пример се модифицира за случая на дебела мишена, ще бъде нужно да се отчита и засенчването на ядрата от падащия сноп, тъй като взаимодействията извеждат неутрони от него. За отчитане на този ефект трябва да се състави уравнение за интензитета на снопа от невзаимодействували неутрони I(x) на дълбочина x в мишената. Да разгледаме тънък слой от мишената между x и x+dx. Тъй като неговата дебелина dx е безкрайно малка, за пресмятане на скоростта на взаимодействие в 1 cm² от слоя можем да използуваме резултата от анализа на разгледания вече пример. Отчитайки, че броят на ядрата в 1 cm² от слоя е dN_s = N_vdx, където N_v е броят ядра в 1 cm³ от мишената, пълната скорост на реакцията на единична площ от слоя ще бъде dR = s_tI(x)dN_s = s_tI(x)N_vdx. Тази скорост ще бъде точно равна на намаляването на интензитета на снопа между x и x+dx: -dI(x) = -[I(x+dx) - I(x)] = s_tI(x)N_vdx. След разделяне на dx се получава търсеното диференциално уравнение за интензитета на снопа I(x): dI(x)/dx = -N_vs_t I(x). Неговото решение е I(x) = I₀exp(-N_vs_t x), където I₀ е интензитетът на падащия сноп при x = 0.

Тъй като измерваното в cm^-1 произведение на обемната плътност на ядрата N_v по микроскопичното сечение s се среща много често в реакторния анализ, за него е въведено понятието макроскопично сечение: . Терминът “макроскопично” отразява обстоятелството, че S характеризира вероятността за неутронно взаимодействие в макроскопичен материален обем (за разлика от микроскопичното сечение s, характеризиращо вероятността за взаимодействие с единично ядро).

От диференциалното уравнение за интензитета на снопа I(x) следва интерпретацията на S като вероятност за взаимодействието на един неутрон при изминаване на път с единична дължина през съответната материална среда. Съгласно тази интерпретация, е вероятността един неутрон да измине разстояние x без взаимодействие, а е вероятността един неутрон да взаимодействува в слоя между x и x+dx. Следователно, средното разстояние, изминавано от неутрона преди взаимодействие с ядро в мишената, е 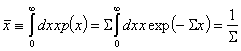. Прието е това разстояние да се наричан среден свободен пробег и да се означава с l.

Аналогично на случая с микроскопичните сечения, понятието за макроскопично сечение се обобщава чрез дефиниране на сечения за всяка конкретна реакция: S_a = N_vs_a, където индексът a обозначава типа на реакцията.

Ако материалната среда е хомогенна смес от повече от един нуклида, напр. X, Y, Z, а N_X, N_Y, N_Z са техните обемни ядрени концентрации [бр. ядра/cm³], то макроскопичното сечение на тази среда ще бъде: S = N_Xs^X + N_Ys^Y + N_Zs^Z.

Отчитайки зависимостта на микроскопичните сечения от енергията на неутрона и възможността материалната среда да бъде нееднородна и нейният състав да се мени с времето, в най-общия случай макроскопичното сечение ще се описва от израза: S(r,E,t) = N(r,t)s(E).

Характеристики на неутронните сечения

Сеченията за поглъщане на всички нуклиди имат енергетична зависимост, близка до при ниски енергии (<2 eV). Следователно, ако е сечението за поглъщане от нуклида j на неутрон с енергия 0.025 eV (т.е. при топлинно равновесие със средата при температура 300 K), съответното сечение за други енергии в нискоенергетичния диапазон ще бъде . Такова поведение на сечението се нарича "1/v", тъй като скоростта на неутрона v µ . Тази енергетична зависимост на сечението се обяснява с вълновата природа на неутрона - дължината на вълната на де Бройл за даден материален обект е l µ 1/p, където p е неговият импулс mv. Ефективният "размер" на неутрона е от порядъка на тази дължина на вълната и явно вероятността неутронът да попадне в обхвата на действие на ядрените сили, което е предпоставка за взаимодействие с дадено ядро, ще бъде пропорционална на този размер. При повечето леки елементи поведението 1/v се запазва до високи енергии.

При средните и тежките елементи обаче, започвайки от надтоплинната енергетична област, в зависимостта на от енергията E се наблюдават множество високи и тесни пикове. Те се обуславят от наличието на метастабилни енергетични нива на възбуденото съставно ядро. Ако кинетичната енергия на налитащия неутрон е такава, че при добавянето й към потенциалната енергия, придобита от ядрото при поглъщането на този неутрон, енергията на възбуждане на полученото ядро се изравни с енергията на някое негово метастабилно състояние, то образуването на това съставно ядро настъпва с много висока вероятност. Описаното явление се нарича резонанс, а съответната енергия - резонансна. Пиковете на сеченията при нискоенергетичните резонанси са много високи, а резонансните ширини (енергетичният интервал около пика, в който сечението надхвърля половината от пиковата си стойност) са много малки. Така например, пикът на при енергия на налитащия неутрон 6.67 eV е » 7 000 b (почти изцяло поради поглъщане). Тази величина е измерена при стайна температура, т.е. при съответното топлинно движение на ядрото-мишена. При неподвижна мишена пиковата стойност би била » 20 000 b, а ширината на резонанса - 0.027 eV. Поради топлинното движение на ядрото-мишена интервалът от енергии на налитащия неутрон, при които може да настъпи резонанс, се разширява, а пиковата стойност на сечението намалява (тъй като пълната вероятност (площта под пика) за резонансно взаимодействие, която е функция на свойствата на ядрото, остава една и съща). Това явление се нарича доплерово разширение на резонансите. Както обаче ще бъде показано по-нататък, в хетерогенна размножаваща среда, където има пространствено обособени области с делящ се материал и със забавител на неутрони, вероятността за поглъщане на неутрони от ²³⁸U нараства с разширяването на резонансните пикове, т.е. с увеличаване на температурата на горивото. Описаното явление, често наричано доплеров ефект, има решаващ принос за стабилността на реактора като обект за управление.

При енергии на неутроните над няколкостотин eV резонансните пикове на при тежките елементи стават все по-плитки и широки и се припокриват, така че експериментално измерената зависимост на от енергията E придобива плавен вид. Енергетичният диапазон от няколкостотин eV до няколко keV се нарича област на неразделените резонанси.

Над областта на неразделените резонанси сеченията за поглъщане както при тежките, така и при леките елементи имат широки плитки резонанси и са малки (няколко барна). При такива енергии в започват да имат принос реакции с изпускане на заредени частици, напр. (n,p).

Разсейването на нискоенергетични неутрони върху повечето ядра е еластично (със запазване на пълната механична енергия и импулс на системата неутрон-разсейващ център), а съответното сечение не зависи от енергията и е малко по порядък ( 10 b). Важно изключение от това правило е разсейването върху ядро, което е в химична връзка с други ядра или е част от кристална структура. При такива условия неутроните взаимодействуват с няколко ядра наведнъж, а разсейването често бива нееластично (част от кинетичната енергия на неутрона се поглъща от разсейващата система във вид на нейна вътрешна енергия). Особено важно следствие от този ефект е, че сеченията за разсейване на водорода в H₂O и на деутерия в D₂O нарастват значително с намаляването на енергията на налитащия неутрон. Сеченията за разсейване при леките и средно тежките елементи остават постоянни чак до MeV-овия диапазон, където може да се появят широки и плитки резонанси. При тежките елементи могат да се появят резонанси на разсейването, наред с резонансите на поглъщане, непосредствено над топлинната област.

За делящите се нуклиди сечението за делене в топлинната област следва зависимостта 1/v и е много голямо. Например (0.0253) = 582 b, а (0.0253) = 1009 b, докато (0.0253) = 0.332 b, (0.0253) = 0.18 b, (0.0253) = 2.53 b и (0.0253) = 2.73 b.

Над топлинната област (E > 1 eV) се появяват големи тесни резонанси. Те стават по-плитки и по-широки в keV-овата област. Във високоенергетичната област (keV-ове до MeV-ове) сечението за делене на делящите се нуклиди става почти постоянно и е от порядъка на барнове.

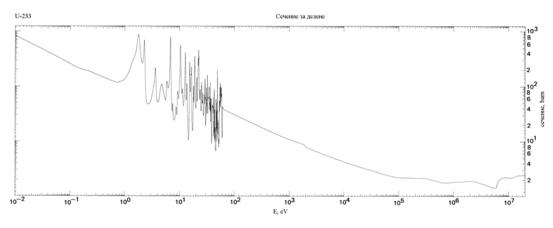
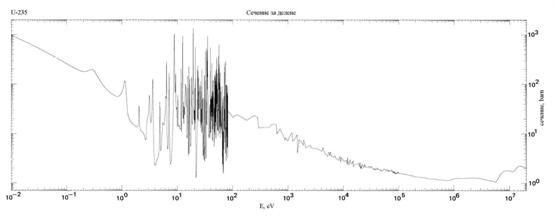
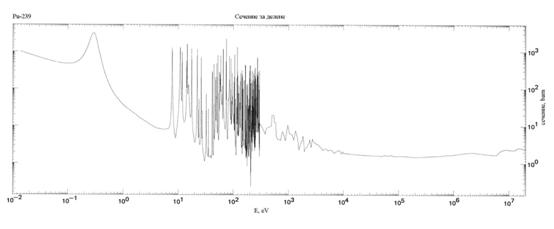
Делимите изотопи (²³⁸U, ²⁴⁰Pu, ²³²Th и др.) имат енергетични прагове около 1-2 MeV. Под тези прагове сеченията за делене са практически нулеви. Над праговете те нарастват бързо, но се стабилизират при стойност няколко барна.

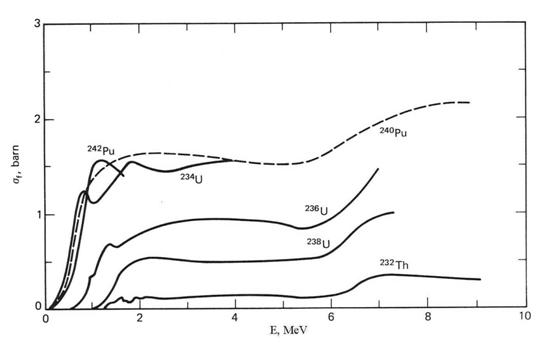
Скорости на неутронните реакции

Основната практическа задача на реакторния анализ се свежда до намирането на скоростите на различни видове неутронни реакции в пространствена област с произволни, но известни материален състав и размери. Наред с познаването на съответните микро- и макроскопични сечения за взаимодействие, решаването на тази задача изисква и определяне на характеристиките на съвкупността от свободни неутрони в разглежданата област. Най обща характеристика за тази цел е броят на неутроните във всеки диференциално малък обем dV около точката r, имащи кинетични енергии между E и E+dE и посоки на движение в диференциално малък пространствен ъгъл dW около единичния вектор W. Поради вероятностния характер на неутронните взаимодействия този брой ще бъде случайна величина, но доколкото концентрацията на свободни неутрони в ядрените реактори е висока (» 10⁸ неутрона/cm³), индивидуалните характеристики на отделните неутрони може да се заменят със статистически величини (средни стойности), отнасящи се до "неутронния газ". Основна величина в този случай е неутронната плътност N(r,W,E,t), определена по следния начин:

N(r,W,E,t)dVdEdW е средният (очакван) брой неутрони, които в момента t се намират в елементарния (безкрайно малък) обем dV, съдържащ точката с радиус-вектор r, имат енергия в елементарния интервал dE около E и се движат в посока, съдържаща се в елементарния конус от посоки dW около посоката W.

Описвайки по подходящ начин процесите на взаимодействие на неутронния газ с материалната среда, може да се състави уравнение относно неутронната плътност N(r,W,E,t). По-конкретно, ако запишем чрез математически израз твърдението, че скоростта на изменение на N(r,W,E,t) в момента t е разликата между скоростта на поява на неутрони във фазовия обем dVdEdW (поради възникването им в пространствения обем dV в резултат на делене, поради изменение на енергията или посоката на движение на неутроните след сблъсък с ядрата на атомите в пространствения обем dV, или поради пренос през околната повърхност на обема dV) и скоростта на напускане на неутрони от фазовия обем dVdEdW (поради поглъщане от ядрата на атомите в dV, поради изменение на енергията или посоката на движение на неутроните след сблъсък с ядрата на атомите в пространствения обем dV, или поради пренос през околната повърхност на dV), ще получим едно интегро-диференциално уравнение за N(r,W,E,t). Приложено за неутронния газ и споменатите по-горе процеси на взаимодействие на неутроните с веществото, то се нарича уравнение на неутронния пренос (УНП). При съставянето му се пренебрегват два процеса:

а) взаимодействието на неутроните помежду им, тъй като вероятността за това е нищожна поради малката плътност на неутронния газ (неутронният газ е много по-разреден от класическия газ, напр. въздуха, чиято концентрация е »10¹⁹ молекули/cm³), и

б) радиоактивното разпадане на неутрона, тъй като за неговото средно време на живот (15.3 мин.) вероятността той да остане във фазовия обем dVdEdW е практически равна на нула.

Решаването на уравнението на неутронния пренос би дало възможност за предсказване на поведението на ядрените реактори с точност, ограничена само от точността на основните ядрени данни, използувани за оценяване на вероятностите на различните видове взаимодействия на неутрон с дадена енергия с атом от дадено вещество, т.е. на ядрените сечения за неутронно взаимодействие.

За целите на практиката, след отчитане на точността, с която са известни материалните характеристики на средата (активната зона на реактора), ядрените данни, особеностите на енергетичната зависимост на сеченията, както и с оглед на нужните резултати от пресмятанията (коефициенти на неравномерност на енергоотделянето, дълбочина на изгаряне, критична концентрация на борната киселина, ефективност на ОР СУЗ, ефекти и коефициенти на реактивността и т.н.), УНП се модифицира и опростява така, че неговото решаване става възможно с разумни изчислителни разходи. Такива модифицирани и опростени форми на УНП се използуват за инженерни пресмятания в процеса на конструиране и на експлоатация на ядрените реактори. В частност, при експлоатацията на ЯР с помощта на такива пресмятания се избира схема на презареждане, определят се характеристиките на реактора като обект на управление, моделира се разпределението на енергоотделянето в активната зона и т.н.

Връщайки се към разгледания по повод на дефинирането на неутронните сечения пример, лесно може да се съобрази, че броят на неутроните, пресичащи за единица време елементарна площта на мишената dS е v(E)N(r,W,E,t)dWdEdS, където v(E) е модулът на скоростта на неутроните. Тъй като е вероятността един неутрон да предизвика взаимодействие a с нуклида j при изминаване на разстояние dx в материала на мишената, то очакваният брой взаимодействия от този вид за единица време в обем dV º dSdx е произведението на броя на неутроните, пресичащи за единица време перпендикулярната на dx площ dS и вероятността :

Произведението се среща много често в изрази от подобен вид, поради което за него е въведен специалният термин насочена (или ъглова) плътност на неутронния поток и означението .

Тъй като, с изключение на специалния случай на разсейването, който ще бъде разгледан по-нататък, в енергетичния диапазон на неутроните в ядрените реактори и за материалите от реакторната среда макроскопичните сечения за взаимодействие не зависят от измерваната в лабораторната координатна система посока на движение на неутроните W, пълната скорост на реакцията a във фазовия обем dVdE може да се пресметне чрез интегриране на насочената плътност на потока j(r,W,E,t) по всички посоки W: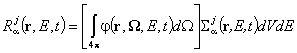

Величината се нарича плътност на скаларния поток, скаларен поток или просто поток.

Диференциални сечения за разсейване

Наред със скоростите на реакциите, за моделиране на поведението на неутроните в реактора е нужно да се знаят и енергиите и посоките на движение на неутроните след делене или разсейване. Тъй като освободените при делене неутрони се изпускат изотропно и независимо от посоката на движение на предизвикалия деленето неутрон, а енергетичният им спектър зависи от свойствата на делящото се ядро и практически не зависи от енергията на предизвикалия деленето неутрон, характеристиките на неутроните от делене се моделират просто. Следователно, основният проблем се състои в описване на пространствено- енергетичното разпределение на неутроните след разсейване.

Двойни диференциални сечения за разсейване

Аналогично на скоростите на останалите неутронни реакции, броят на актовете на разсейване (еластични и нееластични) за единица време между неутроните във фазовия обем dVdW’dE’ и веществото в dV ще се дава от израза: .

За определяне на пространствено-енергетичното разпределение на неутроните след разсейване са нужни още и, за всеки тип ядра j, вероятностите за еластично и нееластично разсейване от фазовия обем dW’dE’ във фазовия обем dWdE (т.е. промяна на енергията от E’ в E и на посоката на движение от W’ в W). Тези вероятности се наричат двойни диференциални сечения за разсейване и се определят по следния начин:

Вероятността неутрон с енергия E’ и посока на движение W’ в резултат на еластично (a = el) или нееластично (a = in) разсейване с ядро от тип j да придобие енергия в интервала dE и посока на движение в конуса dWе . Тъй като е плътност на вероятността, а при разсейване неутронът винаги придобива някаква енергия и посока на движение, то .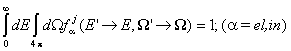

За по-нататъшните разглеждания ще бъде нужно да се въведат следните основни елементи от описанието на единичния вектор на посоката W в лабораторната координатна система. Координатите на този вектор се изразяват чрез ъгъла между W и оста Oz, и ъгъла j между проекцията на W в равнината Oxy и оста Ox. q се мени от 0 до p, а j - от 0 до 2p. Така W_x = sinqcosj; W_y = sinqsinj; W_z = cosq. dW има смисъл на площта от повърхността на единичната сфера, която върхът на W описва при нарастване на q с dq и на j - с dj: dW = sinqdjdq. Тъй като q се мени от 0 до p, то m º cosq е еднозначна функция на q и се мени от 1 до -1. Или: dW = -dmdj. Интегралът по всички възможни стойности на q и на j, т.е. площта на единичната сфера, ще бъде 4p.

В ядрения реактор неутроните взаимодействуват практически винаги с хаотично ориентирани частици. В този случай, при дадени начална и крайна енергии на неутрона, вероятността за разсейване от W’ в W зависи само от "ъгъла на разсейване" q между векторите W’ и W. Нека m₀ º cosq = W.W’. Това е z-координатата на W по единствената физически различима ос в пространството - посоката на движение на налитащия неутрон W’. Тогава двойната диференциална плътност на вероятността за разсейване ще бъде еднозначна функция на m₀: или , а нормировъчното условие ще бъде: 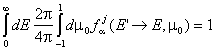. С помощта на и се определя двойното диференциално сечение за разсейване:

Единични диференциални вероятности за разсейване

В много приложни случаи е достатъчно да се знае само вероятността за промяна на енергията на разсеяния неутрон от E’ в Е или само вероятността за смяна на посоката на движение при разсейване от W’ в W:

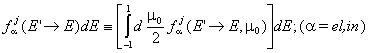, или

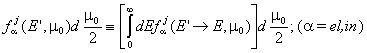
Вероятностите за разсейване обикновено се измерват и пресмятат не в лабораторната координатна система (ЛКС) (в която центърът на масата на реактора е в покой), а в системата на центъра на масите (СЦМ) (в която центърът на масите на неутрона и разсейващия център (ядро) е в покой), т.е. обикновено са известни , където m_c е косинусът на ъгъла на разсейване в СЦМ, а E и E' са кинетичните енергии в ЛКС.

При множество нуклиди и в широк диапазон на енергията на налитащия неутрон разсейването е изотропно в СЦМ, т.е. всички стойности на q_c са равновероятни. В тези случаи зависи само от началната и крайната енергия.

Аналогично на въвеждането на двойното диференциално сечение за разсейване се определят микроскопичните диференциални сечения:

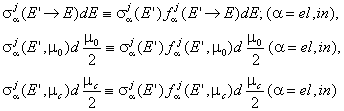
и макроскопичните диференциали сечения за разсейване:

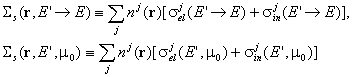, където n^j са ядрените обемни концентрации. Макроскопични сечения в СЦМ не могат да се дефинират, тъй като за всеки тип ядро j с маса A_j и за всяка различна енергия на неутрона E’ тази координатна система е различна.

Връзки между диференциалните вероятности за еластично разсейване

В случая на нееластично разсейване енергията E на разсеяния неутрон не е еднозначно свързана с косинуса на ъгъла на разсейване m₀ или m_c. Стойностите на или се определят в резултат на ядрено-физични експерименти и теоретични анализи. При еластичното разсейване има еднозначна връзка между промяната в енергията E’®E, m_c и m₀. В този случай необходимите ядрено-физични данни са само и (определянето на вероятния ъгъл на разсейване m_c изисква квантово-механични пресмятания и експерименти), а промяната в енергията на неутрона и m₀ се пресмятат съгласно законите на механиката. Входните предпоставки и резултатите от такъв, сравнително опростен, анализ са следните.

Приема се, че ядрото-мишена е в покой относно центъра на масата на реактора, т.е. в ЛКС. Това пренебрегване на топлинното движение на ядрото е допустимо при енергия на налитащия неутрон над областта на тесните резонанси (» 100 eV), а за леки ядра (без резонанси на сечението за разсейване) - за енергия на неутрона над около 1 eV. Приема се също така, че неутронът и ядрото са материални точки, т.е. без линейни размери. Отчитането на истинския механизъм на взаимодействие става чрез . Нека масата на ядрото-мишена е M_j , на неутрона - m, а A_j º M_j/m. Нека 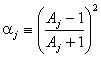. Тогава:

а) Минималната енергия на неутрона след еластично разсейване е E_min = a_jE’, а максималната енергия E_max = E’.

б) E’, E, и m_c са свързани еднозначно по следния начин: , а m₀ се определя от A_j и m_c: .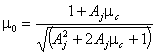

в) Връзката между диференциалните вероятности за разсейване е: . Ако разсейването е изотропно в СЦМ, то: .

Други често използувани резултати и величини, свързани с механичния анализ на разсейването, са:

1. Среден косинус на ъгъла на разсейване в ЛКС

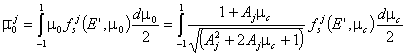
При изотропно разсейване в СЦМ , т.е. клони към нула за тежките ядра, а напр. за водорода е 2/3, което съответствува на среден ъгъл на разсейване 48.2°. Тук следва да се отбележи, че във всички случаи средният косинус е положителен, т.е. разсейването в ЛКС е винаги “напред”.

2. Средна логаритмична загуба на енергия x_j

За изотропно разсейване в СЦМ:

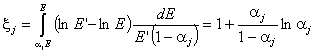
3. Летаргия u

Летаргията (u) е мярка за неутронната енергия, въведена за удобство при анализа на забавянето на неутроните. Точното определение на летаргията е: , където E е енергията на неутрона, а E₀ е някаква реперна (начална) стойност - напр. 10 или 15 MeV (практически най-високата енергия на един изпуснат в резултат на делене неутрон). Тъй като , то x_j е средното нарастване на летаргията на неутрона при разсейването му върху ядро от тип j.

4. Възраст на неутроните t(E)

За удобство на аналитичното моделиране на преносните явления в процеса на забавянето на неутроните от раждането им при делене до достигането на топлинно равновесие със средата се въвежда независимата променлива "възраст на неутрона", t(E). С нейна помощ уравнението на пренос на забавящите се неутрони придобива математичния вид на нестационарното уравнение на топлопроводност, в което възрастта изпълнява ролята на времето. Физичният смисъл на възрастта е следният. Ако в безкрайна еднородна неразмножаваща среда бъде поставен точков източник на неутрони с енергия E₀ (напр. 15 MeV), то възрастта t(E) ще бъде числено равна на една шеста част от средния квадрат на разстоянието по права линия, което неутронът изминава от мястото на източника до забавянето си до енергия E: . Ясно е, че при равни други условия възрастта ще бъде характеристика на забавящата способност на средата.