2. Забавяне на неутроните. Механизъм на забавяне в леки и тежки забавители. Неутронно-физични характеристики на забавителите - забавяща способност, коефициент на забавяне, изисквания към забавителите.

Връщайки се към приведеното в Глава 1 определение на средната логаритмична загуба на енергия при един акт на еластично разсейване x, и използувайки определението на въведената пак там величина a, може да се изведе следният приблизителен израз: . Той е достатъчно точен за A > 10, а даже за A=2 неговата относителна грешка е само 3.3%. Стойностите на x за някои чисти вещества са следните:

вещество	масово число	x	среден брой разсейващи удари за забавяне до топлинна енергия
водород	1	1.0	18
деутерий	2	0.725	25
хелий	4	0.425	43
литий	7	0.268	67
берилий	9	0.209	86
въглерод	12	0.158	114
кислород	16	0.120	150
уран	238	0.00838	2172

Средният брой разсейващи удари за забавяне до топлинна енергия се отнася за начална енергия на неутрона 2 MeV (средна за неутроните от делене) и крайна енергия 0.025 eV (съответствуваща на топлинно равновесие на неутронния газ със средата при температура 300 K) и е равен на

За оценяване на качеството на забавителя, наред със стойността на x е нужно да се отчита и вероятността за разсейване. Съвместна мярка на тези две количествени характеристики на разсейващата среда е тяхното произведение, xS_s, наричано макроскопична забавяща способност. Тъй като макроскопичното сечение за разсейване е , където N_A е числото на Авогадро, r е обемната плътност на забавителя, s_s е неговото ефективно микроскопично сечение за разсейване, а A е неговото атомно (или молекулно) тегло, забавящата способност е равна на .

Въпреки че забавящата способност е задоволителна характеристика на забавящите свойства на веществото, тя не описва напълно неговото качество като забавител в състава на ядрения реактор, защото не отчита възможността дадено вещество да бъде и силен поглътител на неутрони. Отношението на определената по-горе забавяща способност към макроскопичното сечение за поглъщане S_a, т.е. , наричано коефициент на забавяне, е от теоретична гледна точка най-важната количествена характеристика на ефективността на забавителя. Приблизителните стойности на тази величина за някои вещества, пресметната с помощта на сечението за поглъщане на топлинни неутрони, са:

забавител	забавяща способност, cm^-1	коефициент на забавяне
вода	1.53	72
тежка вода	0.37	12000
хелий	1.6.10^-5 (при нормално налягане и температура)	83
берилий	0.176	159
въглерод	0.064	170

От приведените в таблицата стойности се вижда, че обикновената вода, използувана за забавител в реакторите ВВЕР, както и във всички леководни реактори, е далече не най-добрият избор от неутронно-физична гледна точка. Изборът на забавител в ядрените реактори обаче се диктува и от редица други физични, технически и икономически изисквания. По принцип, идеалният забавител трябва да бъде с висока плътност, химически стабилен, с много ниско атомно тегло и сечение за поглъщане на неутрони, с много висока точка на кипене и, не на последно място, достатъчно достъпен. Тези изисквания се удовлетворяват, макар и в различна степен, от графита, обикновената вода или тежката вода, използувани в качеството на забавители в съвременните реактори. Графитът е относително евтин, има много ниско сечение за поглъщане на неутрони (0.0034 b при 0.025 eV), но е със слаба забавяща способност (маса 12 а.е.м.), поради което реакторът с такъв забавител има много големи размери. Най-често използуваният забавител в енергетичните реактори е обикновената вода, служеща едновременно и за топлоносител. Водородът във водата е с най-висока забавяща способност, но поради относително голямото си сечение за поглъщане на неутрони (0.025 eV) = 0.332 b има нисък коефициент на забавяне. Освен това, точката на кипене на водата е ниска, така че активната зона трябва да бъде затворена в корпус под високо налягане. Тъй като сечението за поглъщане на топлинни неутрони на деутерия е много по-ниско, тежката вода се използува за забавител в реакторите с природен (0.7% ²³⁵U) или съвсем слабо обогатен уран. При тежката вода главният проблем е изключително високата й цена.

Забавяне в безкрайна среда

Нека предположим, че равномерно в обема на дадена забавяща среда с определена скорост се генерират, напр. в резултат на делене, бързи неутрони. В хода на своето взаимодействие с ядрата на забавителя тези неутрони постепенно губят енергия, но доколкото едновременно с това непрекъснато се генерират нови бързи неутрони, в забавящата среда се установява стационарно енергетично разпределение на неутроните. Ако допълнително предположим, че средата е безкрайна, т.е. пренебрегнем утечката на неутрони през нейните граници, това енергетично разпределение няма да зависи от координатите. За опростяване на разглежданията ще приемем, че разсейването е сферично симетрично относно центъра на масите на системата неутрон-ядро, и че ядрата-мишени са неподвижни в лабораторната координатна система. Последното допускане е справедливо за енергия на неутроните над около 1 eV, т.е. много по-голяма от енергията на топлинното движение на ядрата.

При така дефинираните условия може да се състави следното уравнение за неутронния баланс (или уравнение на забавянето) в енергетичния интервал dE около всяка произволна, но фиксирана енергия Е:

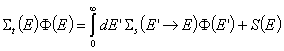
Лявата страна е скоростта на извеждане на неутрони от dE поради разсейване или поглъщане. Първият член отдясно е скоростта на поява на неутрони в dE поради промяна на енергията на разсеялите се неутрони, а вторият член е скоростта на поява на неутрони в dE от независимия източник S(E), cm^-3s^-1, напр. от делене.

На практика това уравнение може да опише реалния спектър на бързите неутрони достатъчно добре, тъй като в голям енергетичен реактор краевите ефекти, т.е. утечките, имат малък принос в неутронния баланс. Освен това, при бързите неутрони пространствените ефекти, дължащи се на хетерогенността на активната зона, са също слабо изразени, защото в тази енергетична област вариацията на сеченията е относително малка, а дължините на свободен пробег на неутроните са големи.

При направеното по-горе допускане за процеса на разсейване и съгласно разглежданията в Глава 1, сечението за разсейване ще има вида: .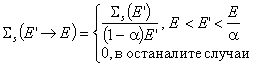

Забавяне във водород при пренебрегване на поглъщането

За получаване на прости аналитични решения на балансното уравнение най-напред ще приемем, че веществото на забавителя е водород (A=1, a=0) и че отсъствува поглъщане. Последното допускане не е твърде грубо, защото . В този случай уравнението на забавянето придобива вида: 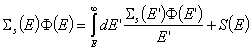. Избраната долна граница на интегриране отчита обстоятелството, че бързите неутрони не могат да увеличават енергията си след разсейване.

Въвеждайки нова зависима променлива , наречена плътност на разсейващите удари, и приемайки, че източникът на неутрони е моноенергетичен с енергия Е₀ и интензитет S₀, уравнението на забавянето се записва по следния начин: 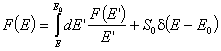, където d е делта-функцията на Дирак.

Отбелязвайки, че поради сингулярния източник решението F(E) трябва да съдържа член, пропорционален на , ще го търсим във вида: . След заместване в уравнението на забавяне се получава:

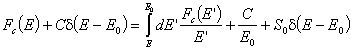. (Вторият член отдясно е поради следното свойство на делта-функцията: .) Тъй като сингулярните членове трябва да бъдат равни помежду си, е нужно константата C да бъде равна на S₀, т.е.:.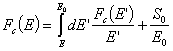

Не е трудно да се съобрази, че F_c(E) удовлетворява уравнение, в което ролята на неутронен източник S(E) изпълняват неутроните, претърпели еднократно разсейване при енергията на действителния източник E₀.

Действително, при a = 0. В този смисъл сингулярната компонента на F(E), , е просто приносът на неутроните, които не са претърпели нито едно разсейване и имат първоначалната енергия E₀.

Решаването на интегралното уравнение за F_c(E) може да стане след преобразуването му в обикновено диференциално уравнение:

.

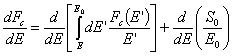Или, прилагайки правилото за диференциране на определен интеграл, : .

Общото решение на това уравнение е . За определяне на константата C се използува началното условие при E = E₀, следващо пряко от интегралното уравнение: . Следователно, C = S₀, а пълното решение на уравнението на забавянето е: , или: .

Тъй като сечението за разсейване на бързи неутрони зависи слабо от енергията, от горното следва, че спектърът на забавящите се неутрони е приблизително пропорционален на 1/E. Това твърдение е още по-обосновано в относително тесни енергетични диапазони.

Решението на уравнението на забавяне при произволен спектър на източника S(E) се получава по аналогичен на разгледания по-горе начин: .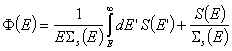

За целите на по-нататъшния анализ е целесъобразно да се въведе величината плътност на забавянето q(E), която се определя по следния начин:

q(r,E)dV º брой на неутроните в обема dV  около точката r, забавящи се под дадена енергия E.

Или, количествено изразено чрез скоростта на реакцията на разсейване: .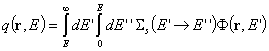

За разглежданата дотук безкрайна водородна непоглъщаща среда:

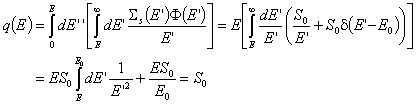
Следователно, както и трябва да се очаква при липса на поглъщане и утечки, плътността на забавяне е постоянна и равна на интензитета на източника - т.е. всички неутрони от източника неизбежно ще се забавят под всяка енергия E.

Най-удобна независима променлива при анализа на спектъра на бързите неутрони е летаргията, защото съгласно нейното определение . Така в много изрази автоматично се елиминират често срещащите се множители 1/E. Например, доколкото летаргията е еднозначна функция на енергията, за плътността на разсейващите удари е в сила: , или . Следователно, в разглеждания дотук конкретен случай и при E ¹ E₀, т.е. u > 0, F(u) = S₀. В по-общите случаи се оказва, че F е много по-слабо варираща функция на летаргията u, отколкото на енергията E.

Втори пример е дефинирането на диференциалната вероятност за еластично разсейване . От основното равенство следва, че: . Също така, от следва, че . Уравнението на забавяне, записано чрез летаргията, е: 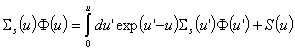. Плътността на забавяне, записана чрез летаргията, е: 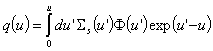. Диференцирането на този израз по u дава: 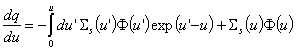, или: .

Както ще стане ясно по-нататък, получената връзка между плътността на забавяне и спектъра, изразени чрез летаргията, ще доведе до значително опростяване на математичния апарат при анализа на енергетичното и пространственото разпределение на неутроните в реакторната среда.

Забавяне във водород с отчитане на поглъщането

Физичната ситуация в този случай може да отговаря напр. на забавяне в смес от ядра на силно поглъщащ нуклид като ²³⁸U и ядра на водорода, чието сечение за поглъщане е в действителност пренебрежимо малко. За простота може да се приеме, че поглъщащият нуклид е “безкрайно тежък” и не забавя неутроните, така че забавянето отново става чрез разсейване в ядра с масово число A = 1. В този случай решението на уравнението на забавяне отново ще има вида , където: 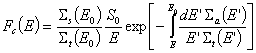. Вижда се, че при S_a=0 този израз преминава в получения по-горе за среда без поглъщане. Плътността на забавяне при наличие на поглъщане е: .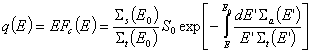

Тъй като S₀ е скоростта на възникване на неутроните с начална енергия E₀ от източника, а q(E) е скоростта на забавяне на неутроните под енергия E, то има смисъл на вероятността изпуснат от източника неутрон да не бъде погълнат в процеса на забавяне до енергия E.

Забавяне във вещество с масово число A > 1 при пренебрегване на поглъщането

При моноенергетичен източник с енергия E₀ уравнението на забавяне, записано за неутроните, претърпели еднократно разсейване, е:

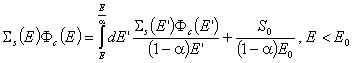
Разликата спрямо случая A=1 е в това, че до енергия E могат да достигнат неутрони, които преди разсейващия удар са имали енергия не повече от E/a.

Записвайки уравнението на забавяне относно плътността на разсейващите удари и диференцирайки по E се получава: . Тъй като първият член отдясно зависи от E/a вместо от Е, това уравнение изисква специфични методи за решаване. Допълнително усложнение е обстоятелството, че неговото решение F_c(E) е прекъснато (или има прекъснати производни) при енергии , съответствуващи на минималната енергия, до която неутронът може да се забави след n разсейващи удара. От друга страна, при енергии много по-ниски от тази на източника непрекъснатостта практически ще изчезне и F_c(E) ще придобие асимптотичния вид . В действителност това асимптотично поведение се оказва достатъчно точно за целите на повечето анализи, тъй като забавянето протича или предимно чрез разсейване във водородни ядра (в леководните реактори), при което не възниква непрекъснатост на спектъра, или пък се търси неутронният спектър при енергии много под енергията на източника.

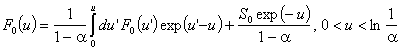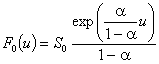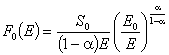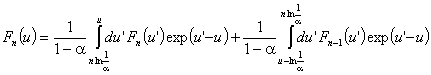Преминавайки към летаргия и разглеждайки само интервала , в който могат да попаднат неутроните след първия разсейващ удар, уравнението на забавяне придобива вида: . Диференцирането на това уравнение води до: при начално условие . Неговото решение е: , или . За плътността на разсейващите удари в интервала може да се запише: . След диференциране: . Решението на това уравнение е: 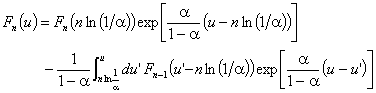. Знаейки F₀(u), получената рекурентна връзка може да се използува за пресмятане на F_n(u) при произволно n. Например: 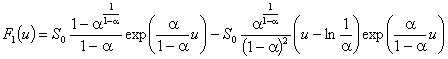. Както се вижда, при между F₀(u) и F₁(u) има прекъсване: . С нарастване на броя разсейващи удари n функциите F_n(u), наричани функции на Плачек, стават все по-гладки, а прекъсванията между тях постепенно изчезват. В действителност, за може да се получи асимптотично решение чрез пренебрегване на източника в уравнението на забавяне на неутроните, претърпели един разсейващ удар: . Лесно може да се провери, че F_c(u) = const. = C. По-нататъшният анализ показва, че в разглеждания случай на липса на поглъщане, , където x е средната логаритмична загуба на енергия (или средното нарастване на летаргията) при един разсейващ удар. Следователно, асимптотичният спектър на забавящите се неутрони (далече под енергията на източника) ще бъде: , или . Този извод може да се обобщи и за среда, представляваща хомогенна смес от различни нуклиди: , където .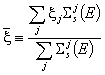

Забавяне във вещество с масово число A > 1 с отчитане на поглъщането

Уравнението на забавяне в този най-общ случай е:

, или:

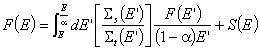. Множителят под интеграла прави аналитичното решаване на това уравнение практически невъзможно, освен в специалните случаи на подходяща енергетична зависимост на сеченията. Добавяйки обстоятелството, че при високи енергии нееластичното разсейване често е преобладаващ механизъм за забавяне, а също така и резонансната природа на сеченията при надтоплинни енергии, за решаване на уравнението на забавяне обикновено се предпочитат числени методи.

Във всички случаи, обаче, се потвърждава направеното в началото на тази глава твърдение, че в не много широки енергетични диапазони спектърът на забавящите се неутрони следва приблизително зависимостта .

Анализът на пространствено-енергетичното разпределение в крайна среда ще бъде направен в следващите глави.