3. Неутронен пренос. Елементарна теория на дифузията, уравнение на дифузията, дифузионни характеристики на преносните среди. Пространствено и енергетично разпределение на неутроните в процеса на забавяне. Възрастово приближение.

Уравнение на неутронния пренос

Наред с въведените в Глава 1 по повод на скоростите на неутронните реакции величини неутронна плътност N(r,W,E,t), насочена плътност на неутронния поток и плътност на скаларния поток , за целите на по-нататъшните разглеждания е нужно да се въведат и следните две величини:

Насочена плътност на неутронния ток, , със следната физична интерпретация: брой неутрони с енергия в интервала dE около E, които в момента t пресичат повърхнина с елементарна площ dS около точката r, движейки се в конуса от посоки dW около посоката W. (Тук dS = e_sdS, където e_s е единичен вектор, насочен по външната нормала на повърхнината dS)

Плътност на неутронния ток (или просто неутронен ток), . От определението следва, че физичната интерпретация на плътността на неутронния ток е: резултантен брой неутрони с енергия в интервала dE около E, които в момента t пресичат “отвътре навън” повърхнина с елементарна площ dS около точката r. (Ако този брой е отрицателен, това означава, че резултантният пренос през dS е “отвън навътре”.

Уравнението на неутронния пренос се записва относно насочената плътност на потока и е математичен израз на баланса на различните механизми, по които неутроните с дадена енергия и посока на движение могат да възникват или да изчезват от произволен геометричен обем V. Броят неутрони в разглеждания обем, имащи енергия в интервала dE около E и посоки на движение в конуса dW около W, е . Ако обемът V не се мени с времето, скоростта на промяна на този брой ще се изразява чрез следното балансно уравнение:

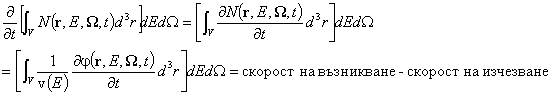
Механизмите на възникване и изчезване на неутрони от обема V могат да се класифицират както следва:

Механизми на възникване:

1 От неутронен източник във V (напр. от делене);

2 От втичане на неутрони през околната повърхност S на обема V;

3 Поради разсейване във V на неутрони с различни енергии E’ и посоки на движение W’, в резултат на което те придобиват енергия в интервала dE около E и посока на движение в конуса dW около W.

Механизми на изчезване:

4 От изтичане на неутрони през околната повърхност S на обема V;

5 От взаимодействия на неутроните с ядрата във V (водещи до поглъщане или до разсейване, съпроводено с промяна на енергията и посоката на движение)

По-долу ще бъдат получени математични изрази за всеки от тези механизми.

1 Неутронен източник. Ако се въведе следното общо определение, скорост на поява на неутрони от източника в обема d³r около точката r с енергия в интервала dE около E и посоки на движение в конуса dW около W, то 1 = .

5 Загуба от взаимодействия. От разглежданията в предходните глави е ясно, че 5 = .

3 Възникване поради разсейване. От предходните глави следва, че 3 = .

4-2 Резултантна загуба поради утечка. От определението за насочена плътност на неутронния ток следва, че 4-2 = . Съгласно теоремата на Гаус-Остроградски , този израз може да се запише във вида: 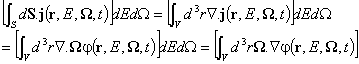. (Последното равенство е поради факта, че W и r са взаимно независими.)

След комбиниране на горните изрази се получава следният общ запис на балансното уравнение за обема V:

.

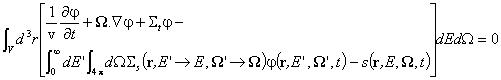Тъй като обемът V е произволно избран, горното равенство ще бъде винаги в сила само ако подинтегралната функция е тъждествено равна на нула:

.

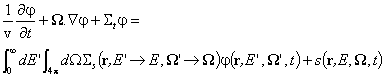Това е окончателният общ вид на уравнението на неутронния пренос при произволен източник. Ако се отчете фактът, че в ядрените реактори като правило този източник е единствено от верижната реакция на делене, и ако се пренебрегнат закъсняващите неутрони, то: .

Интегро-диференциалното уравнение на неутронния пренос ще има еднозначно определено решение единствено при подходящо дефинирани начални и гранични условия. Типично начално условие е за всяка стойност на r, E и W, като е отнапред известна функция. Едно от възможните гранични условия е т.нар. “условие на свободна повърхност”, базирано на обстоятелството, че ако обемът V е изпъкнал и извън него практически не протичат реакции на разсейване и делене (напр. включва изцяло активната зона и отражателя на един ядрен реактор) то напусналите този обем неутрони не могат да навлязат обратно в него, т.е. за всички точки r_s от околната повърхност S на обема V, ако

Преди да се премине към разглеждане на т.нар. дифузионно приближение на уравнението на неутронния пренос, е уместно да се направи общ преглед на методите за пряко числено решаване на това уравнение. Възможни са два принципно различни типа подходи, които често се прилагат в комбинация. Първият се състои в дискретизация на непрекъснатите независими променливи, а вторият - в разлагане на търсеното решение или на негови компоненти по набор от базови функции. За тяхното илюстриране ще разгледаме следното интегро-диференциално уравнение за функция на една променлива:

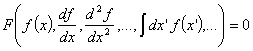
Дискретизацията се свежда до представяне на f(x) при краен набор от стойности x_i на независимата променлива x: . Производните се представят чрез крайни разлики, напр. . Интегралите се пресмятат по числени квадратурни формули от типа , където w_i са т.нар. квадратурни тегла. Така първоначалното уравнение се свежда до система от линейни алгебрични уравнения относно f_i, която се решава числено.

Разлагането по базови функции се състои в представянето: , където f_l са подлежащи на определяне коефициенти, а p_l(x) са предварително избраните и известни базови функции. Типичен начин за съставяне на система от уравнения за коефициентите f_l е чрез заместване на разложеното по базови функции търсено решение f(x) в първоначалното уравнение, последователно умножаване по всяка от базовите функции p_l(x), интегриране по независимата променлива x и използуване на някои специални свойства на p_l(x), като напр. ортогоналност. Крайният резултат е замяна на първоначалното уравнение със система от L по-прости и подходящи за числено или аналитично решаване уравнения. Като правило броят на тези уравнения е относително малък.

Изборът на подход и начинът на неговото прилагане са специфични за всяка от независимите променливи в уравнението на неутронния пренос.

Зависимост от посоката на движение W

Пряката дискретизация по W води до т.нар. метод на дискретните ординати, съгласно който тази независима променлива се представя чрез набор от посоки W_n, n = 1,...,N. Функциите на W се представят чрез своите стойности във всяка от дефинираните посоки: . Така интегрирането се свежда до сумиране, , където w_n са подходящо избрани квадратурни тегла, осигуряващи достатъчно точно апроксимиране на интеграла. Уравнението на неутронния пренос се свежда до система от N уравнения (т.нар. S_N уравнения) от вида:

,

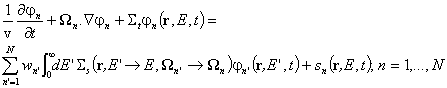където .

При алтернативния метод на разлагането по базови функции насочената плътност на потока се представя най-често чрез познатите от квантовата механика сферични хармоники : . След заместване на това представяне в уравнението на неутронния пренос, умножаване по сферични хармоники от различен ред, , интегриране по W и използуване на тяхната ортогоналност, се получава система от уравнения за коефициентите на разложението .

Така например, в едномерния случай разлагането по сферични хармоники съответствува на разлагане по полиноми на Лежандър , където , а q е единствената физически различима компонента на векторa W в сферични координати (): . За системата от уравнения за коефициентите на разложението , или т.нар. P_L уравнения, се получава:

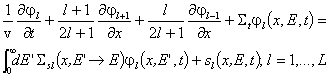,където и .

Тук е уместно да се отбележи, че докато P₁ уравненията (тясно свързани с дифузионното приближение на уравнението на неутронния пренос) се използуват често при решаване на задачи на реакторния анализ, до P_L уравненията от по-висок ред се прибягва много рядко. За детайлно моделиране на насочената плътност на потока, когато това е необходимо, се прилага методът на дискретните ординати.

Зависимост от енергията E

За описването на тази зависимост методът на разлагане по базови функции не се прилага, тъй като за да бъде той ефективен е нужно тези функции да наподобяват действителната зависимост на неутронния поток от съответната независима променлива. Зависимостта на насочената плътност на потока от посоката W е обикновено относително слаба, поради което набор от стандартни функции, като напр. сферичните хармоники, осигурява достатъчно добро приближение за нея даже при нисък ред на разложението. Неутронните енергии E, обаче, заемат стойности в огромния диапазон от 10^-3 eV до 10⁷ eV, а зависимостта на неутронния поток от енергията се определя от твърде различни процеси в различните енергетични диапазони. При високи енергии неутронният спектър наподобява на спектъра на неутроните от делене, при междинни енергии доминиращи процеси са забавянето и резонансното поглъщане, а при ниски енергии спектърът се определя от неутронната термализация. Практически невъзможно е да се намерят базови функции, които да апроксимират достатъчно добре всичките тези процеси.

Прилагането на метода на дискретизация спрямо енергетичната променлива също не може да бъде директно поради сложната зависимост на неутронните сечения от енергията. Тяхното табулиране в разумен брой точки по енергия не може да осигури достатъчно добро представяне на действителната им енергетична зависимост. Общоприетото в случая решение е да се разбие пълният енергетичен диапазон на интервали, наричани неутронни групи и номерирани в посока на намаляване на енергията. Уравнението на неутронния пренос (или дифузионното уравнение) се интегрира по всяка група с цел дефиниране на подходящи групови средни стойности на различните неутронни сечения. Например, дефиницията за сечението за поглъщане в група g е:

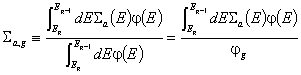, където j_g е потокът в група g. Естествено, тези определения са формални, защото в тях участвува търсеният поток, но те представляват реална основа за практически приложения, тъй като за пресмятане на груповите сечения могат да се използуват подходящи приближения на потока.

Прилагайки описаната схема към вече въведените S_N уравнения, се получава следната система от многогрупови уравнения за груповите потоци :

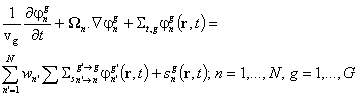
Зависимост от координатите r и времето t

За отчитане на тези зависимости разлагането по базови функции по принцип е приложимо, но на практика се използува рядко и само в специални случаи. Общоприетият подход е пряката дискретизация със заместване на съответните производни с подходящи крайни разлики. Структурата на мрежите на дискретизация и диференчните формули (диференчен означава “на крайните разлики”) се избират съобразно вида на задачата.

Решаване на получените системи от уравнения

Прилагането на очертаните по-горе схеми спрямо уравнението на неутронния пренос води до появата на изключително големи системи от алгебрични уравнения за компонентите на представянето на потока, напр. . По принцип такива системи могат да се решават с помощта на стандартни числени методи, но огромните необходими изчислителни разходи на практика винаги изискват въвеждането на подходящи за типа на решаваната задача и физично обосновани опростявания и приближения. Така например, при мрежа на пространствено разбиване 100x100x100 точки, 10 енергетични групи и 10 дискретни направления, за всяка стъпка във времето ще бъде нужно да се реши система от 10⁸ алгебрични уравнения. Най-типичните приближения се състоят в пренебрегване на времето при моделиране на стационарни процеси или формулиране на т.нар. условно-критични задачи, опростено едно- или двумерно представяне на реакторната геометрия, елиминиране на ъгловата променлива W. Последното приближение е особено целесъобразно в широк клас от случаи, като най-често прилаганият за целта подход е въвеждането на т.нар. дифузионно приближение на уравнението на неутронния пренос, чието обосноваване ще бъде разгледано по-долу.

Дифузионно приближение на уравнението на неутронния пренос

От гледна точка на експлоатационните неутронно-физични реакторни пресмятания намирането на насочената плътност на потока в реакторната среда като решение на уравнението на неутронния пренос е в действителност само предпоставка за получаване на основния практически резултат от тези пресмятания - пространственото разпределение на скоростта на делене в активната зона на реактора, . Зависимостта на сечението за делене от времето се дължи главно на изменението на изотопния състав на горивото в хода на работата на реактора. Тъй като това изменение е бавно, за дадено състояние на активната то да се пренебрегне, а ако реакторът е критичен, т.е. има точно равенство между скоростта на генерация и скоростта на загуба на неутрони в активната зона, неутронният поток действително също няма да зависи от времето. Тук е уместно да се припомни, че поради съображения, изтъкнати в Глава 1, макроскопичните сечения за неутронните реакции с реакторните материали не зависят от посоката на движение на неутроните W. Познавайки скоростта на делене и скоростта на поглъщане , лесно могат да се пресметнат главните експлоатационни неутронно-физични характеристики на активната зона: разпределението на енергоотделянето и на дълбочината на изгаряне. Впрочем, за пресмятане на критичната борна концентрация и/или положение на ОР СУЗ, продължителността на кампанията, реактивностните ефекти и коефициенти и т.н. също е достатъчно познаването само на скаларната плътност на потока в нужните състояния на активната зона и моменти от кампанията (естествено, наред със съответните макроскопични сечения). Следователно, задачите на експлоатационния реакторен анализ биха се опростили значително, ако би било възможно на основата на уравнението на неутронния пренос да се състави уравнение за скаларния поток в активната зона на реактора.

Опитът за съставяне на такова уравнение може да започне с интегриране на уравнението на неутронния пренос по W. Без нарушаване на общността на по-нататъшните разглеждания, още тук е уместно да се направят следните допускания:

а) Съгласно казаното по-горе, зависимостта от времето се пренебрегва;

б) Източникът на неутрони се дължи на верижната реакция на делене (с пренебрегване на закъсняващите неутрони, което е напълно оправдано в контекста на предходното допускане), т.е. .

Интегрираното по W уравнение на неутронния пренос е:

Резултатите за отделните членове са:

[2] = ;

[4] = ;

[3] = , където

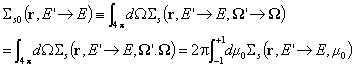
[1] = 

Или:

Полученото уравнение не може да се реши самостоятелно, тъй като съдържа две неизвестни функции, скаларния поток F и неутронния ток J, които, както следва от техните определения, не могат да бъдат получени една от друга.

Търсейки второ уравнение за F и J, интегрираме уравнението на неутронния пренос след неговото почленно умножаване по W:

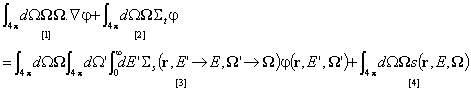
Резултатите за отделните членове са:

[2] = ;

[4] = , защото ;

[3] = , където

[1] = , където новата неизвестна функция P е тензор, в общия случай неприводим към F и/или J.

За да не се добавя уравнение за новата неизвестна функция (впрочем, при това ще се появи още една неизвестна функция и т.н., до образуването на безкрайна система), е нужно да се направи някакво опростяващо предположение за зависимостта на насочената плътност на потока от W. Най-подходящо в случая е да се приеме линейна зависимост, а именно:

, където и са подлежащи на определяне скаларна и векторна функции. От изискването дефинираният приблизителен израз да удовлетворява определенията за скаларен поток и неутронен ток следва, че и , или: . Заместването на този израз в [2] води до: [2] = .

Така се получава следната система от уравнения за F и J:

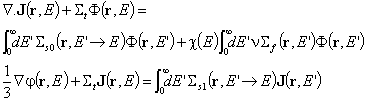
Тук е важно да се отбележи, че същата система би се получила в рамките на P_L приближението при L=1, и да се напомни, че единственото направено дотук допускане беше за слабата, и по-точно линейна, анизотропия на насочената плътност на потока. Тъй като второто от P₁ уравненията е векторно, интегро-диференциалните уравнения в системата са в действителност четири. В този смисъл задачата за намиране на скаларната плътност на потока би се опростила изключително много, ако второто от P₁ уравненията би могло да се използува за елиминиране на тока . В общия случай това , обаче, може да стане само чрез въвеждането на допълнителното допускане, че:

Това допускане би било обосновано, ако скоростта на разсейване на неутрони до дадена енергия е приблизително равна на скоростта на разсейване от тази енергия към всички други, напр. поради пренебрежимо малко поглъщане. При бързите неутрони действително процесите на разсейване преобладават над процесите на поглъщане, така че последните в относителен смисъл могат да се пренебрегнат. Подходящи доводи в полза на въвеждане на горното равенство могат да се изтъкнат и при топлинните неутрони.

Връщайки се към определението за се вижда, че тази величина може да се интерпретира като , тъй като 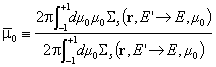има смисъл на среден косинус на ъгъла на разсейване.

Основавайки се на направеното допускане и въвеждайки т.нар. транспортно сечение , от второто от P₁ уравненията се получава:

Прието е величината да се нарича коефициент на дифузия, а връзката - закон на Фик. Тук е уместно да се напомни, че първото от P₁ уравненията беше получено без никакви приближения и няма ограничения за неговата приложимост, а законът на Фик е еквивалентен запис на второто от P₁ уравненията, след като в него бяха направени описаните по-горе две приближения, първото от които беше за линейна анизотропия на насочената плътност на потока.

Законът на Фик е математичен израз на твърдението, че преносът на неутрони става по посока на максималното намаляване на неутронната плътност и е пропорционален на големината на това намаляване за единица разстояние. И действително, при почти изотропен поток би следвало да се очаква преносът да бъде от области с висока плътност на разсейване към такива с по-ниска.

Законът на Фик е лошо приближение, когато насочената плътност на неутронния поток има силно изразен максимум в някаква определена посока (т.е. е силно анизотропна). Това може да се случи в близост до границата между две среди със силно различаващи се сечения за разсейване или поглъщане. Анализът на подобни ситуации показва, че законът на Фик е в сила на разстояние не по-малко от няколко дължини на разсейване (1/S_s) от такива граници - в области, където S_s(r,E) и S_a(r,E) не се изменят бързо като функция на координатите r и където S_s(r,E) >> S_a(r,E). Допусканията, при които е в сила този закон, не са валидни близо до външната повърхнина на реактора и близо до (или във вътрешността на) силни поглътители.

Използувайки закона на Фик в първото от P₁ уравненията, се получава т.нар. дифузионно приближение на уравнението на неутронния пренос:

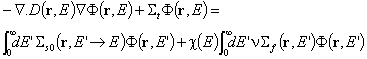
Тъй като единственото допускане при неговото съставяне е законът на Фик, може да се очаква, че то ще дава точни стойности за (r,E) в слабо поглъщащи среди на разстояние няколко дължини на разсейване от външна граница или силен поглътител на неутрони. Освен това, ако реакторът се състои от няколко пространствени области (например няколко еднородни горивни зони с различни обогатявания, оградени от отражател) и ако дифузионното уравнение е в сила за всяка зона поотделно, при подходящи гранични условия между тях то ще бъде в сила и за целия реактор.

За единственост на решението на дифузионното уравнение е нужно да се дефинират подходящи гранични условия за скаларния поток (r,E). Поради приближението, въведено чрез закона на Фик, са нужни и т.нар. вътрешни гранични условия, които ще бъдат разгледани най-напред.

Дифузионното уравнение е интегро-диференциално уравнение по трите пространствени координати и енергията. Коефициентите в него (D, S_t, nS_f и т.н.) са функции на координатите и енергията и могат да бъдат прекъснати по всяка от тези променливи. Възможните прекъсвания по енергия не създават математически проблеми, тъй като няма производни по енергия, а интегрирането на прекъснати функции е естествена процедура.

По-сложна е ситуацията по отношение на пространствените променливи. Дифузионното уравнението е частно диференциално уравнение от втори ред спрямо координатите, и за да има смисъл е нужно F(r,E) и трите компоненти на вектора да бъдат диференцируеми. Затрудненията, свързани с възможната прекъснатост на дифузионния коефициент, се заобикалят чрез налагане на вътрешни гранични условия за решението на дифузионното уравнение, основани на физичния смисъл на скаларния поток и на тока. Тъй като F(r,E)=v(E)N(r,E), а неутронната плътност трябва да бъде непрекъсната функция на координатите, то и F(r,E) трябва да бъде непрекъсната функция на r в целия реактор. Именно това е първото гранично условие. Второто гранично условие се състои в изискването за непрекъснатост на компонентата n.J(r,E) на неутронния ток през всяка вътрешна повърхност, разделяща два различни материала (единичният вектор n е нормален на тази повърхност). Физичният смисъл на това изискване е, че при пресичане на границата нито се губят, нито възникват неутрони. Ако се приеме законът на Фик, това означава, че трябва да бъде непрекъснато по направлението на n във всяка точка r на разделителната повърхност между двете среди. Естествено е, че в еднородна среда всеки вътрешен повърхностен елемент dS може да се разглежда като граница между две среди, които в този частен случай са еднакви.

Предпоставка за дефинирането на външни гранични условия е определянето на границата на реактора, което е в известен смисъл произволно. В съгласие с казаното по повод на граничните условия за уравнението на неутронния пренос, външната граница трябва да бъде такава повърхност, че никой от напусналите през нея неутрони да не може да се върне обратно. Ако реакторът би бил окръжен от вакуум или чисто поглъщаща среда (и е с изпъкнала форма), външната му граница би съвпадала с границата с вакуума или чистия поглътител. На практика реакторите винаги са оградени от разсейваща среда, която връща обратно част от изтичащите навън неутрони. Поради това външната граница се определя като най-малката окръжаваща реактора повърхнина, такава че връщащите се през нея неутрони да имат "пренебрежимо малък" ефект върху критичността на реактора и пространствено-енергетичното разпределение на потока във вътрешността му. Тъй като активните зони на почти всички реактори са оградени с отражател от неразмножаващ материал, обикновено за външна граница се приема повърхността на отражателя. Там (r,E) има много малка стойност и продължава да намалява експоненциално извън отражателя. Поради това ефектът върху критичността и разпределението на потока от обратно разсеяни извън отражателя неутрони е пренебрежимо малък. Следователно най-често прилаганото външно гранично условие за потока е: F(r,E)=0 за r на външната граница на отражателя. При експлоатационните неутронно-физични реакторни пресмятания обикновено дифузионното уравнение се решава само за горивната област. В този случай на границата между горивната област и отражателя (както и между горивните касети и поглътителите на ОР СУЗ във ВВЕР-440) се налагат външни гранични условия от типа: за r на съответната граница. Величината d(r,E) се нарича дължина на екстраполация и се пресмята чрез точно решаване на уравнението на неутронния пренос за типични състояния на реактора. Използуването й в дифузионното уравнение при експлоатационни пресмятания се основава на предположението, че по отношение на нейната стойност конкретното състояние на реактора не се различава съществено от типичното състояние, за което е била предварително пресметната.

Приблизителен израз за дължината на екстраполация може да се получи и чрез замяна на точното гранично условие на свободна повърхност за насочената плътност на потока, , с изискването резултантният ток, насочен навътре през границата на реактора да бъде нула, т.е.:

(Крайният резултат е получен по при приемане на линейна анизотропия на потока и с използуване на закона на Фик). Или: . За плоска граница и насочване на оста Ox по външната нормала последният израз ще има вида . Приемайки линейност на F(x) извън границата на реактора, получаваме, че потокът ще заеме нулева стойност на разстояние от тази граница, където се нарича транспортна дължина. Аналогични разглеждания, но на базата на точното уравнение на неутронния пренос, водят до малко по-различна стойност на дължината на екстраполация d, а именно: d = 0.71l_tr. Следователно, външното гранично условие на свободна повърхност за дифузионното уравнение може да се обобщи като: “F = 0 на екстраполираната външна граница на реактора”, където под екстраполирана граница се разбира реалната граница + дължината на екстраполация d.

Приложимост и подходи за решаване на дифузионното уравнение

За еднородни области с проста геометрия - пластина, цилиндър, сфера, и при допълнителното предположение за "разделимост" на потока, F(r,E)=R(r)y(E), дифузионното уравнение може да се реши аналитично. Предположението за разделимост е добро за еднородни области с достатъчно големи размери, където (с изключение на малкия граничен слой) енергетичният спектър на неутроните y(E) е близък до този в безкрайна среда със същия състав.

Дифузионното приближение се използува за реакторни пресмятания по два принципно различни начина. Първият от тях се съгласува с начина, по който то беше обосновано и получено. Еднородните области са действително съществуващите в активната зона - топлоотделящи елементи, забавител, различни конструкционни елементи. Техните характерни размери са малки и не допускат разделяне на пространствената от енергетичната зависимост на потока. В този случай, подобно на подхода при решаване на уравнението на неутронния пренос, се прилага многогруповото представяне. Енергетичният диапазон на неутроните се разбива на голям брой подинтервали, във всеки от които се предполага, че и се дефинират съответните групови параметри - сечения и коефициент на дифузия. Дифузионното уравнение се разпада на система от G едноскоростни (с независещи явно от енергията решения F_g(r), g=1,...,G) дифузионни уравнения, които се решават при разгледаните по-горе вътрешни и външни гранични условия:

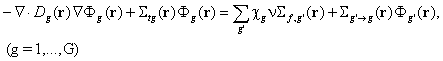
Тъй като пространствената структура на реактора се описва детайлно, а броят на енергетичните групи по необходимост е голям, такъв подход се нарича многогрупов финоклетъчен. Неговата точност и приложимост са ограничени единствено от същността на дифузионното приближение. Този метод не е подходящ за неутронно-физични пресмятания на водно-водните реактори с топлинни неутрони поради малките напречни размери на ТОЕ и малката стъпка на решетката. В топлинната област ТОЕ представляват силно поглъщащи области с малки размери и дифузионното приближение не е коректно. За пресмятане на детайлното пространствено-енергетично разпределение на неутроните в този случай се прилагат по-точни формулировки на уравнението на неутронния пренос.

Тук е уместно да се коментира една принципно важна особеност на решаването на независещото от времето уравнение на неутронния пренос, обща за всички негови специфични формулировки и начини на прилагане. Припомняйки че независимостта от времето означава критичност, т.е. точно равенство между скоростта на възникване и скоростта на изчезване на неутрони от всеки фазов обем, без загуба на общност на направените изводи въпросната особеност ще бъде пояснена на примера на многогруповото дифузионно уравнение. Лесно може да се види, че след въвеждане на подходяща пространствена дискретизация, то ще придобие вида на система от хомогенни линейни алгебрични уравнения, . От хомогенността на системата следва, че:

а) Решението F е определено с точност до множител. Това е израз на физичния факт, че при даден материален състав реакторът може да бъде критичен при различни стойности на неутронния поток.

б) За да има ненулево решение F, е необходимо детерминантата |H| да бъде равна на нула. Това изискване има смисъл на условие за критичност, тъй като |H| зависи от груповите константи (групови коефициенти на дифузия и сечения), а те от своя страна - от концентрациите n на различните нуклиди в реактора. Условието |H| = 0 може да се използува като уравнение за намиране на една избрана концентрация при фиксирани останали - например критичната концентрация на борна киселина или критичното положение на ОР СУЗ. Проблемът, обаче, е че |H| е полином по отношение на търсения критичен параметър и условието за критичност формално ще има множество различни решения. За намиране на единственото физически смислено решение се прилага следният подход. Тъй като при фиксирани групови константи е винаги възможно реакторът да бъде приведен в критично състояние чрез вариране на броя n на неутроните от делене, груповите константи се разделят на общо за цялата линейна система реално положително число l, изпълняващо функцията на критичен параметър, подлежащ на вариране с цел удовлетворяване на условието |H| = 0. Така многогруповото дифузионно уравнение приддобива следната условно критична формулировка:

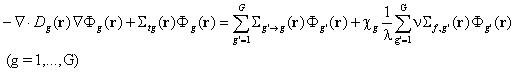
Общият матричен запис на тази система е , което е стандартната задача за търсене на собствените вектори F_i и собствените стойности l_i на матрицата A. По отношение на породените от уравнението на неутронния пренос собствени задачи, за всеки физически допустим набор от материални константи, т.е. макроскопични сечения, могат да се докажат следните математични твърдения:

1. Съществува една единствена реална положителна собствена стойност на задачата, по-голяма от всички останали.

2. Всички елементи на съответствуващия на тази собствена стойност собствен вектор са реални и положителни.

3. Всички останали собствени вектори имат нулеви или отрицателни елементи.

Физически допустим е единствено собственият вектор, съответствуващ на максималната собствена стойност, и то ако последната е равна на единица, тъй като не можем изкуствено да влияем на броя на неутроните, изпускани при делене. В този смисъл, практическата процедура за решаване на уравнението на неутронния пренос за критична размножаваща среда е чрез последователни приближения да се варира материалният състав на средата (напр. концентрацията на борната киселина, положението на ОР СУЗ и т.н.), докато максималната собствена стойност стане единица.

Собствената стойност l, съответствуваща на положително решение за F, е количествена мярка за отдалечеността на състава и размерите на реактора от съответствуващите на критичното състояние. В частност, ако l > 1, реакторът би бил надкритичен и неутронният поток F би нараствал във времето. Обратно, при  < 1 верижната реакция на делене би затихвала с времето и реакторът би бил подкритичен.

Може да се покаже, че l има следната физична интерпретация, отнасяща се както за всеки фазов обем, така и за целия реактор: l = “отношение на пълната скорост на генерация към пълната скорост на загуба на неутрони”. Нужно е да се отбележи, че ако за реална размножаваща среда е различно от единица, решението на условно-критичното уравнение няма да съвпада с действителния неутронен поток F, нито пък действителната стойност на отношението на скоростта на генерация към скоростта на загуба на неутрони ще съвпада със собствената стойност l. Независимо от това, l е полезно физично приближение и наистина представлява количествена мярка за близостта на дадена размножаваща среда до критично състояние. Поради особеното си значение величината l има специално название - ефективен коефициент на размножение k_eff.

Връщайки се сега към темата за приложимостта и подходите за решаване на дифузионното уравнение, ще разгледаме втората принципна възможност за неговото използуване за моделиране на неутронно-физичните процеси в активната зона на ядрените реактори, която се състои в следното. Характерните зони в реактора (горивните касети, поглъщащите наставки на касетите АРК (при ВВЕР-440) и, в някои случаи, отражателят) се представят условно като "хомогенни". За такива големи в сравнение с дължината на разсейване и слабо поглъщащи (поради "смесване" на горивото и забавителя) области дифузионното приближение е вече приложимо. Техните групови константи (сечения, коефициент на дифузия, дължини на екстраполация) се дефинират така, че скоростите на съответните реакции в условно хомогенния случай да бъдат равни на действителните. За сеченията това означава 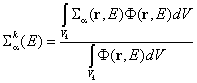, а за коефициентите на дифузия: 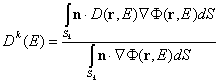. Последното уравнение изразява изискването за запазване на скоростта на утечките през повърхността S_k на условно хомогенизираната пространствена област V_k.

Дифузионното уравнение се интегрира в областта V_k и придобива смисъл на уравнение на неутронния баланс:

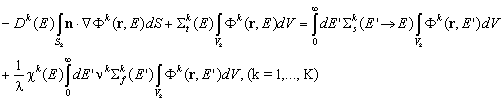
На границите между съседните области V_k се налагат условия за непрекъснатост на потока F(r,E) и тока през границата S_kk’ . На границите с отражателя и вътрешните неразмножаващи области (поглъщащите наставки на касетите АРК) се налагат условия от логаритмичен тип: . Енергетичната зависимост се третира отново чрез дискретизация (групов подход), аналогично на вече разгледаното финоклетъчното многогрупово представяне.

В този случай не може да се очаква пространствената зависимост на решението F^k(r,E) да съвпада с "истинския" поток F(r,E). Надеждата е, че техните интеграли по V_k (или, което е същото, средните им стойности) ще съвпадат. Именно тези средни стойности са физически смислените величини, заради което се решава това дифузионно уравнение, тъй като всъщност предмет на основен интерес е разпределението на енергоотделянето и изгарянето на ядреното гориво в активната зона, които са пропорционални на скоростта на делене.

Проблем при хомогенизацията е невъзможността да се отчетат такива чисто "хетерогенни" ефекти като пространственото и енергетичното самоекраниране на резонансното залавяне, доплеровия (мощностен) ефект и др. Оказва се, че точността на решението (съвпадението на средните стойности) се подобрява при "огрубяване" на енергетичната зависимост на сеченията. Така например, при реакторите от типа PWR (и в частност ВВЕР) целият енергетичен диапазон се разбива на относително малък брой подинтервали. Това е възможно, а и желателно, поради особеностите на формирането на спектъра на плътността на неутронния поток при тези реактори. При тях неутронният спектър над топлинната област (над » 1 eV) се определя основно от отношението на концентрациите на ядрата на водорода към ядрата на ²³⁸U, r_H/r₂₃₈. Тъй като всички касети имат еднаква геометрия и се различават помежду си само по съдържанието на ²³⁵U, което не надхвърля няколко процента, стойността на r_H/r₂₃₈ за всички касети е почти еднаква. Следователно енергетичните спектри на надтоплинните неутрони в различните касети се различават слабо. В топлинната област дължината на дифузия на неутроните е, в зависимост от плътността на водата, 3-4 cm, т.е. няколко пъти по-малка от напречния размер на касетата. Поради това в по-голямата част от обема на касетата неутронният спектър се определя от свойствата на самата касета и слабо зависи от нейното обкръжение. Този ефект се подсилва от факта, че разстоянието между ТОЕ, принадлежащи на две съседни касети, е по-голямо от стъпката на подреждане на ТОЕ в касетата. Така между касетите се образува "буферна зона" от забавител, където топлинният неутронен поток има локален максимум, който допълнително "изолира" касетата от нейните съседи. Едно малогрупово разбиване на неутронния енергетичен спектър се прави така, че във всяка енергетична група формирането на спектъра да се обуславя от един характерен физичен процес и формата на неутронния спектър в рамките на групата да зависи слабо от състава на средата.

Пресмятането на малогруповото пространствено-енергетично разпределение на неутронния поток се прави в реалната геометрия на една горивна касета или за безкрайна решетка от топлоотделящи елементи чрез решаване на уравнението на неутронния пренос в някакъв приложим за случая модифициран вид, но не в дифузионно приближение, което е неприложимо в случая. Това решение (или аналогично на него, отчитащо реалната хетерогенна структура на активната зона) се използува за получаване на коефициентите в дифузионното уравнение за условно хомогенизираните касети, или т. нар. едроклетъчни хомогенизирани дифузионни параметри (коефициенти на дифузия, сечения, дължини на екстраполация).

На етапа на експлоатационните реакторни пресмятания се решава именно последното уравнение, така че да се намери глобалното разпределение на неутронния поток и на скоростите на неутронните реакции (напр. скоростта на делене, респективно енергоотделянето) в реактора в зависимост от конкретната схема на презареждане, предисторията на активната зона (достигнатите вече дълбочини на изгаряне) и конкретния режим на реактора (описан от т.нар. независими параметри на състоянието - входна температура и плътност на топлоносителя, разход на топлоносителя, интегрална топлинна мощност на реактора, концентрация на борна киселина, положение на ОР на СУЗ и т.н.). Дифузионното уравнение за условно хомогенизираните касети се решава най-често при двугрупово представяне на енергетичната зависимост на неутронния поток (топлинна и надтоплинна група).

В обобщение на казаното дотук, структурата на експлоатационните неутронно-физични пресмятания на активната зона на реакторите ВВЕР е следната:

1. В резултат на ядрено-физични експерименти и теоретични анализи се натрупва и систематизира информационна база (библиотека) от ядрени данни (зависещи от енергията микроскопични сечения) за всички нуклиди (и/или вещества), влизащи в състава на реактора.

2. Данните от тази библиотека и информацията за характерния неутронен спектър в реактора се използуват за пресмятане на нужните макроскопични сечения, описващи реалната детайлна хетерогенна структура на решетката от топлоотделящи елементи (или на горивната касета) в серия от "типични" обкръжения и за редица характерни стойности на независимите параметри на състоянието на активната зона. С така получените материални параметри се решава уравнението на неутронния пренос при представяне на енергетичната зависимост в относително малък брой групи (най-често няколко десетки). Получава се серия от решения за неутронния поток F(r,E), съответствуващи на редицата от типове горивни касети (с различни начални обогатявания), техни обкръжения, дълбочини на изгаряне, характерни стойности на независимите параметри на състоянието. Тъй като на този етап се обръща основно внимание на точното моделиране на пространствено-енергетичното разпределение на неутронния поток в решетката от ТОЕ, тези пресмятания често се наричат спектрални. Те се правят само веднъж за даден тип активна зона и са съобразени с изискванията на по-нататъшните едроклетъчни дифузионни пресмятания на неутронно-физичните характеристики на активната зона.

3. Резултатите от спектралните пресмятания се използуват за подготовка на (най-често двугрупови) хомогенизирани дифузионни материални параметри (сечения, коефициенти на дифузия, дължини на екстраполация) като функция на материалния състав на горивните касети (начално обогатяване и дълбочина на изгаряне) и на независимите параметри на състоянието, описващи режима на работа на реактора. Този етап, обикновено наричан апроксимация на хомогенизираните дифузионни материални параметри, се провежда заедно със спектралните пресмятания, но е тясно обвързан с конкретния едроклетъчен дифузионен модел, по който се правят експлоатационните пресмятания на НФХ на АЗ.

4. Получените хомогенизирани дифузионни параметри се използуват за решаване на дифузионното уравнение в двугрупово (понякога и едногрупово) представяне на енергетичното разпределение на неутронния поток за активната зона на реактора, съставена от условно хомогенизирани касети. Именно това са експлоатационните, или оперативни, пресмятания на неутронно-физичните характеристики на активната зона. Те се провеждат с цел избиране на схема на презареждане на активната зона, прогнозиране на продължителността на кампанията и на коефициентите на неравномерност на енергоотделянето по касети, определяне на критичните концентрации на борна киселина, ефектите и коефициентите на реактивността, ефективността на органите на СУЗ и т.н. Такива пресмятания се правят задължително за всяка горивна кампания.

Разделянето на неутронно-физичния анализ на ядрените реактор на такива етапи се обосновава и налага от следните фактори:

а) Обособяването на първия етап (оценяване и систематизиране на ядрените данни) е напълно естествено, тъй като той е предмет на ядрената и неутронната физика и е относително независим от физиката на ядрените реактори.

б) Решаването на уравнението на неутронния пренос за целия реактор при детайлно описване на материалния му състав и геометричната му структура е съпроводено с множество математични и изчислителни трудности, а крайният резултат не би бил особено полезен за целите на експлоатацията на реактора. Наистина, би било известно разпределението на скоростта на всяка неутронна реакция във всеки произволно малък обем от активната зона, но така или иначе върху това разпределение не може пряко да се влияе със средствата за управление на един енергетичен ядрен реактор. За целите на експлоатацията са достатъчни средните стойности на скоростите на някои неутронни реакции (на практика само изгарянето и възпроизводството на ядреното гориво, натрупването на продуктите от делене, поглъщането на топлинни неутрони от течния поглътител и ОР на СУЗ) в достатъчно големи пространствени обеми (призматични слоеве от касетите, съответствуващи на аксиално разбиване на активната зона на до няколко десетки слоя)

в) Експлоатацията на ядрените реактори се подчинява на твърди регламенти, при което схемите на презареждане и работните режими варират в тесни граници и следват характерни за дадения модел реактор закони. Това дава възможност да се разделят по време и място трудоемките и изискващи сериозни изследователски усилия етапи 2 и 3 от сравнително леките и бързи експлоатационни пресмятания на НФХ на АЗ в едроклетъчно двугрупово дифузионно приближение. Допълнителна полза от това разделяне е, че така последните могат да се изпълняват в реално време съвместно с работата на системата за вътрешно-реакторен контрол. Такъв режим на работа дава на операторите допълнителна информация за разпределението на енергоотделянето по обема на активната зона, за текущия баланс на реактивността и за очакваното в близко бъдеще поведение на реактора (свързано с процесите на отравяне), а, от друга страна, позволява точното моделиране на изгарянето, което е нужно за избиране на най-добрата схема за следващо презареждане. Нужно е обаче да се припомни едно много важно ограничение на приложението на разгледания неутронно-физичен модел на ядрения реактор. Дотук навсякъде се предполагаше, че във всеки момент от време реакторът е критичен - т.е. скоростта на верижната реакция е постоянна във времето. Това ограничение не е съществено за моделиране на преходни процеси с големи характерни времена като ксеноново отравяне и всякакви технологично допустими изменения на мощността. Когато обаче характерните времена на преходните процеси станат сравними с времето на генерация на закъсняващи неутрони (секунди и десетки секунди), е нужен съвсем друг подход за описване на неутронния пренос. Този дял от реакторния анализ се нарича реакторна кинетика. Някои елементи на кинетиката, свързани с моделирането на аварийни режими, измерването на реактивността, физическия пуск на реактора, ще бъдат разгледани в следващите глави.

Пространствено и енергетично разпределение на неутроните в процеса на забавяне. Възрастово приближение

В този раздел ще бъде описан един метод за описание на пространственото и енергетично разпределение на скаларната плътност на потока на забавящите се неутрони, в който се използуват елементи от въведената по-горе дифузионна теория. Въпреки че този исторически най-стар метод води до приблизителни резултати и е приложим за относително тежък забавител, напр. графит, той дава добра качествена представа за неутронно-физичните процеси в активната зона на ядрения реактор.

Да разгледаме неутрон, изпуснат при делене с енергия E₀. Той ще се движи праволинейно с тази енергия известно време преди да претърпи разсейващ удар с ядро от средата. След удара, в резултат на който неговата енергия намалява, неутронът ще се движи с тази постоянна намалена енергия до следващия разсейващ удар. Тъй като сега неговата скорост е по-малка, очакваното време до следващия разсейващ удар ще бъде по-голямо от преди. Този процес на движение с постоянна енергия, прекъсвано от разсейващи (и забавящи) удари продължава до достигането на топлинно равновесие със средата, т.е. до топлинна енергия. Доколкото средната логаритмична загуба на енергия при един удар не зависи от енергията (виж определението в Глава 1) и е толкова по-малка, колкото по-голяма е масата на разсейващото ядро, при достатъчно голяма маса зависимостта на енергията на средностатистическия забавящ се неутрон от времето може достатъчно точно да се приеме за непрекъсната. Освен това, за относително тежки разсейващи ядра действителната загуба на енергия при един удар (която е случайна величина) ще бъде достатъчно близка до средностатистическата, така че “прекъснатото” поведение на голям ансамбъл от неутрони в хода на забавянето може със задоволителна точност да бъде описано в съвкупност чрез единствена непрекъсната зависимост на енергията от времето.

Така въведеното приближение, наречено модел на непрекъснатото забавяне, позволява да се състави диференциално уравнение, описващо забавянето на неутроните в непоглъщаща среда (напр. графит, при който поглъщането действително може да се пренебрегне). За целта ще приемем, че всички неутрони, дифундирали в продължителност на време t след генерирането им от източника, имат една и съща летаргия u и ще използуваме връзката между dt и du за извеждане на пространственото разпределение на плътността на забавянето.

Нека всички неутрони, дифундирали в продължителност на време t, имат скорост v, и нека е средният свободен пробег по отношение на разсейването, т.е. средното разстояние, изминавано от един неутрон между два разсейващи удара. Следователно, броят на разсейващите удари в интервала dt след момента t ще бъде . Тъй като x е средната логаритмична загуба на енергия при един разсейващ удар, намаляването на lnE ще бъде равно на x, умножено по броя удари за време dt: , или: .

Именно това е търсеното диференциално уравнение, основано на модела на непрекъснатото забавяне и свързващо летаргията с времето в среда без поглъщане. Нека сега разгледаме в точката на наблюдение с радиус-вектор r неутроните, дифундирали в продължение на време t. През следващия интервал dt те ще изтичат от елементарния обем около r със скорост , където и са съответно скаларната плътност на потока и неутронната плътност в разглежданата точка. При отсъствие на поглъщане тази скорост ще бъде равна на скоростта на намаляване на неутронната плътност с времето: . Придавайки на смисъл на брой неутрони в 1 cm³, дифундирали в интервала от време [t, t+dt] след напускане на източника, и отчитайки еднозначната връзка между du и dt, за броя неутрони в 1 cm³, имащи летаргия в интервала [u, u+du] се получава: . Следователно, . Комбинирането на тъждеството с вече известния израз за води до: 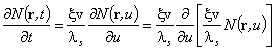. Накрая, с получените връзки и отчитайки определението за l_s: . От получения в Глава 2 асимптотичен спектър на забавящите се неутрони в разсейваща среда с A>1, , и от изведеното пак там твърдение за плътността на забавяне в среда без поглъщане, т.е. (точният извод беше направен за водород, но е в сила и за асимптотичния случай при по-тежка разсейваща среда), следва, че: . След въвеждане на нова променлива, наречена възраст на неутроните t(u), и дефинирана като (или ), се стига до възрастовото уравнение , съвпадащо по форма с уравнението на топлопроводност. Въпреки, че дефинираната по-горе символична възраст t има размерност на площ, може да се покаже, че тя е еднозначно свързана с хронологичната възраст на неутрона t, която от своя страна може да се определи като средното време, необходимо за забавяне на неутрона от първоначалната му енергия E₀ до енергия E.

Решенията за възрастовото уравнение за някои прости геометрии са както следва:

а) Безкраен плосък източник на моноенергетични бързи неутрони в безкрайна среда. Нека от всеки квадратен сантиметър на източника се изпускат S неутрона в секунда с енергия E₀, и нека изберем координатната система така, че източникът да бъде разположен в равнината (y, z). Тогава 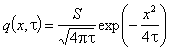. Ако източникът е разположен в равнината x₀, то .

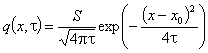б) Точков източник на моноенергетични бързи неутрони в безкрайна среда. Ако източникът изпуска S неутрона в секунда, а позицията му съвпада с началото на координатната система, то . Ако източникът е разположен в точка r₀, .

Вижда се, че при произволна фиксирана възраст пространственото разпределение на плътността на забавяне е гаусова крива. Нейната ширина нараства с възрастта, т.е. с намаляването на енергията, което е физически обяснимо, защото в процеса на забавянето неутроните дифундират все по-далече от източника.

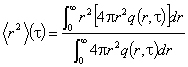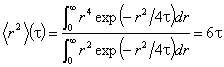Нека сега пресметнем средния квадрат на разстоянието по права линия от точков източник, което неутроните изминават до достигане на дадена възраст t: , където е броят неутрони в сферичния слой между r и r+dr, които в процеса на забавяне достигат възраст не по-малка от t. Замествайки с решението на възрастовото уравнение за точков източник, получаваме: . Следователно, възрастта t е 1/6 от средния квадрат на разстоянието по права линия, което изминава неутронът от момента на неговото изпускане от източника (съответствуващ на нулева възраст) до момента, в който се забавя под енергия, съответствуваща на въпросната възраст.

Тъй като при по-нататъшните разглеждания ще се интересуваме главно от възрастта на топлинните неутрони t_th, е уместно да въведем и често използуваната величина дължина на забавянето на топлинните неутрони, равна на .

Получените в тази глава основни резултати (дифузионно уравнение и възрастово уравнение) ще бъдат използувани по-нататък за приблизително описване на пространствено-енергетичното разпределение на неутронния поток в опростени модели на активната зона на реактора чрез т.нар. дифузионно-възрастово приближение.