4. Верижна реакция на делене. Баланс на неутроните за един неутронен цикъл. Условия за самоподдържане на верижната реакция, коефициент на размножение, реактивност, особености при хетерогенни среди.

Формалното определение на термина верижна реакция на делене, който вече имахме случая да използуваме в предходните глави, е: “процес, при който част от освободените при делене на ядрата неутрони предизвикват делене на други ядра, част от освободените при което неутрони на свой ред предизвикват делене на нови ядра, и т.н.”.

От гледна точка на верижната реакция, могат да бъдат обособени следните характерни етапи от съдбата на един средностатистически неутрон:

- възможност да предизвика делене на присъствуващите в горивото делими нуклиди (напр. ²³⁸U) преди да се забави под прага на сечението за тяхното делене;

- възможност да бъде погълнат в процеса на забавянето (главно в резонансната енергетична област) или да напусне активната зона на реактора;

- след забавянето си до топлинни енергии - възможност да бъде погълнат извън горивната област (в забавителя, конструкционните материали, съсредоточените или разтворени в забавителя поглътители) или да напусне активната зона в процеса на дифузия;

- възможност да бъде заловен от нуклидите в горивото, без да предизвика делене;

- и най-накрая, възможност да предизвика делене след залавянето си от ядро на някой от делящите се нуклиди в горивото (напр. ²³⁵U или ²³⁹Pu).

Във всички случаи, обаче, ако условно си представим, че в даден момент в реакторната среда едновременно възникнат N₀ неутрона от делене, то след известен кратък средностатистически период от време в резултат на верижната реакция на тяхно място ще се появят N₁ = kN₀ неутрона, след повторен такъв период - N₂ = kN₁ = k²N₀ неутрона, и т.н.

Явно е, че при k = 1 верижната реакция ще бъде стационарна и самоподдържаща се. Прието е това състояние да се нарича критичност, а средата в която то се наблюдава - критична. При k > 1 средата е надкритична и с течение на времето броят на неутроните ще нараства неограничено (а с него и скоростите на неутронните реакции). При k < 1 средата ще бъде подкритична и в нея броят на неутроните постепенно ще клони към нула (както, естествено, и скоростите на неутронните реакции).

Множителят k се нарича коефициент на размножение. В Глава 3 той беше най-наред формално въведен като собствена стойност на хомогенното уравнение на неутронния пренос (в частния случай на неговото дифузионно приближение), след което беше показано, че има физичен смисъл на отношението на скоростта на възникване на неутрони към скоростта на тяхното изчезване (както във всеки фазов обем, така и в целия реактор).

В пряка връзка с коефициента на размножение се дефинира величината реактивност r: , чийто физичен смисъл съответно е “относителна разлика между скоростта на възникване на неутрони и скоростта на тяхното изчезване”. От определението за реактивност следва, че r = 0 при критичен реактор, r > 0 - при надкритичен и r < 0 при подкритичен.

Въпреки че начинът на определяне на коефициента на размножение в предходната глава представляваше и практическо указание за начина на неговото пресмятане, по-долу ще бъдат разгледан и един метод за количественото му оценяване, който не предполага по необходимост решаване на уравнението на неутронния пренос или на някоя негова приблизителна формулировка. Този метод има главно историческа стойност, но неговото познаване е полезно за изграждане на представа за неутронно-физичните процеси в ядрените реактори. В началния период на създаване на реакторната теория той е бил едва ли не единствено възможният, тъй като е имал двойното предимство да бъде математически прост и да изисква като входни данни съотношенията между определени скорости на реакции, усреднени по големи енергетични интервали, които могат да бъдат определени твърде точно в резултат на преки експерименти. Така е била заобиколена нуждата от детайлно познаване на стойностите на ядрените сечения.

Най-напред ще разгледаме т.нар. формула на четирите множителя за пресмятане на коефициента на размножение в безкрайна среда k_¥. Под безкрайна среда можем да разбираме безкрайна еднородна среда, но като правило ще имаме предвид безкрайна нееднородна среда, съставена от т.нар. елементарни реакторни клетки. Отчитайки конструкцията на горивните касети на реакторите ВВЕР, ще определим елементарната реакторна клетка като напречното сечение на един горивен елемент (ТОЕ), ограден с принадлежащата му еквивалентна площ забавител. Тук все пак е уместно да се отбележи, че нашите разглеждания в действителност ще бъдат съвсем условни, защото ако формулата на четирите множителя може да даде относително точни резултати за реактори на топлинни неутрони със забавител тежка вода или графит, тя е неподходяща за реакторите с бързи неутрони и трябва да бъде съществено усложнена и видоизменена за прилагане при водно-водните реактори със слабо обогатен уран.

Връщайки се към условно-критичното дифузионно уравнение и разглеждайки частния случай на безкрайна еднородна среда, получаваме:

.

Или, след интегриране по енергия:

.

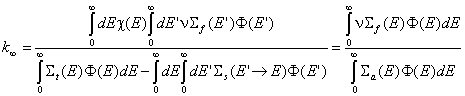Последният израз се дължи на факта, че:

.

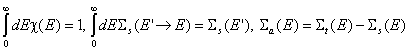Ако би било възможно някак да създадем потока F(E) и да измерим скоростите на генерация и на поглъщане на неутрони, би могло да получим k_¥ като тяхно отношение. Оказва се, че няма прост и пряк начин за измерване на тези две скорости на реакции. Възможно е обаче да се разложи това отношение на четири множителя, всеки от които е също отношение на скорости на реакции, но може да бъде измерен експериментално със задоволителна точност.

По-нататък ще разгледаме единствено случая на безкрайна периодична решетка от елементарни реакторни клетки, тъй като хомогенният случай се обобщава пряко на базата на резултатите за нехомогенния. Пространственото разпределение на потока (r,E) ще бъде периодично и еднакво за всички елементарни клетки, така че изразът за k_¥ се обобщава по следния начин: 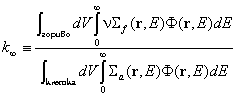. Този израз може да се запише като произведение на четири отношения:

,

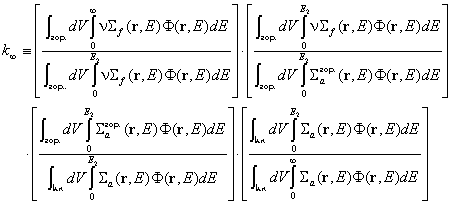където E₂ е граничната енергия (» 1 eV) между топлинните енергии (при които придобиването на енергия в резултат на разсейване е съществено) и енергетичния диапазон на забавящите се неутрони (в който неутроните могат единствено да губят енергия при разсейване).

Названието и типичният начин за измерване на всеки от тези четири множителя са както следва.

Коефициент на размножение с бързи неутрони e

Първият множител се нарича коефициент на размножение с бързи неутрони e и се определя по следния начин: 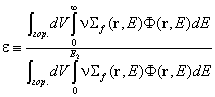. Това е отношението на пълната скорост на генерация на неутрони от делене в решетката към скоростта на генерация на неутрони поради делене с топлинни неутрони. От определението следва, че зависи пряко само от на различните делящи се нуклиди (означавани с индекса j) в горивния елемент. зависи непряко и не много съществено от материалния състав на цялата елементарна клетка, тъй като от него се определя F(r,E). Ако се допусне, че n^j е постоянно и е еднакво за всички делящи се нуклиди, то e ще бъде отношение на скоростите на делене. Те от своя страна могат да бъдат определени по активацията на тънко фолио от материала на горивото при енергетично разпределение на потока F(E), типично за изследваната решетка. Активността на фолиото след облъчване с такъв неутронен поток ще бъде пропорционална на натрупаните продукти на делене. Експериментът се прави при равни други условия веднъж с фолио без обвивка, при което активността B на фолиото е представителна за 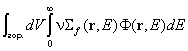, и веднъж със същото фолио, но обвито с кадмий. Кадмият има резонанс на сечението за поглъщане на неутрони, в който то нараства от около 0 b до » 7500 b при E = 0.5 eV и остава такова в цялата топлинна област. Следователно активността C на покритото с Cd фолио ще бъде функция на 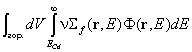. Тогава: e » B/(B-C).

В реактор от типа ВВЕР основната част от деленията протича в топлинната област, така че коефициентът на размножение с бързи неутрони e е едва около 1.04 и се дължи практически единствено на деленето на ²³⁸U (сеченията за делене с бързи неутрони за ²³⁵U и ²³⁸U са практически еднакви, а концентрацията на ²³⁵U е едва 3-4 %). По принцип e нараства с намаляването на концентрацията на забавителя в елементарната клетка (на плътността на забавителя, на стъпката на решетката от горивни елементи и т.н.), тъй като тогава нараства дялът на бързите неутрони в енергетичното разпределение F(E).

Коефициент на размножение на топлинните неутрони h

Вторият множител се обозначава с h и се нарича просто "ета на горивото". Това е отношението на скоростта на генерация на неутрони поради делене с топлинни неутрони към скоростта на поглъщане на топлинни неутрони в горивото: 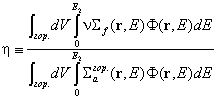. включва поглъщането на неутрони от ²³⁵U, ²³⁸U, продуктите от деленето и образувалите се изотопи на Pu. Следователно, h за работещ енергетичен реактор ще се изменя в хода на кампанията. За реактори от типа ВВЕР h » 1.8. При малки дълбочини на изгаряне h може леко да нарасне поради натрупването на плутоний ( е много по-голямо от в топлинната област). По-нататък h намалява поради натрупването на поглъщащи неутроните продукти на делене (шлакуване и отравяне). Сеченията за поглъщане и делене на горивото имат приблизително еднаква енергетична зависимост в топлинната област и, следователно, h зависи основно от нуклидния състав на горивото и слабо от енергетичното разпределение на неутронния поток.

Класически начин за експериментално определяне на h е следният. Малък образец от горивото се поставя в центъра на права празна тръба, поставена в резервоар с вода, в която е разтворена манганова сол. По тръбата се пуска сноп топлинни неутрони (от изследователски реактор) и се измерва отслабването на неутронния поток поради поглъщане в горивния образец. По този начин се оценява 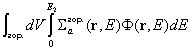. Изпуснатите от образеца неутрони от делене се поглъщат от мангановия разтвор ((0.025 eV) = 13 b, (0.025 eV) = 0.664 b) и активират мангана, чиято активност е мярка за 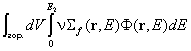. Движещият се по тръбата неутронен сноп няма принос в активацията поради насоченото движение на неутроните по оста на тръбата.

Коефициент на използуване на топлинните неутрони f

Третият от четирите множителя се нарича коефициент на използуване на топлинните неутрони f: 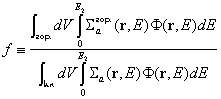. Това е отношението на скоростта на поглъщане на топлинни неутрони в горивото към пълната скорост на поглъщане на топлинни неутрони в елементарната реакторна клетка. При определянето на f е много по-важно да се отчита пространственото разпределение на потока, отколкото при определянето на e или h. Поради това измерването на f трябва да се прави в действителната геометрия на елементарната клетка. Енергетичната зависимост на потока на топлинните неутрони F(r,E) не влияе съществено на f, тъй като енергетичната зависимост на всички участвуващи в израза сечения е приблизително еднаква: µ 1/v. Следователно стойността на f зависи основно от относителните стойности на микроскопичните сечения при някаква фиксирана енергия (напр. 0.025 eV) и от формата (пространственото разпределение) на топлинния поток в клетката.

Измерванията на f се основават на определяне на тази форма. На различни места в клетката се поставят тънки фолиа от активиращ се в потока от топлинни неутрони материал и по тяхната относителна активност се съди за F(r,DE), където DE е енергетичният интервал, в който настъпва активация. Резултатът се използува за пресмятане на f по формулата: .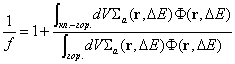

Стойностите на f за водно-водните реактори са от порядъка на 0.8. Стремежът за увеличаване на стойността на f означава намаляване на вредното поглъщане на неутрони в забавителя и обвивката на горивото и изравняване на пространственото разпределение на потока на топлинните неутрони в клетката (той неизбежно е по-малък в горивната област, тъй като забавянето на неутроните става извън горивото, а поглъщането им - в горивната област). Материалният състав на клетката обаче обикновено се избира по други съображения, а промените в геометрията на решетката, увеличаващи f, обикновено водят до намаляване на някой от другите множители. Поради това търсенето на максимална стойност на k_¥ за решетката е предмет на компромис между множество фактори.

Зависимостта на коефициента на размножение на реакторите с борно регулиране от концентрацията на борна киселина в забавителя е основно за сметка на намаляване на f поради увеличеното поглъщане на топлинни неутрони извън горивото. Обратно - намаляването на плътността на забавителя при повишаване на температурата му води до повишаване на f, тъй като намалява едновременно както поради намаляването на ядрената концентрация n^заб., така и поради зависимостта на от енергията на топлинните неутрони по закона "1/v".

Вероятност за избягване на резонансното поглъщане p

Последният множител се нарича вероятност за избягване на резонансното поглъщане p и се определя по следния начин:

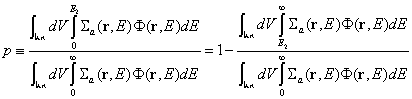
Това е отношение на скоростта на поглъщане на топлинни неутрони навсякъде в клетката към скоростта на поглъщане на неутрони с всякакви енергии навсякъде в клетката. Следователно то изразява вероятността неутроните да избягнат залавяне при енергии над топлинната. Тъй като в решетки с природен или слабо обогатен уран залавянето над топлинната област става предимно в резонансния участък на областта на забавяне, то p има смисъл на "вероятност за избягване на резонансно залавяне". За хомогенна размножаваща среда с природен уран са типични много ниски стойности на p - около 0.7, което, даже и при оптимизация на материалния състав, прави невъзможно създаването на хомогенен реактор с природен уран. Начинът за повишаване на p е пространственото разделяне на горивото от забавителя. Така са устроени всички топлинни реактори с природен или слабообогатен уран. В такава хетерогенна среда ако даден неутрон в процеса на забавянето си достигне енергията на някой от резонансите на сечението за поглъщане в ²³⁸U, той с голяма вероятност ще се разсее в друго ядро на забавителя преди да навлезе в горивния елемент. Ако това стане, неутронът ще е загубил от енергията си и ще избегне залавяне в резонанса. Така от резонансно залавяне са застрашени само неутроните, които достигат резонансни енергии в непосредствена близост до горивния елемент. Този повишаващ стойността на p ефект се нарича пространствено самоекраниране. При нарастване на температурата на средата ширините на резонансите на сеченията, измерени в енергия на неутрона в системата на центъра на масите на неутрона и ядрото-мишена, се увеличават, но площта под кривата на резонанса остава непроменена. Това явление се нарича доплерово разширение на резонанса. Прието е ширината на резонанса DE да се означава с G и да се измерва като ширина на кривата s_a(E) на половината й височина. Ширината G е много малка. Така например, най-важният резонанс на s_a на ²³⁸U има следните параметри: E₀ = 6.67 eV, G = 0.026 eV и s_a(E₀) = 2.16´10⁵ b. Тъй като спектърът на забавящите се неутрони F(E) е пропорционален на 1/E, изменението на потока в границите на този резонанс ще бъде , така че в рамките на резонанса спектърът може да се приеме за плосък: F₀ µ 1/E₀. Следователно, скоростта на резонансно поглъщане (n е ядрената концентрация на резонансния поглътител) би трябвало да остане постоянна, независимо от доплеровото разширение. Практически такава ситуация обаче може да настъпи само ако резонансният поглътител е с относително ниска концентрация - напр. ²³⁸U в хомогенна смес със забавител и резонансното поглъщане не деформира спектъра на забавящите се неутрони.

Удобна мярка за представяне на s(E) за целите на реакторния анализ е скоростта на резонансно поглъщане в рамките на един резонанс при спектър на забавящите се неутрони 1/E, наречена резонансен интеграл I: . С помощта на тази величина вероятността за избягване на резонансно поглъщане p може да се пресметне по следния начин: Вероятността за поглъщане в i-тия резонанс е числено равна на скоростта на поглъщане в резонанса (т.е. на броя неутрони, погълнати в резонанса за единица време в единица обем), делена на броя неутрони , достигащи в процеса на забавяне енергията на резонанса. Според модела на "непрекъснато забавяне" (голям брой разсейвания, всяко съпроводено с малка загуба на енергия), , където x е средната логаритмична загуба на енергия при един акт на разсейване, a е източникът на неутрони от делене, намален с вероятностите за избягване на резонансите с енергии, по-високи от тази на разглеждания резонанс E_i: . Следователно, за i-тия резонанс: 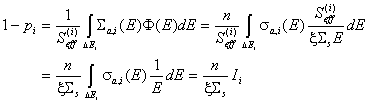. Доколкото вероятността за поглъщане в i-тия резонанс е малка и , то: 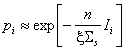. (Това представяне е целесъобразно при натрупване на произведения от вероятности.) Така, за всички резонанси се получава: 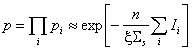. (Тук е уместно да се отбележи, че този израз се основава на редица приближения и може да се използува за реални пресмятания след множество допълнителни корекции.)

В горивния елемент на хетерогенния реактор концентрацията на ²³⁸U е изключително висока и резонансното поглъщане деформира неутронния спектър, така че F(E) придобива минимум в енергетичния интервал на резонанса DE (т.е. настъпва дефицит на неутрони с енергии в областта на резонанса). Ако в такава среда се повиши температурата, резонансът на s_a(E) ще се разшири, но ще стане по-плитък. По-ниските стойности на s_a(E) около максимума на резонанса ще доведат до по-слабо деформиране на неутронния спектър и съответно по-високи стойности на F(E). Заедно с разширяването на интервала DE, в който настъпва поглъщането, сумарният резултат е увеличаване на скоростта на резонансно поглъщане . Този ефект, водещ до намаляване на вероятността за избягване на резонансно поглъщане p при увеличаване на температурата на концентриран резонансен поглътител, се нарича енергетично самоекраниране.

В хетерогенния реактор по-голямата част от енергията на делене се отделя незабавно в горивните елементи. По тази причина нарастването на мощността (скоростта на делене) увеличава незабавно температурата на горивото още преди топлината да се отдаде на забавителя. Този процес води до незабавно спадане на коефициента на размножение поради намаляването на p практически без да се засягат останалите три множителя. Така се създава естествена отрицателна обратна връзка по мощност, която е основен фактор за управляемостта и ядрената безопасност на реакторите ВВЕР. Прието е, макар и неточно, това явление да се нарича доплеров ефект.

Обобщавайки казаното по-горе, хетерогенната структура на реактора се отразява на вероятността за избягване на резонансно поглъщане p по два независими начина:

- нарастване на p в сравнение с хомогенния случай, дължащо се на пространственото самоекраниране;

- намаляване на p с увеличаване на температурата на горивото (мощността на реактора), дължащо се на енергетичното самоекраниране при доплеровото разширяване на резонансите.

При конструиране на решетката основен стремеж е повишаването на k. По отношение на p това би означавало "по-голяма хетерогенност" - т.е. по-големи горивни елементи, оградени с по-големи области забавител. Така обаче би се понижила стойността на коефициента на използуване на топлинните неутрони f, докато стойностите на и биха останали почти непроменени. Постигането на максимален k_¥ е въпрос на компромис между f и p. При оптимизирана решетка с природен уран и f и p са по около 0.9. Решетката на реакторите ВВЕР не е оптимизирана по k_¥, а по топлотехнически, якостни и други параметри. Типична стойност на p за ВВЕР е 0.75-0.8.

Точното пресмятане на p за хетерогенна решетка е възможно, но е трудно от математическа и изчислителна гледна точка. Съществуват множество прости алгебрични изрази, които са основани на неубедителни теоретични аргументи, но са проверени и емпирично коригирани чрез сравнение с измервания и по-прецизни теоретични разглеждания. Те свързват p с размера на топлоотделящия елемент и отношението между обемите на забавителя и горивото в елементарната реакторна клетка.

Измерванията на p се правят в условия на реалната решетка и са твърде косвени. Един от методите се основава на измерване на активността на ²³⁹Np в непокрити и покрити с кадмий фолиа от ²³⁸U с диаметъра на горивния елемент и представляващи неделима част от него. (реакцията е ). Измерването на равновесната концентрация на ²³⁹Np по g-активността дава възможност за определяне на следното отношение: 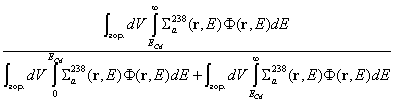. Тогава, ако може да се измери или пресметне отношението 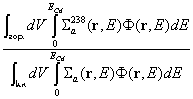и ако се пренебрегне 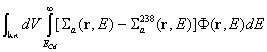, като при това за гранична енергия E₂ се приеме E_Cd, може да се оцени стойността на p.

От приведените определения за множителите e, p, f и h се вижда, че те могат да бъдат директно обобщени за случая на хомогенна реакторна среда. Доколкото, обаче, реалните реактори са почти без изключение хетерогенни, а представянето им като хомогенни или съставени от хомогенни области е опростяваща абстракция, най-често множителите се оценяват за реалната хетерогенна реакторна структура, а получените резултати се пренасят за условно хомогенизираната реакторна среда.

За крайна среда, какъвто, разбира се, е случаят с реалните реактори, формулата на четирите множителя се разширява по следния начин: , където P_f е вероятността за избягване на утечка на бързите неутрони в процеса на забавяне, а P_th е вероятността за избягване на утечка на топлинните неутрони в процеса на дифузия. Прието е този израз да се нарича формула на шестте множителя, а коефициентът на размножение в реална крайна реакторна среда да се нарича ефективен коефициент на размножение и да се бележи с k_eff. Изрази за вероятностите P_f и P_th ще бъдат получени в следващата глава.

Най-накрая е уместно отново да се напомни обстоятелството, че коефициентът на размножение е глобална характеристика на реактора и в този смисъл да се говори за коефициенти на размножение (или реактивност) на части от активната зона, напр. отделни горивни касети, е формално неправилно. В такива случаи в действителност се имат предвид само стойности на k_¥, които следва да се разглеждат материални характеристики на средата. В частност, в критичния реактор коефициентът на размножение е равен на единица във всеки произволен геометричен обем, т.е. има абсолютно точно равенство между скоростта на възникване на неутрони в този обем и на скоростта на изчезване на неутрони от него, което се установява за сметка на преноса на неутрони от или към въпросния обем.