5. Условия за критичност на хомогенни и хетерогенни среди в дифузионно приближение. Критично уравнение, материален и геометричен параметър. Разпределение на неутронния поток в активната зона, влияние на отражателя

Главен предмет на разглежданията в настоящата глава ще бъдат условията, при които реакторът е в критично състояние (т.е. в него може да протича самоподдържаща се верижна реакция на делене). Най-напред, обаче, е уместно да се направят следните забележки, първата от които е съвсем очевидна:

- при липса на външен източник на неутрони верижната реакция на делене не може да започне, независимо от размножаващите свойства на средата;

- при наличие на външен източник стационарни състояния са възможни и в подкритична среда, доколкото неутроните от източника компенсират загубата на неутрони от поглъщане и утечка;

На началния етап анализът ще бъде ограничен за случая на верижни реакции с топлинни неутрони. Физически това означава, че отношението на броя на атомите на забавителя към броя на атомите на делящия се нуклид е толкова голямо, че само относително малка част от неутроните се залавят в процеса на забавяне. Ще се предполага също така, че плътността на забавянето, а следователно и източниците на топлинни неутрони в средата, ще се описват от възрастовото уравнение. За простота на разглеждането, но без загуба на общност, ще се предполага, че неутроните от делене и неутроните от външния източник имат еднаква начална енергия. Изведеното в Глава 3 дифузионно уравнение ще се използува единствено за моделиране на преноса на топлинните неутрони, които от своя страна ще се разглеждат като моноенергетични. Връщайки се към обосноваването на закона на Фик в Глава 3 следва да се отбележи, че P₁ уравненията при липса на енергетична зависимост ще придобият опростения вид: 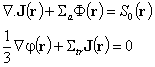, където , а допускането за “слабо поглъщане”, т.е. отпада автоматично.

Съгласно направените уговорки, нестационарното уравнение на дифузия на топлинните неутрони може да се запише по следния начин:

, където чрез независимостта на дифузионния коефициент и сеченията от координатите е предположена хомогенна среда, а е източникът на топлинни неутрони. Този източник е равен на броя на неутроните от делене и от външния източник в единица обем, достигащи за единица време топлинна енергия. При липса на поглъщане в процеса на забавяне този брой би бил равен на решението на възрастовото уравнение при възраст на топлинните неутрони . Наличието на слабо поглъщане в процеса на забавяне може приблизително да се отчете чрез умножаване на по вероятността за избягване на резонансно залавяне p, т.е. .

Така, за опростено двугрупово описване на пространственото и енергетичното разпределение на неутроните в крайна еднородна среда трябва да се реши системата от диференциални уравнения 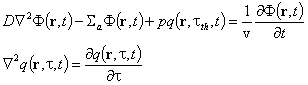, удовлетворяваща подходящи начални и гранични условия.

Преди да пристъпим към тяхното определяне е нужно да направим още една уговорка. Както следва от изложеното в Глава 3, плътността на забавяне има своя специфична зависимост от времето. Тъй като, обаче, времето за забавяне обикновено е много по-малко от времето на дифузия на топлинните неутрони, може да се приеме, че изменението на във времето при всички стойности на t ще се определя само от изменението на потока на топлинните неутрони. Впрочем, записът на първото уравнение от системата съответствува именно на това допускане.

Едно от търсените условия се получава при разглеждане на плътността на забавяне на неутроните с енергия, равна на енергията на източника, . От определенията в предходната глава лесно може да се види, че при поглъщането на един топлинен неутрон възникват fhe бързи неутрона от делене. Тъй като коефициентът на размножение в безкрайна среда k_¥ е равен на fhep, то отношението k_¥/p ще бъде числено равно на броя на забавилите се до топлинна енергия бързи неутрони от делене, възникнали при поглъщане на един топлинен неутрон в реакторната среда. Следователно:

, където е външният неутронен източник.

Полученият израз представлява условието за връзка между дифузионното уравнение за топлинните неутрони и възрастовото уравнение. Той, заедно с въведената по-горе система, образува т.нар. дифузионно-възрастово приближение на уравнението на неутронния пренос. Следва да се отбележи, че поради своите множество ограничения това приближение не може да се използува за реален неутронно-физичен анализ на процесите в активната зона на леководните реактори, но макар и неговата стойност да е главно историческа, разглеждането му в тази глава ще даде добра качествена физична представа за тези процеси.

Граничните условия за системата се получават чрез разглеждане на потока и на плътността на забавяне на границата на реактора. Ако размножаващата среда не е оградена с отражател и за простота приемем, че дължината на екстраполация (виж Глава 3) не зависи от енергията, тези условия ще имат вида: F = 0 и q = 0 на екстраполираната външна граница.

Началните условия за F и q са стандартни:.

За решаване на възрастовото уравнение най-често се прибягва до разделяне на променливите, , при което то придобива вида: . Тъй като лявата част зависи само от r, а дясната - само от t, всяка от тях може да бъде приравнена на константа: , или , и . Решението на последното уравнение е , където A е подлежаща на определяне константа. B² трябва да бъде реална положителна величина, защото плътността на забавянето не може да нараства с увеличаване на възрастта t.

Доближаване до критично състояние

Да разгледаме размножаваща среда във формата на безкраен плоско-паралелен слой с крайна дебелина a (включваща дължината на екстраполация). Нека външният неутронен източник е равномерно разпределен в равнината на симетрия на слоя. Ако началото на координатната система се избере в равнината на източника и оста Ox е насочена перпендикулярно на тази равнина, то пространственото разпределение на плътността на забавяне (и на потока) ще зависи от единствената променлива x и уравнението за R(r) може да се запише като: .

Лесно може да се покаже, че решенията на това уравнение, удовлетворяващи изискванията за симетрия и граничното условие за плътността на забавяне (q = 0 при x = a/2), ще имат вида: , където n е произволно цяло нечетно число. Тоест, величината B² ще приема стойности , които представляват собствени стойности на задачата, всяка от които съответствува на собствена функция X_n. Най-малката собствена стойност съответствува на n = 1.

Общото решение на възрастовото уравнение ще бъде сума на частните решения по всички нечетни стойности на n: . Външният източник, разположен в равнината на симетрия на слоя, може да се представи чрез ред на Фурие: , където n отново е цяло нечетно число. От условието за връзка между дифузионното и възрастовото уравнение следва, че: . Замествайки изразите за плътността на забавяне и за потока на топлинните неутрони в дифузионното уравнение за топлинните неутрони, и отчитайки, че събираемите, отговарящи на различни стойности на n са линейно независими, се получава: .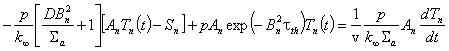

Или: 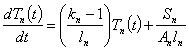, където и , а и са съответно дължината на дифузия и времето на живот на топлинните неутрони.

Решението на това уравнение е: 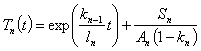, а потокът на топлинните неутрони съответно ще бъде:

.

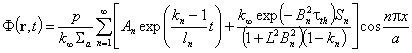Вторият член в квадратните скоби описва влиянието на външния източник върху потока на топлинните неутрони, а първият член отчита единствено приноса на размножаващата среда.

Полученият израз позволява да се формулира условието, при което размножаващата среда ще премине в критично състояние. С увеличаване на дебелината a намаляват стойностите на и съответно нарастват величините k_n. Докато размерите на реактора са такива, че k_n < 1 за всички цели нечетни n, първият член в квадратните скоби ще намалява експоненциално и след известно време ще изчезне, така че единственият начин за поддържане на стационарно състояние ще бъде присъствието на външен източник. С увеличаване на размера на реактора ще настъпи момент, когато най-малкото от числата , а именно , ще стане такова, че k₁ = 1. Тъй като очевидно , първият член в квадратните скоби ще клони към константа, а вторият ще приеме безкрайна стойност. Следователно, за достигане на стационарно състояние (при което верижната реакция на делене ще бъде самоподдържаща се) трябва да бъдат премахнати всички независими неутронни източници.

Условието се нарича критично уравнение. Интерпретирано като условие за размерите на реактора, то означава, че реакторът ще бъде критичен, ако размерите му са такива, че съответствуващата им най-малката собствена стойност B₁ удовлетворява критичното уравнение.

Връщайки се към решението на дифузионно-възрастовото уравнение при разглежданата геометрия, за критичната дебелина a (и без външен източник) то ще бъде, . Константата A по принцип не подлежи на определяне, защото без външен източник уравнението е хомогенно. Физически това означава, че реакторът може да бъде критичен при всякакво ниво на неутронния поток. За плътността на забавяне на топлинните неутрони се получава: (индексът на B₁ тук и по-долу ще бъде пропускан). Следователно, тази плътност ще бъде навсякъде пропорционална на потока на топлинните неутрони, защото при фиксирана енергия величините k_¥, p, S_a и са константи.

Въпреки че приведените дотук основни резултати се отнасят за разглежданата конкретна геометрия, те не зависят от действителната форма на реактора и са приложими за всяка критична система, в която източникът на топлинни неутрони се описва чрез възрастовото уравнение.

Материален и геометричен параметър

Поради пропорционалността между потока на топлинните неутрони и плътността на забавянето в критичния реактор, потокът на топлинните неутрони също ще удовлетворява вълновото уравнение: , където параметърът е най-малката собствена стойност на това уравнение при гранично условие за нулев поток на екстраполираната граница. От друга страна, ако е приложим моделът на непрекъснатото забавяне (т.е. възрастовото уравнение), критичното уравнение за хомогенен реактор без отражател ще бъде: .

От гледна точка на определянето на условията за критичност следва да се разграничат следните два смисъла на параметъра B²:

Материалният параметър е тази стойност на , която удовлетворява критичното уравнение. Поради това в критичния реактор пространственото разпределение на потока ще се определя от уравнението . От критичното уравнение се вижда, че материалният параметър е свойство на размножаващата среда, тъй като зависи само от материалните константи k_¥, t_th и L².

Геометричният параметър , от своя страна, е минималната собствена стойност на вълновото уравнение при гранично условие за нулев поток на екстраполираната граница. Ясно е, че тази стойност ще зависи само от формата и размерите на реактора.

От приведените определения следва, че условието за критичност може да се запише във вида: . Доколкото, както ще бъде показано по-долу, геометричният параметър намалява с нарастване на размера на реактора, при реакторът ще бъде надкритичен, а при - подкритичен.

На базата на условието за критичност може да се формулира и следното определение за ефективния коефициент на размножение на реактора, изцяло съгласуващо се с приведеното в Глава 3: .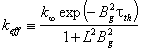

Физичният смисъл на отчитащите крайния размер на реактора множители и може да се проследи чрез следните разсъждения. Както беше посочено по-горе, броят на топлинните неутрони, поглъщани в 1 cm³ за 1 sec, е равен на . По определение, k_¥ е равен на средния брой топлинни неутрони, получавани за един цикъл при поглъщането на един топлинен неутрон в безкрайна среда. Следователно, в безкраен реактор, т.е. при липса на утечка в хода на забавянето, плътността на неутронния източник ще бъде . От друга страна, действителният брой неутрони, достигащи топлинна енергия в 1 cm³ за 1 sec, е . Следователно, множителят е равен на вероятността за избягване на утечка на бързите неутрони в процеса на тяхното забавяне. Скоростта на утечка на топлинните неутрони, т.е. броят топлинни неутрони, напускащи поради дифузия 1 cm³ за 1 sec, е . Тъй като броят на топлинните неутрони, поглъщани в 1 cm³ за 1 sec, е равен на , отношението на утечката на топлинни неутрони към поглъщането на топлинни неутрони във всяка точка, а следователно и в реактора като цяло, е равно на . Или, (“поглъщане на топлинни неутрони”)/( “поглъщане на топлинни неутрони”+”утечка на топлинни неутрони”) = . Следователно, тази величина е относителният дял на забавените в реактора топлинни неутрони, които след забавянето си са погълнати. С други думи, е вероятността един топлинен неутрон да избегне утечка при дифузията си и да остане в реактора.

Разпределение на потока и геометричен параметър за хомогенни реактори без отражател с различни форми

По -долу ще бъдат получени решения на вълновото уравнение и съответните им стойности на геометричния параметър за следните случаи: безкраен слой с крайна дебелина, правоъгълен паралелепипед, сфера, цилиндър с крайна височина.

а) безкраен плосък реактор с крайна дебелина

Нека екстраполираната дебелина на слоя е H = H₀ + 2d, а началото на координатната система е разположено в центъра на слоя. В този случай вълновото уравнение ще съдържа само една независима променлива - x: , а граничното условие е F(x) = 0 при x = ±H/2. Тъй като е реална положителна величина, от изискването за крайна стойност на F(x) във вътрешността на слоя и за нулева стойност на екстраполираната граница следва, че допустимо решение на това уравнение е . От граничното условие следва, че , където n е нечетно число. Доколкото геометричният параметър по определение е най-малката възможна собствена стойност, се получава . Стойността на H, при която геометричният параметър става равен на материалния, т.е. 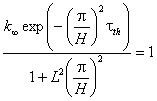, се нарича критична дебелина на безкрайния плосък реактор. Пространственото разпределение на потока в този реактор ще бъде: .

а) реактор с формата на правоъгълен паралелепипед

Нека дължините на ребрата на паралелепипеда, включващи екстраполираните добавки, са a, b и c, а началото на координатната система е в центъра на паралелепипеда. Вълновото уравнение ще бъде: , а граничните условия: при или или . Въвеждайки разделяне на променливите, , вълновото уравнение може да се запише във вида: . Тъй като всяко от първите три събираеми е функция на една променлива, независима от останалите, а сумата им винаги трябва да бъде равна на константа, е възможно полагането: , , , където . Естествени решения на получените три уравнения, удовлетворяващи изискването за симетрия и можещи да заемат нулева стойност на екстраполираната граница, са: , и . Явно е, че за целта a², b² и g² трябва да бъдат реални положителни величини. От граничните условия следва, че техните минимални възможни стойности са , и . Така за геометричния параметър и разпределението на потока се получава: и . Лесно може да се покаже,че при дадена стойност на реакторът ще има минимален обем, когато трите му линейни размера са равни помежду си, т.е. има формата на куб със страна a такава, че . Или: . Този минимален обем ще бъде . Действителната стойност на критичния обем се получава от критичното уравнение, аналогично на предходния случай.

в) Сферичен реактор

Нека екстраполираният радиус на сферата е R, а началото на координатната система е разположено в нейния център. Тогава потокът няма да зависи от сферичните координати q и j, така че вълновото уравнение ще придобие вида: с гранично условие . Общото му решение при положително е . За да бъде то крайно при r ® 0, косинусовият член трябва да бъде отхвърлен, така че: . Граничното условие е . Тъй като A и R са различни от нула, условието може да бъде удовлетворено само при , където n произволно цяло число. Следователно, минималната възможна собствена стойност на уравнението, при която то има ненулево решение, ще съответствува на n = 1: . Геометричният параметър е свързан с обема по следния начин: . Разпределението на потока ще бъде , където критичният радиус R следва да се получи като решение на критичното уравнение.

г) Краен цилиндричен реактор

Нека екстраполираният радиус на цилиндъра е R, екстраполираната му височина - H, а координатната система е с начало в центъра на цилиндъра и ос z насочена по оста на цилиндъра. Тогава решението ще зависи само от координатите r и z, при което вълновото уравнение ще има вида: . Граничните условия са: при или . Решението на това уравнение ще се търси чрез разделяне на променливите: , така че то може да се запише като: . Тъй като първият член зависи само от r, вторият - само от z, а сумата им трябва да бъде константа, то всеки от тях може да се приравни на константа. В този смисъл, нека: и , където . След известни преобразования и въвеждане на нова независима променлива , уравнението за може да се запише като уравнение на Бесел от нулев ред: . При положителна стойност на a² общото решение на това уравнение е: , където J₀ и Y₀ са функциите на Бесел от нулев ред и съответно първи и втори род, а при отрицателна стойност на a² - , където I₀ и K₀ са модифицираните функции на Бесел от нулев ред и съответно първи и втори род. Изборът между двете възможности се прави на базата на граничните условия. Така се оказва, че Y₀, I₀ и K₀ трябва да бъдат отхвърлени, защото Y₀ ® -¥ и K₀ ® +¥ при u ® 0, а I₀ ® +¥ при u ® +¥. Следователно, единственото допустимо решение е , а a² > 0. Стойността на a се определя от граничното условие: . Минималната стойност на a (а съответно и на ), удовлетворяваща това уравнение, е първата нула на J₀, а именно 2.405. Така се получава , т.е. , а за радиалната компонента на решението на вълновото уравнение - . Третирането на аксиалната компонента е аналогично на разгледания вече случай за безкраен слой, с резултати: и . Окончателно, за геометричния параметър се получава: , а за потока в краен цилиндричен реактор: , където R и H са съответно критичният радиус и критичната височина. Може да се покаже, че при фиксиран геометричен параметър минимален обем ще има цилиндърът с размери и . Този минимален обем ще бъде .

По-долу ще бъдат обобщени получените за разгледаните четири случаи резултати.

Геометричен параметър за хомогенни реактори без отражател с различни форми

Форма	Геометричен параметър B	Минимален критичен обем
Безкрайна пластина		-
Правоъгълен паралелепипед
Сфера
Краен цилиндър

Разпределение на потока на топлинните неутрони в критични хомогенни реактори без отражател с различни форми

Форма	Координати	Функция	Променлива u
Безкрайна пластина	x
Правоъгълен паралелепипед	x
	y
	z
Сфера	r
Краен цилиндър	r
	z

Както се вижда от таблицата, във всеки от разгледаните случаи на екстраполираната граница съответствува u = 1, а на центъра на реактора - u = 0. Графиките на функциите на u в интервала от 0 до 1 са показани на долната фигура.

От близостта на трите криви следва, че в първо приближение те могат да се заменят с косинус.

В рамките на това изложение е уместно да се въведе и едно често използувано приближение на критичното уравнение за реактори с големи размери, т.е. с много малка стойност на . В този случай . Така условието за критичност придобива вида: . Или, пренебрегвайки малките от втори порядък, . След въвеждане на величината площ на миграция , за приблизителния израз на условието за критичност окончателно се получава: . Тъй като t_th има смисъл на 1/6 от средния квадрат на разстоянието по права линия, изминавано от неутрона от момента на възникването му при делене до момента на забавянето му до топлинна енергия, а квадратът на дължината на дифузия L² е 1/6 от средния квадрат на разстоянието по права линия, изминавано от топлинния неутрон при неговата дифузия до момента на поглъщането му, площта на миграция M² може да се интерпретира като 1/6 от средния квадрат на разстоянието по права линия, което един неутрон изминава от възникването му като бърз до поглъщането му при топлинна енергия.

Развитият в настоящата глава аналитичен апарат, базиран на дифузионно-възрастовото приближение, има следната най-важна особеност: пространственото разпределение на топлинните неутрони е навсякъде реактора е пропорционално на плътността на забавянето, т.е. на потока на надтоплинните неутрони. Ако се дефинира двугрупов неутронен спектър като F_th(r)/F_f(r), то той ще бъде независеща от координатите константа, определена единствено от материалния състава на размножаващата среда. Явно е, че тази принципна особеност на дифузионно-възрастовото уравнение го прави приложимо единствено за случая на хомогенен реактор без отражател. В хетерогенни среди - система от активна зона и отражател, елементарна реакторна клетка, решетка от условно хомогенизирани горивни касети с различни размножаващи свойства - неутронният спектър може да се отличава със силна зависимост от координатите. Така например, от прости физични съображения следва, че отношението F_th(r)/F_f(r) в активната зона ще нараства в близост до отражателя, а в него ще премине през пикова стойност в близост до активната зона. В околността на границата активна зона/отражател преносът на надтоплинни неутрони ще бъде главно по посока към отражателя, а на топлинни неутрони - по посока към активната зона. Подобна ще бъде и ситуацията около границата между две горивни касети, едната от които е с по-добри размножаващи свойства (по-висока стойност на k_¥) от другата Аналогични, но още по-силно проявени, са и явленията и процесите в системата горивна таблетка - забавител. Качествена представа за разпределението на двугруповия неутронен поток в реактор с отражател може да се придобие от долната фигура.

От изложеното по-горе е ясно, че описанието на хетерогенни среди (формулиране на условие за критичност, търсене на пространствени разпределения на потока) следва да се прави поне в многогрупово дифузионно приближение. Естествено, за моделиране на процесите в елементарната клетка и то не би било приложимо (виж Глава 3), но за случая на хомогенен реактор с отражател (или решетка от условно хомогенизирани горивни касети) се оказва достатъчно прилагането на двугруповата дифузионна теория. Докато при по-сложна реакторна геометрия, напр. решетка от условно хомогенизирани горивни касети, единственият приложим подход е численото решаване на системата от дифузионни уравнения (виж Глава 3 и Глава 6), за хомогенни реактори с отражател в прости геометрични конфигурации могат да бъдат приложени приблизителни аналитични методи, някои от които ще бъдат разгледани по-долу.

Въпреки приведените току-що аргументи в полза на многогруповия подход, в името на яснотата на разсъжденията първоначалните резултати ще бъдат получени в рамките на т.нар. едногрупова теория, т.е. ще се предполага, че възникването, дифузията и поглъщането на неутроните протичат само в топлинната група. Доколкото енергията на неутроните от делене се приема за топлинна, отпада необходимостта от описване на забавянето, а вероятността за избягване на резонансно залавяне p и коефициентът на размножение на бързите неутрони e ще бъдат по определение равни на единица. Така формулата на четирите множителя ще се сведе до .

Нека по-нататък индексите c и r се отнасят съответно за активната зона и за отражателя. Тогава стационарното дифузионно уравнение за неутроните в активната зона на критичния реактор ще придобие вида: . Или, след прегрупиране:. Въвеждайки критичния параметър получаваме вълновото уравнение за потока в активната зона: . (На практика за пресмятане на критичния параметър се предпочита изразът , но това не променя същността на разглежданията).

Тъй като отражателят няма размножаващи свойства, уравнението на дифузия за него ще бъде: . Или, , където .

За решаване на системата от две вълнови уравнения при съответните гранични условия, следващи от геометрията на реактора, е удобно да се разгледат случаи, които могат да се сведат до едномерни симетрични задачи - безкраен плосък слой, сфера и безкраен цилиндър. При това началото на координатната система ще бъде разположено съответно в равнината или центъра на симетрия.

а) Безкраен плосък слой

Нека безкрайният плосък слой с дебелина H е ограден двустранно с отражател с екстраполирана дебелина T. Ще разглеждаме само положителни стойности на x, защото поради симетрия за отрицателни стойности резултатите ще бъдат същите. Следвайки разсъжденията при аналогичната задача за реактор без отражател, може да се покаже, че решение на уравнението за неутронния поток в активната зона, удовлетворяващо условията за симетричност, крайност и неотрицателност, е , където A е произволна положителна константа. Тъй като k² е положителна реална величина, общото решение на уравнението за отражателя ще бъде: , където ;. От граничното условие следва, че и , където C е нова произволна положителна константа. Произволните константи A и C са свързани помежду си чрез граничното условие за непрекъснатост на потока и на тока на границата между активната зона и отражателя: . Първото от тези условия дава: , а второто - . Разделяйки второто на първото, получаваме критичното уравнение за реактора: . От него при известни материални свойства на средата (активна зона и отражател), може да се определи критичното съотношение между дебелината на активната зона H и дебелината на отражателя T.

б) Симетричен реактор със сферична активна зона и отражател

Следвайки вече разгледаните случаи, за потока в активната зона и в отражателя се получава: и . От условието за непрекъснатост на потока и на тока на границата между активната зона и отражателя се получава критичното уравнение . Както и в предходния случай, при известни материални свойства на средата то може да се използува за намиране на критичното съотношение между радиуса на активната зона R и дебелината на отражателя T.

И в двата разгледани случая, както и по принцип винаги, наличието на отражател намалява критичния обем на активната зона. Естествени изисквания към материала на отражателя са ниската маса на разсейващите ядра (тъй като в него попадат главно забавящи се неутрони), ниското сечение за поглъщане на неутрони и по възможност малката дължина на разсейване (последното при равни други условия увеличава геометричната вероятност за връщане на разсеяните в отражателя неутрони обратно в активната зона).

Нужно е обаче да се отбележи, че получените дотук едногрупови резултати са твърде приблизителни, тъй като не отчитат следните важни обстоятелства:

- поради добавъчните разсейващи удари в хода на забавянето им, попадналите в отражателя бързи неутрони с по-голяма вероятност могат да се върнат в активната зона, отколкото топлинните;

- неутроните с енергия над резонансната област при попадането си в отражателя се забавят там и след връщането си в активната зона избягват напълно резонансното залавяне (то протича главно в ²³⁸U).

Отчитането на тези обстоятелства, което може да стане едва в двугрупово приближение ще доведе до повишаване на ефективността на отражателя в сравнение с едногруповия случай.

Двугруповите дифузионни уравнения за системата активна зона + отражател могат да се запишат както следва. За надтоплинната група в активната зона: , където е сечението за извеждане на неутрони от бързата група, т.е. за процеса на преход от бързата в топлинната група поради забавяне чрез разсейващи удари, а е източникът на неутрони от делене в бързата група поради поглъщане на неутрони в топлинната група. За топлинната група в активната зона: . Източник на неутрони в топлинната група е скоростта на извеждане на неутрони от бързата, т.е. поглъщането в процеса на забавяне се пренебрегва. В този смисъл, изразът за k_¥ също не трябва да отчита резонансното поглъщане. За надтоплинната група в отражателя: . Източник в това уравнение няма, защото отражателят е неразмножаваща среда, а се дефинира напълно аналогично на . За топлинната група в отражателя: . Уравнението е аналогично на това за топлинната група в активната зона.

Тази система от четири дифузионни уравнения се решава съвместно при спазване на външното гранично условие за свободна повърхност и вътрешното гранично условие за непрекъснатост на тока и потока, и, естествено при спазване на изискването за крайност и неотрицателност на всички неутронни потоци.

Всички уравнения, с изключение на това за бързата група в отражателя, са нехомогенни. Техните хомогенни части, обаче, имат вида на вълнови уравнения. В този смисъл, за дифузионните уравнения в активната зона могат да се търсят решения, удовлетворяващи: и , както и условията, при които решенията на тези вълнови уравнения ще бъдат решения и на дифузионните уравнения. Еднаквостта на константата B² за двете уравнения се обосновава по следния начин: Ако от уравнението за топлинната група се изрази чрез и се замести в уравнението за бързата група, ще се получи съотношение, съдържащо само . И обратно, изразявайки чрез от уравнението за бързата група и замествайки в това за топлинната група, ще се получи съотношение само за , съвпадащо по форма с предходното. Следователно, ако хомогенните части бъдат представени като вълнови уравнения, B² трябва да бъде еднакво за двата случая.

След заместване на лапласианите в двете дифузионни уравнения за активната зона съответно с и , се получава: .

Тази линейна система за и (в която B² е подлежащ на определяне параметър) ще има нетривиално решение само ако детерминантата на нейните коефициенти е нула: . Или, след прегрупиране: , където Доколкото в действителност е сечението за забавяне до топлинна енергия, може да се покаже, че , където е средният квадрат на разстоянието, изминато по права линия от неутрона в процеса на забавянето му до топлинна енергия. Следователно, , където е възрастта на топлинните неутрони в активната зона, така че се получава еквивалентният запис: . Това е характеристичното уравнение за активната зона на реактор с отражател в двугрупово приближение. То съвпада по форма с двугрупoвото критично уравнение за реактор без отражател и е подобно на критичното уравнение за голям реактор в дифузионно-възрастово приближение. Тъй като , и са материални характеристики на размножаващата среда, това уравнение дава допустимите стойности на B², при които решенията на двугруповото дифузионно уравнение за активната зона имат вида на решения на вълновото уравнение. Характеристичното уравнение е от втора степен относно B², така че то има следните две решения:

.

Нека решенията на вълновото уравнение, съответствуващи на m² и -n² са X(r) и Y(r), т.е. и . Решенията на тези уравнения ще зависят от геометрията на реактора. Ограничавайки се, както и преди, със случаи, свеждащи се до симетрични едномерни задачи, се получават следните форми на X и Y, удовлетворяващи условията за крайност, неотрицателност и симетричност:

Решения на вълновите уравнения за неутронния поток в активната зона

Геометрия	X	Y
Безкраен слой
Сфера
Безкраен цилиндър

Общите решения на двугруповото дифузионно уравнение за активната зона са линейни комбинации на X и Y: и . Тъй като са допустими и решенията и , то . Замествайки в дифузионното уравнение за топлинната група: . Или: . Аналогично, след замяната , и , дифузионното уравнение за топлинната група придобива вида: . Следователно: . Вижда се, че S₁ и S₂ не са произволни константи, така че общите решения на двугруповото дифузионно уравнение за активната зона ще бъдат: и .

Двугруповото дифузионно уравнение за отражателя може да се запише във вида: и , където и . Първото уравнение може да се реши пряко, тъй като има вида на вълново уравнение. След замяна на с неговото решение ще бъде и решение на хомогенната част на второто уравнение. Допустимите решения Z на това вълново уравнение, намерени при гранично условия за нулев поток на външната екстраполирана граница на отражателя, за разглежданите три геометрии, са:

Решения на вълновото уравнение за неутронния поток в отражателя

Геометрия	Z	Z при T ® ¥
Безкраен слой
Сфера
Безкраен цилиндър

Нека Z_f е решението на вълновото уравнение с k_f,r, а Z_th - решението с k_th,r. Тогава общото решение на дифузионното уравнение за бързата група ще има вида: , а на дифузионното уравнение за топлинната група - , където F и G са произволни константи, а S₃ се определя по следния начин: Замествайки общото решение за в дифузионното уравнение за топлинната група (членът може да не се включва, защото е решение на хомогенната част и приносът му ще бъде нулев) и отчитайки, че , се получава: . Или: .

Решенията на двугруповите дифузионни уравнения за активната зона и за отражателя съдържат общо четири подлежащи на определяне параметъра: A, C, F и G. За намирането им трябва да се удовлетворят общо четирите вътрешни гранични условия - за непрекъснатост на потока и на тока на бързите и на топлинните неутрони на границата между активната зона и отражателя: , където X’, Y’, Z’_f и Z’_th са първите производни по x или r на X, Y, Z_f и Z_th, а всички зависещи от координатите величини са пресметнати на границата между активната зона и отражателя.

Решението на тази хомогенна линейна система относно A, C, F и G ще бъде нетривиално, ако детерминантата на коефициентите пред тях е равна на нула: .

Това условие има смисъл на критично уравнение за реактор в отражател в рамките на разглежданото двугрупово приближение. При известни материални свойства на активната зона и на отражателя и при избрана форма на реактора то може да се използува за намиране на критичното съотношение между размера на активната зона и размера на отражателя. Даже и при най-простия възможен вид на координатните зависимости на решенията на вълновите уравнения то представлява сложно трансцедентно уравнение относно търсените критични размери, поради винаги се решава числено.