6. Физични особености
на хетерогенните среди. Основни понятия от теорията на решетките. Методи за
определяне на критичното състояние на хетерогенни реактори. Методи за
неутронно-физично пресмятане на реакторите. Програмни продукти.
Обобщавайки изложеното в предходната глава, следва да се отбележи, че въведеният там аналитичен апарат по принцип позволява разглеждания на всякакви хетерогенни структури. На практика обаче, математичните затруднения свеждат неговата приложимост само до прости системи от хомогенни области. Хетерогенната структура на тези хомогенни области в рамките на въведените модели се отчита неявно чрез дефинирания в Глава 4 коефициент на размножение за безкрайна решетка k¥. Принципите за неговото пресмятане за хетерогенни реакторни среди, както и действително прилаганите методи за числено пресмятане на неутронно-физичните характеристики на реалните реактори, ще бъдат разгледани по-долу.
Преди да пристъпим към по-детайлен анализ на начините на отчитане на хетерогенната структура при моделиране на неутронно-физичните процеси в ядрените реактори, е уместно да се направи просто качествено разглеждане на ефектите от пространственото разделяне на горивото от забавителя върху размножаващите свойства на реакторите с топлинни неутрони. За целта ще се интересуваме от промените във всеки от четирите множителя на k¥ при прехода от хомогенна към хетерогенна среда.
Именно на основата на такова разглеждане са били обосновани основните конструкционни принципи на първия в света реактор на топлинни неутрони с гориво от природен уран и графитов забавител, построен от Ферми в Чикагския университет през 1942 г. Мотивация за търсенето на особена конструкция на активната зона е обстоятелството, че достигане на критичност в хомогенен уран-графитов реактор с природен уран е невъзможно. Тъй като за природен уран h » 1.33, e » 1.05, а максималната стойност на произведението pf за хомогенна смес от природен уран и графит е » 0.59, то най-голямата достижима стойност на k¥ ще бъде около 0.85. Търсейки решение на проблема, Ферми и Сцилард забелязват, че вероятността за избягване на резонансно поглъщане p може да бъде значително повишена чрез пространствено разделяне на горивото от забавителя. Това е така, защото неутроните, достигнали в забавителя резонансни енергии, се поглъщат основно във външния слой на горивния елемент и почти не достигат вътрешността му. Пространственото самоекраниране на горивния елемент от резонансни неутрони води до общо намаляване на скоростта на резонансно поглъщане. (Това явление е тясно свързано с енергетичното самоекраниране, коментирано в Глава 4 по повод на т.нар. доплеров ефект). Ефектът е от пространственото самоекраниране е толкова силен, че стойността на k¥ в хетерогенната решетка на реактор с графит и природен уран може да достигне 1.08.
Хетерогенната структура обаче води и до други ефекти, някои от които също благоприятни, а други - не. Сред благоприятните ефекти е лекото повишаване на коефициента на размножение на бързите неутрони e, дължащо се на относително по-голямата вероятност за взаимодействие на бързи неутрони с ядрата на горивото. Неблагоприятен ефект е известното намаляване на коефициента на използуване на топлинните неутрони f, причинено от спадането на потока на топлинните неутрони във вътрешността на горивния елемент, водещо до общо относително намаляване на скоростта на поглъщане на топлинни неутрони в горивото. Този ефект, обаче, се компенсира с голям излишък от повишаването на p.
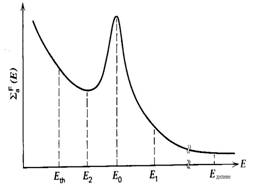
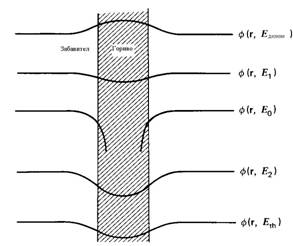
За илюстриране на казаното дотук, на долната фигура е показана формата на неутронния поток при различни енергии в елементарната клетка на реактора.
Нека сега разгледаме малко по-подробно влиянието на
хетерогенността върху всеки от множителите на ![]()
Коефициентът на размножение на топлинните неутрони h
зависи само от макроскопичните сечения на горивото: 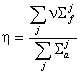 . Тъй като тези сечения зависят от спектъра на топлинните
неутрони, който на свой ред се обуславя от конфигурацията на хетерогенната
решетка, множителят h
ще се мени, макар и слабо, с вариране на диаметъра на горивния елемент и на
стъпката на решетката. Количественото описание на това изменение, обаче,
изисква сложен аналитичен апарат и е извън кръга на нашите разглеждания.
. Тъй като тези сечения зависят от спектъра на топлинните
неутрони, който на свой ред се обуславя от конфигурацията на хетерогенната
решетка, множителят h
ще се мени, макар и слабо, с вариране на диаметъра на горивния елемент и на
стъпката на решетката. Количественото описание на това изменение, обаче,
изисква сложен аналитичен апарат и е извън кръга на нашите разглеждания.
Коефициентът на използуване на топлините неутрони в
елементарната клетка на реактора е: 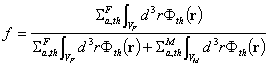 , където с “F” и “M” се бележат съответно горивото и
забавителят. Нека средните стойности на потока на топлинните неутрони във всяка
от тези две области са:
, където с “F” и “M” се бележат съответно горивото и
забавителят. Нека средните стойности на потока на топлинните неутрони във всяка
от тези две области са: ![]() и
и ![]() . Въвеждайки т.нар. коефициент
на загуба за топлинните неутрони:
. Въвеждайки т.нар. коефициент
на загуба за топлинните неутрони: ![]() , се получава:
, се получава: 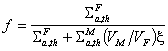 . Тъй като, очевидно, x > 1, а при
равни други условия стойността на f за хомогенна среда със същия
материален състав ще се дава от горния израз, но при x = 1, то
. Тъй като, очевидно, x > 1, а при
равни други условия стойността на f за хомогенна среда със същия
материален състав ще се дава от горния израз, но при x = 1, то ![]() .
.
Приблизителен израз за коефициента f може да се получи в рамките на дифузионната теория при следните допълнителни допускания:
- Тъй като височината на елементарната клетка е много по-голяма от напречния й размер, задачата може да се сведе до двумерна. По-нататък, отчитайки че горивният елемент е цилиндричен и условно апроксимирайки външната граница на елементарната клетка с цилиндрична повърхност (така че обемът на забавителя да съвпада с действителния), задачата се свежда до едномерна, с единствена променлива разстоянието r от центъра на клетката.
- Предполагаме също, че плътността на забавяне в забавителя не зависи от координатите, а в горивото е равна на нула. Така уравнението на дифузия ще може да се запише само за топлинните неутрони.
В горивния обем то ще бъде ![]() . Съгласно предположението за нулева плътност на забавянето
(т.е. отсъствие на забавяне) в горивото, в това уравнение няма член, описващ
източника на топлинните неутрони. В обема на забавителя дифузионното уравнение
е
. Съгласно предположението за нулева плътност на забавянето
(т.е. отсъствие на забавяне) в горивото, в това уравнение няма член, описващ
източника на топлинните неутрони. В обема на забавителя дифузионното уравнение
е ![]() , където q е броят
неутрони в 1 cm3 от материала на забавителя, достигащи за
1 sec топлинни енергии. Съгласно предположението за хомогенна плътност на
забавянето, q = const.
Решението на тази система от диференциални уравнения трябва да удовлетворява
следните гранични условия:
, където q е броят
неутрони в 1 cm3 от материала на забавителя, достигащи за
1 sec топлинни енергии. Съгласно предположението за хомогенна плътност на
забавянето, q = const.
Решението на тази система от диференциални уравнения трябва да удовлетворява
следните гранични условия:
- непрекъснатост на потока на границата гориво/забавител: ![]() , където R0
е външният радиус на горивния елемент;
, където R0
е външният радиус на горивния елемент;
- непрекъснатост на тока през границата гориво/забавител: ![]() ;
;
- нулев ток през външната граница на елементарната клетка: ![]() , където R1
е външният радиус на елементарната клетка. Това условие е израз на твърдението,
че решетката от елементарни клетки е безкрайна.
, където R1
е външният радиус на елементарната клетка. Това условие е израз на твърдението,
че решетката от елементарни клетки е безкрайна.
Уравнението за горивната област е вълново: ![]() , където
, където ![]() . Или, в цилиндрични координати:
. Или, в цилиндрични координати: ![]() . Неговото общо решение е
. Неговото общо решение е ![]() . Тъй като
. Тъй като ![]() при
при ![]() , то
, то ![]() . Уравнението за забавителя се представя във вида:
. Уравнението за забавителя се представя във вида: ![]() , където
, където ![]() . Хомогенната част на това уравнение е аналогична на горното
и решението й е:
. Хомогенната част на това уравнение е аналогична на горното
и решението й е: ![]() . Функцията K0
не може да бъде отхвърлена, защото областта на забавителя не включва r = 0. Частно решение на
дифузионното уравнение за забавителя може да се получи, полагайки
. Функцията K0
не може да бъде отхвърлена, защото областта на забавителя не включва r = 0. Частно решение на
дифузионното уравнение за забавителя може да се получи, полагайки ![]() :
: ![]() . Тогава общото решение на това уравнение ще бъде
. Тогава общото решение на това уравнение ще бъде ![]() . Отношението между произволните константи C и F
се получава от третото гранично условие:
. Отношението между произволните константи C и F
се получава от третото гранично условие: ![]() , т.е.
, т.е. ![]() . Константите A и C могат да бъдат определени от
останалите две гранични условия. За по-нататъшните разглеждания обаче
стойността на C не е нужна, а вместо
с A е по-удобно да се работи с
реципрочната й стойност:
. Константите A и C могат да бъдат определени от
останалите две гранични условия. За по-нататъшните разглеждания обаче
стойността на C не е нужна, а вместо
с A е по-удобно да се работи с
реципрочната й стойност: 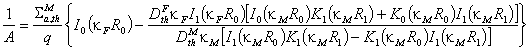 .
.
Използувайки получените резултати, пълният брой топлинни
неутрони поглъщани за 1 sec на единица височина от горивния елемент може
да се пресметне като: ![]() . Броят топлинни неутрони, образуващи се за 1 sec в
единица обем от забавителя, е равен на q,
а на единица височина от забавителя -
. Броят топлинни неутрони, образуващи се за 1 sec в
единица обем от забавителя, е равен на q,
а на единица височина от забавителя - ![]() . В критично състояние този брой е равен на броя топлинни
неутрони, поглъщани за 1 sec на единица височина от елементарната клетка,
т.е. на знаменателя на израза за f.
Следователно,
. В критично състояние този брой е равен на броя топлинни
неутрони, поглъщани за 1 sec на единица височина от елементарната клетка,
т.е. на знаменателя на израза за f.
Следователно, ![]() .
.
В Глава 4 беше получен следният общ приблизителен израз за
вероятността за избягване на резонансно поглъщане p: 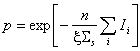 , където n е
ядрената концентрация на резонансния поглътител, а
, където n е
ядрената концентрация на резонансния поглътител, а ![]() са индивидуалните
резонансни интеграли. Начинът на неговото получаване предполагаше т.нар.
“безкрайно разреждане”, т.е. липса на всякакво енергетично или пространствено
самоекраниране. Очевидно това предположение е напълно погрешно за хетерогенната
елементарна клетка на реалния реактор, така че в тази ситуация приведеният
израз за p е напълно неприложим. Така
например, ако резонансният интеграл за дадена хомогенна смес от природен уран и
забавител е 280 b, то при подходящо пространствено разделяне на урана от
забавителя неговата стойност намалява до 9 b, т.е. повече от 30 пъти! В
действителност, за количествено оценяване на коефициента p в хетерогенна решетка се прибягва до сложен аналитичен апарат,
който е извън рамките на това изложение. Крайният резултат от такъв анализ,
записан по отношение на т.нар. ефективен
резонансен интеграл, приложим в изрази формално подобни на въведения за
безкрайно разреждане, има типичния вид:
са индивидуалните
резонансни интеграли. Начинът на неговото получаване предполагаше т.нар.
“безкрайно разреждане”, т.е. липса на всякакво енергетично или пространствено
самоекраниране. Очевидно това предположение е напълно погрешно за хетерогенната
елементарна клетка на реалния реактор, така че в тази ситуация приведеният
израз за p е напълно неприложим. Така
например, ако резонансният интеграл за дадена хомогенна смес от природен уран и
забавител е 280 b, то при подходящо пространствено разделяне на урана от
забавителя неговата стойност намалява до 9 b, т.е. повече от 30 пъти! В
действителност, за количествено оценяване на коефициента p в хетерогенна решетка се прибягва до сложен аналитичен апарат,
който е извън рамките на това изложение. Крайният резултат от такъв анализ,
записан по отношение на т.нар. ефективен
резонансен интеграл, приложим в изрази формално подобни на въведения за
безкрайно разреждане, има типичния вид: ![]() , където SF
е повърхностната площ на горивния елемент, MF
е неговата маса, а C1 и C2 са специално подбрани
константи.
, където SF
е повърхностната площ на горивния елемент, MF
е неговата маса, а C1 и C2 са специално подбрани
константи.
Един приблизителен подход за оценяване на p, предложен първоначално от Вигнер и
подобен на приложения по-горе за f,
се състои в следното. Нека условно представим ефективното сечение за резонансно
поглъщане в горивния блок по следния начин: ![]() , където първият член отдясно има смисъл на “сечение за
обемно поглъщане”, вторият - на “сечение за повърхностно поглъщане”, а SF и MF са определени по-горе. При известни, напр. емпирично
оценени, стойности на a(E) и b(E), и следвайки логиката на
разсъжденията в Глава 4, за вероятността за избягване на резонансно поглъщане
се получава изразът:
, където първият член отдясно има смисъл на “сечение за
обемно поглъщане”, вторият - на “сечение за повърхностно поглъщане”, а SF и MF са определени по-горе. При известни, напр. емпирично
оценени, стойности на a(E) и b(E), и следвайки логиката на
разсъжденията в Глава 4, за вероятността за избягване на резонансно поглъщане
се получава изразът: 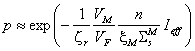 . Тук VM
и VF са обемите на
забавителя и на горивото, n (както и
по-горе) е ядрената концентрация на резонансния поглътител в горивото, xM
е средната логаритмична загуба на енергия при един разсейващ удар в забавителя,
. Тук VM
и VF са обемите на
забавителя и на горивото, n (както и
по-горе) е ядрената концентрация на резонансния поглътител в горивото, xM
е средната логаритмична загуба на енергия при един разсейващ удар в забавителя,
![]() е макроскопичното
сечение за разсейване в забавителя,
е макроскопичното
сечение за разсейване в забавителя, ![]() е коефициентът на загуба за неутрони в резонансната област, а
е коефициентът на загуба за неутрони в резонансната област, а ![]() е ефективният
резонансен интеграл. Следователно, при известни материални константи, геометрия
на елементарната клетка и ефективен резонансен интеграл, за пресмятане на p е нужно да се определи единствено
коефициентът на загуба zr. Последното може да стане в едногрупово
дифузионно приближение за енергията на резонансните неутрони по начин, напълно
аналогичен на използувания по-горе за пресмятане на множителя f. В този смисъл, тъй като в горивото
забавянето е пренебрежимо малко, може да се приеме, че източникът на резонансни
неутрони е равномерно разпределен в обема на забавителя. Нека също така
приемем, че материалните константи за резонансната група в горивото и
забавителя,
е ефективният
резонансен интеграл. Следователно, при известни материални константи, геометрия
на елементарната клетка и ефективен резонансен интеграл, за пресмятане на p е нужно да се определи единствено
коефициентът на загуба zr. Последното може да стане в едногрупово
дифузионно приближение за енергията на резонансните неутрони по начин, напълно
аналогичен на използувания по-горе за пресмятане на множителя f. В този смисъл, тъй като в горивото
забавянето е пренебрежимо малко, може да се приеме, че източникът на резонансни
неутрони е равномерно разпределен в обема на забавителя. Нека също така
приемем, че материалните константи за резонансната група в горивото и
забавителя, ![]() ,
, ![]() ,
, ![]() и
и ![]() са известни (напр.
оценени с използуване на експериментални данни). Тогава, системата от
дифузионни уравнения за резонансните неутрони в елементарната клетка ще бъде:
са известни (напр.
оценени с използуване на експериментални данни). Тогава, системата от
дифузионни уравнения за резонансните неутрони в елементарната клетка ще бъде: ![]() и
и ![]() , където
, където ![]() и
и ![]() , а
, а ![]() , където qr
е източникът на резонансни неутрони в забавителя. Граничните условия са същите
като при съответните уравнения, използувани по-горе за пресмятане на f. Решавайки тези уравнения по познатия
вече начин, напълно аналогично на коефициента на използуване на топлинни
неутрони f може да се пресметне коефициент на използуване на резонансните
неутрони fr º “брой
на неутроните, погълнати в резонансите на урана”/(“брой на резонансните
неутрони, образуващи се в елементарната клетка”. Така, следвайки приведения
по-горе израз за коефициента f, за
коефициента на загуба на резонансни неутрони окончателно се получава:
, където qr
е източникът на резонансни неутрони в забавителя. Граничните условия са същите
като при съответните уравнения, използувани по-горе за пресмятане на f. Решавайки тези уравнения по познатия
вече начин, напълно аналогично на коефициента на използуване на топлинни
неутрони f може да се пресметне коефициент на използуване на резонансните
неутрони fr º “брой
на неутроните, погълнати в резонансите на урана”/(“брой на резонансните
неутрони, образуващи се в елементарната клетка”. Така, следвайки приведения
по-горе израз за коефициента f, за
коефициента на загуба на резонансни неутрони окончателно се получава: 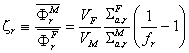 . Или, за вероятността за избягване на резонансно поглъщане:
. Или, за вероятността за избягване на резонансно поглъщане: 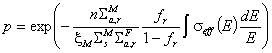 . По силата на връзки между участвуващите в този израз
материални константи, които следват от специфичния начин на тяхното дефиниране,
и които тук за краткост ще пропуснем, се оказва, че за p е в сила простият израз:
. По силата на връзки между участвуващите в този израз
материални константи, които следват от специфичния начин на тяхното дефиниране,
и които тук за краткост ще пропуснем, се оказва, че за p е в сила простият израз: 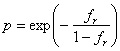 .
.
Както беше споменато по-горе, коефициентът на размножение на
бързите неутрони e
в хетерогенния реактор е по-голям от съответния му за еквивалентна хомогенна
смес. По ясни физични съображения той ще нараства с увеличаване на отношението ![]() в елементарната
клетка. Може сравнително лесно да се покаже, че
в елементарната
клетка. Може сравнително лесно да се покаже, че 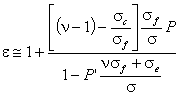 , където sf, se, sc
и s
са съответно сечението за делене, за еластично разсейване, за залавяне (не
водещо до делене) и за пълно взаимодействие на 238U за енергия на
неутроните над прага на делене, P е
вероятността за взаимодействие на първичен бърз неутрон от делене с ядро на 238U
в горивния блок, а P’ е вероятността
за взаимодействие на бърз неутрон от второ или следващо поколение с ядро на 238U
в горивния блок. Доколкото, следвайки разсъжденията в Глава 1, може да се
покаже, че вероятността неутрон, възникнал в точка r1, да взаимодействува с ядро в елементарния обем dV2 около точката r2 е
, където sf, se, sc
и s
са съответно сечението за делене, за еластично разсейване, за залавяне (не
водещо до делене) и за пълно взаимодействие на 238U за енергия на
неутроните над прага на делене, P е
вероятността за взаимодействие на първичен бърз неутрон от делене с ядро на 238U
в горивния блок, а P’ е вероятността
за взаимодействие на бърз неутрон от второ или следващо поколение с ядро на 238U
в горивния блок. Доколкото, следвайки разсъжденията в Глава 1, може да се
покаже, че вероятността неутрон, възникнал в точка r1, да взаимодействува с ядро в елементарния обем dV2 около точката r2 е ![]() , вероятностите P и P’ могат да бъдат пресметнати по данни
за формата и размера на горивния блок.
, вероятностите P и P’ могат да бъдат пресметнати по данни
за формата и размера на горивния блок.
За илюстриране на казаното дотук за четирите множителя на ![]() в хетерогенна среда,
на долната фигура е показана зависимостта на тези множители от хетерогенността
(измервана в случая с отношението на стъпката на решетката към диаметъра на
горивния елемент) за реактор от типа PWR (т.е., в частност, ВВЕР).
в хетерогенна среда,
на долната фигура е показана зависимостта на тези множители от хетерогенността
(измервана в случая с отношението на стъпката на решетката към диаметъра на
горивния елемент) за реактор от типа PWR (т.е., в частност, ВВЕР).
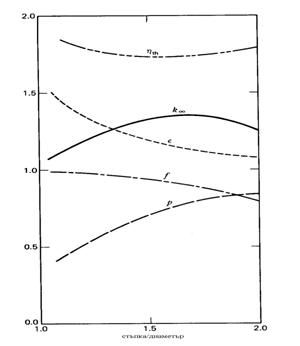
Завършвайки изложението, посветено на основните принципи за
определяне на ![]() в хетерогенна среда, е
уместно да се напомни, че по-нататъшният приблизителен анализ на хетерогенния
реактор с крайни граници може да се проведе изцяло в рамките на развитите в
предходната глава методи.
в хетерогенна среда, е
уместно да се напомни, че по-нататъшният приблизителен анализ на хетерогенния
реактор с крайни граници може да се проведе изцяло в рамките на развитите в
предходната глава методи.
В действителност, обаче, повечето от разгледаните в тази и предходните глави аналитични методи за определяне на неутронно-физичните характеристики в ядрените реактори имат само историческа и учебно-методическа стойност. Първоначално разработени за реактори с графитен забавител и гориво от природен уран, а по-късно усложнявани и адаптирани ad hoc за други типове реактори, вкл. и за PWR (ВВЕР), те са били ограничени от липсата на изчислителни ресурси и на специализирани числени методи за по-точно решаване на уравнението на неутронния пренос, както и на детайлни знания за неутронните сечения. Тъй като получаваните при тяхното прилагане резултати не отговарят на съвременните изисквания за точност, те отдавна не се прилагат за реални неутронно-физични пресмятания. Естествено, тяхното включване в настоящото изложение за целите на въвеждането в общите принципи на реакторния анализ, е напълно оправдано.
В Глава 3 бяха изложени общите принципи за пряко числено решаване на уравнението на неутронния пренос. Пак там беше показано, че последователното прилагане на тези принципи за реалната хетерогенна геометрия на активната зона изисква огромни изчислителни разходи и все още е практически нецелесъобразно. От друга страна, при подходящо дефинирани групови константи (дифузионни коефициенти, макроскопични сечения и гранични условия) граничната задача за активната зона може с малки изчислителни разходи и със задоволителна точност да се реши в едроклетъчно малогрупово (най-често двугрупово) дифузионно приближение, а получените пространствени разпределения на скаларния поток и на скоростите на неутронните реакции позволяват описание на всички важни от експлоатационна гледна точка неутронно-физични характеристики на активната зона. Следователно, ключов въпрос е дали общата задача за решаване на уравнението на неутронния пренос (наричано за краткост транспортно уравнение) може да се раздели на два етапа - а) пресмятане на нужните групови дифузионни константи, и б) използуване на тези константи за решаване на едроклетъчната двугрупова дифузионна гранична задача за активната зона. Ако такова разделяне е възможно, то потенциално големите изчислителни разходи за първия етап не биха били толкова ограничаващи, защото за даден тип и конструкция на реактора генерирането на константите ще се прави само веднъж, докато пресмятанията на втория етап по необходимост се провеждат многократно в хода на експлоатацията на всеки ядрен реактор.
Отговорът на поставения въпрос ще се обуславя от основното
изискване към търсените групови константи: 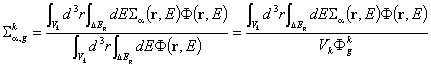 или
или 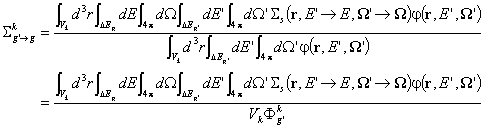 , където a = t, а, s, f, tr,... е типът на описваната реакция
(процес), g е енергетичната група, a k е номерът на пространствената област (нод) с обем Vk. Ясно е, че горните изрази, представляващи
определения за груповите едроклетъчни константи
, където a = t, а, s, f, tr,... е типът на описваната реакция
(процес), g е енергетичната група, a k е номерът на пространствената област (нод) с обем Vk. Ясно е, че горните изрази, представляващи
определения за груповите едроклетъчни константи ![]() и
и ![]() , са изисквания за запазване на скоростта на съответните
реакции при енергетична и пространствена дискретизация. Също така, нодалните
групови потоци
, са изисквания за запазване на скоростта на съответните
реакции при енергетична и пространствена дискретизация. Също така, нодалните
групови потоци ![]() трябва да съвпадат с
решението на едроклетъчното дифузионно уравнение. Доколкото реалните нодове
(типично съответствуващи на призматични слоеве от горивни касети) са
хетерогенни, въведените определения се и предписания за тяхната условна
хомогенизация.
трябва да съвпадат с
решението на едроклетъчното дифузионно уравнение. Доколкото реалните нодове
(типично съответствуващи на призматични слоеве от горивни касети) са
хетерогенни, въведените определения се и предписания за тяхната условна
хомогенизация.
От необходимостта от познаване на действителното решение на транспортното уравнение за получаване на нодалните групови константи формално следва, че отговорът на въпроса за възможността за разделяне на решаването на транспортното уравнение на два етапа трябва да бъде отрицателен. В действителност това обаче не е така, защото в рамките на нода неутронният спектър в подходящо обособената енергетична група g се определя главно от неговите материални свойства и зависи слабо от външното му обкръжение. Следователно, задачата за пресмятане на нодалните групови константи може да се реши за безкрайна периодична решетка от касети (или даже елементарни реакторни клетки). На практика това означава ограничаване на разглежданията до слой от една касета или елементарна клетка и свеждане на пространствената зависимост до едномерна (или двумерна). Често се оказва възможно прилагането на интегрални преобразования (от типа на лапласовите) и представяне на члена на утечките по начин, подобен на този във вече разгледаното вълново уравнение, така че явната зависимост от координатите може напълно да се елиминира. Енергетичната зависимост и анизотропията на сеченията и на насочената плътност на потока, за сметка на това, се описват детайлно. Това означава въвеждане на десетки или стотици енергетични групи и представяне на зависимостта от посоката на движение на неутроните W чрез разлагане по базови функции (PL приближениe) и/или чрез дискретизация (метод на дискретните ординати (SN приближение), метод на характеристиките и др.). За намаляване на изчислителните разходи и/или повишаване на точността на резултатите, в математичните модели могат да се включат и аналитични елементи, подобни на разгледаните в тази и предходните глави. Доколкото главната цел на този тип пресмятания е да се моделират вътрешногруповите неутронни спектри, е прието те да се наричат спектрални. Примери за съвременни програмни комплекси за спектрални пресмятания са WIMS, Helios, Casmo. Прилаганите методики са специфични и разнообразни, но тъй като спектралните пресмятания се ограничават до първия от обособените два етапа за решаване на транспортното уравнение и решаваните чрез тях задачи са практически независими от тези на експлоатационните пресмятания на неутронно-физичните характеристики на активната зона, те няма да бъдат предмет на настоящето изложение.
Явно е, че материалните характеристики на нода ще зависят от параметрите на състоянието на активната зона (дълбочина на изгаряне, борна концентрация, мощност, входна температура и разход на топлоносителя и т.н.). Поради това спектралните пресмятания се провеждат за различни комбинации на тези параметри на състоянието, а натрупаната база от данни за нодалните групови константи, наречена библиотека, се организира по подходящ начин, така че на етапа на експлоатационните пресмятания от нея да бъдат извличани нужните константи за всеки нод и във всяко състояние на реактора.
Приемайки, че всички коефициенти и гранични условия са вече
налице, ограничавайки се до условно-критичната задача, но засега не и до
частния случай на две енергетични групи, подлежащото на решаване многогрупово
дифузионно уравнение ще бъде (виж Глава 3): 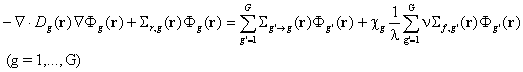 , където
, където ![]() е сечението за извеждане от група g.
е сечението за извеждане от група g.
Тъй като надтоплинните неутрони не могат да придобиват
енергия при разсейване, ако всички топлинни неутрони бъдат обединени в една
група (като правило с горна граница 0.625 eV), източникът на неутрони от
разсейване ще бъде ![]() . (Тук е уместно да се напомни, че номерацията на групите е в
посока на намаляване на енергията). По-нататъшните разглеждания ще се отнасят
именно за този случай, но крайните резултати се обобщават пряко и за произволно
енергетично разбиване. Ако също така приемем, че източникът на неутрони от
делене
. (Тук е уместно да се напомни, че номерацията на групите е в
посока на намаляване на енергията). По-нататъшните разглеждания ще се отнасят
именно за този случай, но крайните резултати се обобщават пряко и за произволно
енергетично разбиване. Ако също така приемем, че източникът на неутрони от
делене ![]() е оценен предварително
(напр. по предходно приближение на груповите потоци), то всяко уравнение от
горната система може да се реши отделно от останалите, стига това да става в
реда g = 1, g = 2, ..., g = G.
е оценен предварително
(напр. по предходно приближение на груповите потоци), то всяко уравнение от
горната система може да се реши отделно от останалите, стига това да става в
реда g = 1, g = 2, ..., g = G.
И така, дифузионното уравнение за група g ще има вида ![]() , където източникът
, където източникът ![]() е вече известен.
Въвеждайки пространствена дискретизация, така че всички граници между условно
хомогенизираните участъци от реакторната среда да съвпадат с граници между
нодове, и едноиндексна номерация на нодовете (напр. отгоре надолу, отвън
навътре и отляво надясно), то след интегриране по нодове и разделяне на техните
обеми Vk дифузионното уравнение за група g се представя като следната система от
балансни уравнения:
е вече известен.
Въвеждайки пространствена дискретизация, така че всички граници между условно
хомогенизираните участъци от реакторната среда да съвпадат с граници между
нодове, и едноиндексна номерация на нодовете (напр. отгоре надолу, отвън
навътре и отляво надясно), то след интегриране по нодове и разделяне на техните
обеми Vk дифузионното уравнение за група g се представя като следната система от
балансни уравнения: ![]() , където груповият индекс g
е изпуснат, а членът на утечките е преобразуван с използуване на теоремата за
дивергенцията (на Гаус-Остроградски). Сумирането по k’ обхваща нодовете, с които нодът k има обща стена, а токовете през тези общи стени са
, където груповият индекс g
е изпуснат, а членът на утечките е преобразуван с използуване на теоремата за
дивергенцията (на Гаус-Остроградски). Сумирането по k’ обхваща нодовете, с които нодът k има обща стена, а токовете през тези общи стени са ![]() . Източникът
. Източникът ![]() е, разбира се,
известен, а нодалните групови потоци
е, разбира се,
известен, а нодалните групови потоци ![]() подлежат на
определяне. Явно е, че за да може получената система от балансни уравнения да
бъде решена относно нодалните потоци Fk, трябва да
бъде намерен начин за изразяване на токовете
подлежат на
определяне. Явно е, че за да може получената система от балансни уравнения да
бъде решена относно нодалните потоци Fk, трябва да
бъде намерен начин за изразяване на токовете ![]() чрез тях. Съществуват
разнообразни начини за въвеждане на търсените връзки, общоприето наричани нодални модели. Оставяйки описанието и
класификацията на нодалните модели извън кръга на настоящите разглеждания, тук
ще се ограничим само с най-простия от тях, и то започвайки с едномерния случай,
т.е. пространствена зависимост единствено от координатата x.
чрез тях. Съществуват
разнообразни начини за въвеждане на търсените връзки, общоприето наричани нодални модели. Оставяйки описанието и
класификацията на нодалните модели извън кръга на настоящите разглеждания, тук
ще се ограничим само с най-простия от тях, и то започвайки с едномерния случай,
т.е. пространствена зависимост единствено от координатата x.
Нека xk-1,
xk и xk+1 са координатите на центровете на три съседни нода
(имащи в случая формата на безкрайни плоскопаралелни слоеве), a ![]() и
и ![]() са координатите на
лявата и дясната граница на нода k
(общи съответно с нода k-1 и k+1. Нека също така всички нодове са с
еднаква ширина h. В този случай
нормалните компоненти на тока през лявата и дясната стени на нода k ще бъдат съответно
са координатите на
лявата и дясната граница на нода k
(общи съответно с нода k-1 и k+1. Нека също така всички нодове са с
еднаква ширина h. В този случай
нормалните компоненти на тока през лявата и дясната стени на нода k ще бъдат съответно ![]() и
и ![]() . Прилагайки стандартното представяне на производните чрез
крайни разлики,
. Прилагайки стандартното представяне на производните чрез
крайни разлики, ![]() , и приемайки, че потокът в центъра на нода съвпада със
средната му стойност, т.е. напр.
, и приемайки, че потокът в центъра на нода съвпада със
средната му стойност, т.е. напр. ![]() , бихме получили:
, бихме получили: ![]() и
и ![]() , където
, където ![]() и
и ![]() са стойностите на
потока на лявата и дясната граница на нода k.
Докато непрекъснатостта на потока на границата между нода k и неговите съседи се осигурява от самото дефиниране на тези
гранични потоци, техните стойности се намират от условията за непрекъснатост на
тока на границите между нодовете, а именно:
са стойностите на
потока на лявата и дясната граница на нода k.
Докато непрекъснатостта на потока на границата между нода k и неговите съседи се осигурява от самото дефиниране на тези
гранични потоци, техните стойности се намират от условията за непрекъснатост на
тока на границите между нодовете, а именно: ![]() и
и ![]() . Или:
. Или: ![]() и
и ![]() . След заместване в изразите за граничните токове се получава
търсената връзка между тях и нодалните потоци:
. След заместване в изразите за граничните токове се получава
търсената връзка между тях и нодалните потоци: ![]() и
и ![]() .
.
Недостатък на получената най-проста нодална схема е, че двете допускания, на която тя се основава, а именно - заместване на производните с крайни разлики и на централните потоци със средните - са твърде груби за нодове с размер, съизмерим със стъпката на решетката от горивни касети. По тази причина реалните едроклетъчни дифузионни пресмятания се базират на по-точни, но и много по-сложни нодални схеми.
Така системата от балансни уравнение придобива стандартния
вид на система от нехомогенни линейни уравнения: ![]() , където
, където ![]() ,
, ![]() и
и ![]() . За съставяне на първото и последното уравнения, отнасящи се
за двете външни граници на реактора, се използуват съществуващите гранични
условия (напр. от логаритмичен тип). Начинът е аналогичен на вече разгледания,
а резултатът са специални изрази за коефициентите a1,1 и aN,N,
където N е броят на нодовете.
. За съставяне на първото и последното уравнения, отнасящи се
за двете външни граници на реактора, се използуват съществуващите гранични
условия (напр. от логаритмичен тип). Начинът е аналогичен на вече разгледания,
а резултатът са специални изрази за коефициентите a1,1 и aN,N,
където N е броят на нодовете.
Или, записано в матричен вид: ![]() . Ако размерите на нодовете са еднакви, то, както следва от
определенията за матричните елементи, матрицата A ще бъде симетрична. Във всички случаи тя ще бъде и диагонално
преобладаваща, което означава, че всеки неин диагонален елемент е по-голям от
сумата на модулите на извъндиагоналните елементи на съответния ред. Може да се
покаже, че реалните симетрични диагонално преобладаващи матрици са положително
определени, т.е. всички техни собствени стойности са положителни, а също така,
че собствените вектори на реалните симетрични матрици са линейно независими и
взаимно ортогонални.
. Ако размерите на нодовете са еднакви, то, както следва от
определенията за матричните елементи, матрицата A ще бъде симетрична. Във всички случаи тя ще бъде и диагонално
преобладаваща, което означава, че всеки неин диагонален елемент е по-голям от
сумата на модулите на извъндиагоналните елементи на съответния ред. Може да се
покаже, че реалните симетрични диагонално преобладаващи матрици са положително
определени, т.е. всички техни собствени стойности са положителни, а също така,
че собствените вектори на реалните симетрични матрици са линейно независими и
взаимно ортогонални.
Дву- или тримерното пространствено разбиване води до аналогични изрази за члена на утечките и до матрица със същите свойства, както в разгледания по-горе едномерен случай.
От гледна точка на решаването на получената нехомогенна линейна система са важни и следните особености на матрицата A:
- Тя е с особено голяма размерност. Така например, при едроклетъчно представяне на активната зона на ВВЕР-440 броят на уравненията може да бъде приблизително 10 000, а при финоклетъчно представяне може да достигне милион. Тъй като при стандартните преки (т.е. безитеративни) методи за решаване на нехомогенни линейни системи е нужно да се съхраняват всички матрични елементи, а необходимият брой аритметични операции за решаване на една система е от порядъка на N3, където N е броят на уравненията, прилагането на тези методи е практически невъзможно.
- Матрицата е силно разредена, т.е. има много малък брой ненулеви елементи. Както може да се види от разгледания по-горе едномерен случай, всеки неин ред освен ненулевия диагонален елемент съдържа само още два ненулеви елемента, съседни на диагоналния. Броят и разположението на ненулевите извъндиагонални елементи при дву- и тримерни задачи зависи от формата на нодовете. За реактори с квадратна решетка от касети (или елементарни клетки) едноиндексното номериране на нодовете в двумерния случай води до появата на общо четири извъндиагонални елемента, а в тримерния - до общо шест. И в двата случая матрицата е лентова, т.е. ненулевите извъндиагонални елементи са съсредоточени само в една ивица около нейния диагонал. За решаването на системи с такива матрици съществуват ефективни преки методи, изискващи брой аритметични операции, пропорционален на N. За реактори с триъгълна решетка от касети (или елементарни клетки), каквито са реакторите от типа ВВЕР, едноиндексното номериране на нодовете в двумерния случай води до появата на общо шест ненулеви извъндиагонални елемента, а в тримерния - до общо осем. За съжаление обаче, при такива решетки матрицата на системата никога не може да се представи като лентова, така че приложимите за квадратни решетки преки икономични методи за решаване на съответната линейна система са невъзможни. Във всички случаи, за решаването на системи с големи разредени матрици е целесъобразно да се прилагат методи, които изискват съхраняването само на ненулевите матрични елементи (възможно е и те изобщо да не се съхраняват, а да се пресмятат в ход на изчислителния процес). Желателно е също така броят и разположението на ненулевите елементи да не се променя е хода на изчислителния процес.
По-долу ще разгледаме накратко някои от методите, приложими за решаване на линейни системи с големи разредени матрици, нямащи лентова структура. Важна особеност на всички тях е, че те са итеративни, т.е. решението се получава чрез редица от последователни приближения.
Най-простият такъв метод е този на Якоби, или на точковата
релаксация. Итерационният процес е следният: ![]() , където j е
поредният номер на итерацията (приближението). Или, ако
, където j е
поредният номер на итерацията (приближението). Или, ако ![]() , където D съдържа
диагоналните елементи на A¸ L - поддиагоналните, U - наддиагоналните, то:
, където D съдържа
диагоналните елементи на A¸ L - поддиагоналните, U - наддиагоналните, то: ![]() . Векторът на началното приближение
. Векторът на началното приближение ![]() се избира произволно.
Нека истинското решение на системата е F,
a
се избира произволно.
Нека истинското решение на системата е F,
a ![]() е векторът на грешката
на j-тото приближение. Изваждайки
почленно уравнението
е векторът на грешката
на j-тото приближение. Изваждайки
почленно уравнението ![]() (което е в сила,
защото F е истинското решение)
от дефиниционното уравнение на итерационния процес
(което е в сила,
защото F е истинското решение)
от дефиниционното уравнение на итерационния процес ![]() , се получава:
, се получава: ![]() , или
, или ![]() . Нека li са собствените стойности на матрицата B, подредени така, че
. Нека li са собствените стойности на матрицата B, подредени така, че ![]() , a
, a ![]() са съответните им
собствени вектори. Доколкото B е
такава, че собствените й вектори образуват базис в N-мерното пространство, всеки N-компонентен
вектор, включително и
са съответните им
собствени вектори. Доколкото B е
такава, че собствените й вектори образуват базис в N-мерното пространство, всеки N-компонентен
вектор, включително и ![]() , може да се представи чрез линейна комбинация между тези
вектори:
, може да се представи чрез линейна комбинация между тези
вектори: ![]() . Тогава:
. Тогава: ![]() , ...,
, ..., ![]() . Явно е, че ако |l1| < 1, то при j ® ¥
. Явно е, че ако |l1| < 1, то при j ® ¥ ![]() ще клони към нулевия
вектор и дефинираният итерационен процес ще се схожда към истинското решение на
системата
ще клони към нулевия
вектор и дефинираният итерационен процес ще се схожда към истинското решение на
системата ![]() . Сега ще покажем, че тъй като матрицата А е диагонално преобладаваща, максималната собствена стойност на
матрицата на итерационния процес B е
по модул по-малка от единица. Нека x1,k
е максималната по модул компонента на собствения вектор x1:
. Сега ще покажем, че тъй като матрицата А е диагонално преобладаваща, максималната собствена стойност на
матрицата на итерационния процес B е
по модул по-малка от единица. Нека x1,k
е максималната по модул компонента на собствения вектор x1: ![]() . Тогава, от k-тото
уравнение на системата
. Тогава, от k-тото
уравнение на системата ![]() , а именно
, а именно ![]() следва:
следва: 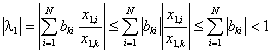 . Последното неравенство се дължи на факта, че A е диагонално преобладаваща, т.е.
. Последното неравенство се дължи на факта, че A е диагонално преобладаваща, т.е. ![]() , а
, а ![]() и
и ![]() .
.
Естествено развитие на метода на Якоби е идеята при
пресмятането на поредната компонента на новото приближение на решението да се
използуват вече получените негови компоненти, т.е. ![]() . Или, в матричен вид:
. Или, в матричен вид: 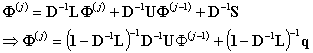 . Може да се покаже, че ако матрицата A е диагонално преобладаваща, този итерационен процес, наречен
метод на Гаус-Зайдел, или последователна релаксация, се схожда
по-бързо от метода на Якоби.
. Може да се покаже, че ако матрицата A е диагонално преобладаваща, този итерационен процес, наречен
метод на Гаус-Зайдел, или последователна релаксация, се схожда
по-бързо от метода на Якоби.
По-нататъшно усъвършенствуване на метода на Гаус-Зайдел е
т.нар. последователна свръхрелаксация,
или SOR (successive over-relaxation).
При този метод се търси подходяща линейна комбинация между двете последни
приближения ![]() и
и ![]() , получени по метода на Гаус-Зайдел, която да води до
допълнително намаляване на вектора на грешката на j -тата стъпка на итерационния процес:
, получени по метода на Гаус-Зайдел, която да води до
допълнително намаляване на вектора на грешката на j -тата стъпка на итерационния процес: ![]() . Може да се покаже, че максимално намаляване на грешката,
т.е. максимално ускоряване на сходимостта, се получава при
. Може да се покаже, че максимално намаляване на грешката,
т.е. максимално ускоряване на сходимостта, се получава при ![]() , където l1 е максималната собствена стойност на
матрицата B на метода на Якоби. На
практика множителят w
често се избира емпирично и е напр. в интервала 1.3 - 1.6.
, където l1 е максималната собствена стойност на
матрицата B на метода на Якоби. На
практика множителят w
често се избира емпирично и е напр. в интервала 1.3 - 1.6.
Друг тип итерационни схеми са от вида: ![]() . Както беше показано, такава итерационна схема ще бъде
сходяща точно тогава, когато всички собствени стойности на B са по модул по-малки от 1. Изборът на засега произволната матрица
C се прави така, че максималната по
модул собствена стойност на B да
бъде минимална, тъй като е явно, че тогава ще се постигне максимална скорост на
сходимост (на намаляване на вектора на грешката).
. Както беше показано, такава итерационна схема ще бъде
сходяща точно тогава, когато всички собствени стойности на B са по модул по-малки от 1. Изборът на засега произволната матрица
C се прави така, че максималната по
модул собствена стойност на B да
бъде минимална, тъй като е явно, че тогава ще се постигне максимална скорост на
сходимост (на намаляване на вектора на грешката).
Най-простият избор на C,
а именно ![]() , където a е подлежащ на определяне параметър, води до т.нар. оптимален едностъпков итерационен процес:
, където a е подлежащ на определяне параметър, води до т.нар. оптимален едностъпков итерационен процес:
![]() . Ако li, i = 1, ..., N са собствените стойности на A и тази матрица е симетрична и
положително определена, то li > 0. Интервалът в който
попадат тези собствени стойности обикновено може да бъде предварително оценен:
0 < m £ li £ M. От определението за матрицата на
итерационния процес B следва, че
нейните собствени стойности ще бъдат
. Ако li, i = 1, ..., N са собствените стойности на A и тази матрица е симетрична и
положително определена, то li > 0. Интервалът в който
попадат тези собствени стойности обикновено може да бъде предварително оценен:
0 < m £ li £ M. От определението за матрицата на
итерационния процес B следва, че
нейните собствени стойности ще бъдат ![]() . Ако m1 е максималната по модул измежду тях, то
скоростта на сходимост ще бъде максимална, ако a се подбере така, че
. Ако m1 е максималната по модул измежду тях, то
скоростта на сходимост ще бъде максимална, ако a се подбере така, че ![]() . Поради огромния брой на li може да се
приеме, че те заемат непрекъснати стойности в интервала [m, M]. Тогава условието
за a
се преобразува във вида:
. Поради огромния брой на li може да се
приеме, че те заемат непрекъснати стойности в интервала [m, M]. Тогава условието
за a
се преобразува във вида: ![]() . То се изпълнява при
. То се изпълнява при ![]() , т.е.
, т.е. ![]() . Явно е, че при тази стойност на a
. Явно е, че при тази стойност на a ![]() .
.
Изборът ![]() , където
, където ![]() е подлежащ на
определяне полином от степен r-1,
води до т.нар. метод на полиномите на
Чебишев. При него итерационният процес има вида:
е подлежащ на
определяне полином от степен r-1,
води до т.нар. метод на полиномите на
Чебишев. При него итерационният процес има вида: ![]() . Ако li са собствените стойности на A, то собствените стойности на B ще бъдат
. Ако li са собствените стойности на A, то собствените стойности на B ще бъдат ![]() . Следвайки разсъжденията от предходния случай, полиномът
. Следвайки разсъжденията от предходния случай, полиномът ![]() следва да се избере
така, че
следва да се избере
така, че ![]() . Доколкото е известно, че полиномът на независимата
променлива x, чийто модул при дадена
степен r и вариране на x в интервала
. Доколкото е известно, че полиномът на независимата
променлива x, чийто модул при дадена
степен r и вариране на x в интервала ![]() остава минимален, е
полиномът на Чебишев Tr(x), то
остава минимален, е
полиномът на Чебишев Tr(x), то 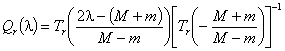 . Неговата максимална по модул стойност при вариране на l в
интервала [m, M] е
. Неговата максимална по модул стойност при вариране на l в
интервала [m, M] е 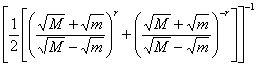 и тя е минималната
измежду всички възможности за полиноми от степен r, дефинирани в интервала [m,
M]. Както се вижда, тази стойност ще
намалява с увеличаването на r.
Практическата организация на итерациите при разглеждания метод съответствува на
r прилагания на оптималния
едностъпков итерационен процес, всеки път с различна стойност на параметъра a:
и тя е минималната
измежду всички възможности за полиноми от степен r, дефинирани в интервала [m,
M]. Както се вижда, тази стойност ще
намалява с увеличаването на r.
Практическата организация на итерациите при разглеждания метод съответствува на
r прилагания на оптималния
едностъпков итерационен процес, всеки път с различна стойност на параметъра a: ![]() . Цикълът започва с последното приближение на решението:
. Цикълът започва с последното приближение на решението: ![]() , а полученото ново приближение е
, а полученото ново приближение е ![]() . По изчислителни причини стойността на r се избира относително малка, напр. 3. Сравнявайки с
първоначалната формулировка на този метод се вижда, че
. По изчислителни причини стойността на r се избира относително малка, напр. 3. Сравнявайки с
първоначалната формулировка на този метод се вижда, че ![]() . Следователно, ai трябва да са реципрочни на нулите на Qr(l),
т.е. на нулите на
. Следователно, ai трябва да са реципрочни на нулите на Qr(l),
т.е. на нулите на ![]() , които са
, които са ![]() .
.
Всички разгледани дотук методи се характеризират с монотонно
намаляване на модула на вектора на грешката в хода на итерациите, т.е. редицата
от последователните приближения ![]() се схожда монотонно
към точното решение на линейната система
се схожда монотонно
към точното решение на линейната система ![]() . В този смисъл, критерият за прекратяване на итерациите ще
бъде
. В този смисъл, критерият за прекратяване на итерациите ще
бъде ![]() , където
, където ![]() е някаква векторна
норма, а e
е подходящо избрано малко число. На практика е удобно да се използува следният
критерий за сходимост:
е някаква векторна
норма, а e
е подходящо избрано малко число. На практика е удобно да се използува следният
критерий за сходимост: ![]() . Така се избягват допълнителни итерации заради малки и
маловажни бавно схождащи компоненти на вектора на решението.
. Така се избягват допълнителни итерации заради малки и
маловажни бавно схождащи компоненти на вектора на решението.
Измежду разгледаните методи за итеративно решаване на нехомогенни линейни системи с големи разредени матрици на практика се използуват само методът на полиномите на Чебишев и, може би, SOR. Съществуват, разбира се и други подходящи за целта методи, оставащи извън кръга на това изложение. В терминологията на реакторните пресмятания е прието този етап, на който се решава едногруповата гранична задача (в дифузионно или друго приближение) при фиксиран източник, да се нарича вътрешни итерации.
Връщайки се към въпроса за източника, който дотук беше приет
за оценен на базата на предходно приближение за потока и за коефициента на
размножение, общият матричен запис на пространствено дискретизираното
многогрупово условно-критично дифузионно уравнение ще бъде ![]() . Векторът
. Векторът ![]() е обединение на
векторите Fg, въведени
по-горе като решения на едногруповите нехомогенни уравнения; матрицата A има блочна структура, съставена от
матриците Ag на тези
уравнения; матрицата F е
пространствено и енергетично изображение на източника на неутрони от делене
е обединение на
векторите Fg, въведени
по-горе като решения на едногруповите нехомогенни уравнения; матрицата A има блочна структура, съставена от
матриците Ag на тези
уравнения; матрицата F е
пространствено и енергетично изображение на източника на неутрони от делене ![]() ; а, както беше показано в Глава 3, l трябва да има смисъл на
ефективен коефициент на размножение. Многогруповото условно-критично дифузионно
уравнение може да се запише във вида на стандартна собствена задача:
; а, както беше показано в Глава 3, l трябва да има смисъл на
ефективен коефициент на размножение. Многогруповото условно-критично дифузионно
уравнение може да се запише във вида на стандартна собствена задача: ![]() . Съгласно разглежданията в Глава 3, именно максималната
собствена стойност на B, т.е. l1,
има смисъл на ефективен коефициент на размножение keff на реактора, а съответният й собствен вектор - на
скаларния неутронен поток в този реактор. По-долу ще покажем, че въведеното
разделяне на решаването на многогруповото условно-критично уравнение на два
етапа, първият от които са вече разгледаните вътрешни итерации, ще доведе по
естествен път до решаване и на дефинираната тук собствена задача.
. Съгласно разглежданията в Глава 3, именно максималната
собствена стойност на B, т.е. l1,
има смисъл на ефективен коефициент на размножение keff на реактора, а съответният й собствен вектор - на
скаларния неутронен поток в този реактор. По-долу ще покажем, че въведеното
разделяне на решаването на многогруповото условно-критично уравнение на два
етапа, първият от които са вече разгледаните вътрешни итерации, ще доведе по
естествен път до решаване и на дефинираната тук собствена задача.
Нека ![]() е произволен ненулев
вектор и организираме следната итерационна процедура:
е произволен ненулев
вектор и организираме следната итерационна процедура: ![]() . Нека собствените стойности на матрицата B са
. Нека собствените стойности на матрицата B са ![]() , a
, a ![]() са съответните им
собствени вектори. Приемайки, че тези вектори образуват базис в N-мерното пространство (където N е размерността на B), винаги е възможно да се въведе представянето:
са съответните им
собствени вектори. Приемайки, че тези вектори образуват базис в N-мерното пространство (където N е размерността на B), винаги е възможно да се въведе представянето: ![]() . Тогава,
. Тогава, ![]() . Или, записано за k-тата
компонента на
. Или, записано за k-тата
компонента на ![]() :
: ![]() . Следователно:
. Следователно: 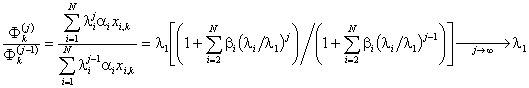 , където
, където ![]() . Тъй като k е
избрано произволно, критерий за достигане на сходимост може да бъде
сближаването на отношенията
. Тъй като k е
избрано произволно, критерий за достигане на сходимост може да бъде
сближаването на отношенията ![]() при различни k. Приближение за собствения вектор x1, съответствуващ на
максималната собствена стойност l1, очевидно ще бъде
при различни k. Приближение за собствения вектор x1, съответствуващ на
максималната собствена стойност l1, очевидно ще бъде ![]() . Множителят
. Множителят ![]() е формално без
значение, защото както собствените вектори на една матрица, така и неутронният
поток в условно-критичния реактор са определени с точност до произволен ненулев
множител. Описаната итерационна процедура се нарича степенен метод, или степенна
итерация. Ако собствените вектори xi
са взаимно ортогонални (какъвто е на практика случаят при матрицата B, породена от многогруповата
дифузионна условно-критична задача), то
е формално без
значение, защото както собствените вектори на една матрица, така и неутронният
поток в условно-критичния реактор са определени с точност до произволен ненулев
множител. Описаната итерационна процедура се нарича степенен метод, или степенна
итерация. Ако собствените вектори xi
са взаимно ортогонални (какъвто е на практика случаят при матрицата B, породена от многогруповата
дифузионна условно-критична задача), то ![]() , където bi са множители, чиито конкретни стойности
нямат значение. Тогава максималната собствена стойност може да се оцени от
отношението
, където bi са множители, чиито конкретни стойности
нямат значение. Тогава максималната собствена стойност може да се оцени от
отношението ![]() , където
, където ![]() е евклидовата векторна
норма. Явно е, че редицата от оценки
е евклидовата векторна
норма. Явно е, че редицата от оценки ![]() ще се схожда монотонно
към истинската максимална собствена стойност l1, така че
критерий за прекратяване на итерациите може да бъде
ще се схожда монотонно
към истинската максимална собствена стойност l1, така че
критерий за прекратяване на итерациите може да бъде ![]() , където e е подходящо избрано малко число. Връщайки се към
множителя
, където e е подходящо избрано малко число. Връщайки се към
множителя ![]() , съдържащ се в текущото приближение на потока
, съдържащ се в текущото приближение на потока ![]() , се вижда, че ако коефициентът на размножение се отличава
съществено от 1, то при достатъчно голям номер на итерацията j има опасност компонентите на
, се вижда, че ако коефициентът на размножение се отличава
съществено от 1, то при достатъчно голям номер на итерацията j има опасност компонентите на ![]() да станат прекалено
големи или малки и да настъпят изчислителни проблеми. Тъй като нормирането на
потока между две последователни итерации не влиза в противоречие с направените
дотук изводи за метода на степенната итерация, е целесъобразно всеки път да се
прави нормировката
да станат прекалено
големи или малки и да настъпят изчислителни проблеми. Тъй като нормирането на
потока между две последователни итерации не влиза в противоречие с направените
дотук изводи за метода на степенната итерация, е целесъобразно всеки път да се
прави нормировката ![]() . Тогава текущата оценка на l1 ще бъде
. Тогава текущата оценка на l1 ще бъде ![]() , където
, където ![]() е все още ненормиран и
е използуван фактът, че
е все още ненормиран и
е използуван фактът, че ![]() . Така нормировката на потока може да се запише като:
. Така нормировката на потока може да се запише като: ![]() . Отчитайки последното, както и определението за матрицата B, степенната итерация ще има вида:
. Отчитайки последното, както и определението за матрицата B, степенната итерация ще има вида: ![]() . Това е всъщност съвместен еквивалентен запис на решенията
на груповите нехомогенни дифузионни уравнения с източник, оценен от предходните
приближения на keff и
груповите потоци:
. Това е всъщност съвместен еквивалентен запис на решенията
на груповите нехомогенни дифузионни уравнения с източник, оценен от предходните
приближения на keff и
груповите потоци: ![]() .
.
На основата на казаното дотук следва, че описаната
итерационна процедура ще се схожда към истинския скаларен поток и коефициент на
размножение в условно-критичния реактор (естествено, в рамките на въведената
пространствена и енергетична дискретизация). В терминологията на реакторните
пресмятания тя се нарича итерации по
източника, или външни итерации.
Тук е уместно да се отбележи, че функцията на вътрешните итерации се свежда
единствено до обръщането на матриците Ag,
и ако то се прави явно или неявно по безитеративен начин, такива няма да има.
Съществуват различни методи за ускоряване на външните итерации, чието
разглеждане обаче ще остане извън кръга на това изложение. Тук може само да се
спомене, че тези методи като правило се базират на оценяване на отношението ![]() (наричано доминантно отношение), тъй като от
изложеното по-горе следва, че именно то определя главната компонента на
грешката на задачата за намиране на максимална собствена стойност и съответния
й собствен вектор.
(наричано доминантно отношение), тъй като от
изложеното по-горе следва, че именно то определя главната компонента на
грешката на задачата за намиране на максимална собствена стойност и съответния
й собствен вектор.
Над външните итерации се организират итерации за търсене на критичност, свеждащи се до вариране на материалния състав на реакторната среда (напр. борна концентрация и/или позиция на ОР СУЗ) с цел постигане на keff = 1, а над итерациите за търсене на критичност - итерации по изгарянето. При последните задачата е да се пресметне изменението на дълбочината на изгаряне за определен интервал от горивната кампания. Тя се решава итеративно, защото материалните свойства на средата, респ. матриците A и F, зависят от търсената дълбочина на изгаряне. В хода на тези итерации се пресмята и отравянето (образуване, разпадане и изгаряне на продукти на деленето с големи сечения за поглъщане на неутрони).
Програмните продукти, използувани за експлоатационни пресмятания на неутронно-физичните характеристики са реализации на изчислителни схеми, които следват очертаните по-горе общи принципи. При тях броят на енергетичните групи е сведен до две - топлинна и надтоплинна, а основна предпоставка за точност на решението са специално конструираните нодални схеми. Необходимите за работата на тези програмни продукти библиотеки от групови дифузионни константи са предварително подготвени и представляват неделима част от изчислителния комплекс. Примери са такива комплекси, използувани за реакторите ВВЕР-440 и ВВЕР-1000 в АЕЦ “Козлодуй”, са БИПР-7 (ИЯР РНЦ "Курчатовский институт") и SPPS-1.6 (ИЯИЯЕ-БАН).