10. Непрекъснати разпределения

 

 

       10.1. Равномерно разпределение

  10.2. Нормално разпределение

 10.2.1. Лапласов модел на грешките

 10.2.2. Свойства на нормалното разпределение

 10.2.3. Нормалното разпределение и грешките при експеримента: модел на Хершел (J.Hershel)

   10.3. Разпределение

 

10.1. Равномерно разпределение

Това е най-простият пример за непрекъснато разпределение. Едно статистическо разпределение се нарича равномерно разпределение, ако вероятностната му плътност е константа в някакъв краен интервал и нула извън него:

                                                                                (1)

Нормировка:

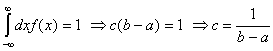                                                       (2)

Функция на разпределение:

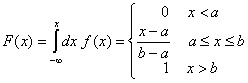                                                             (3)

Математическо очакване:

                                                                           (4)

Дисперсия:

                                                                                           (5)

f(x)                                                             F(x)

 

 

           a         b            x                                a        b         x

 

Равномерното разпределение само по себе си е от неголямо значение за практически приложения. То обаче е много удобно за пресмятания и играе важна роля при трансформациите на статистическите разпределения (например при моделирането със случайни числа).

10.2. Нормално разпределение

10.2.1. Лапласов модел на грешките

В произведението си "Философско есе върху теорията на вероятностите" през 1783г. Лаплас (P.Laplace) е разгледал въпроса за произхода на грешките в наблюденията. Той е предполагал, че:

·        истинската стойност на измеряемата величина съществува обективно и има някаква точна и постоянна стойност, равна на някаква константа ;

·         не може да се измери точно, тъй като резултатите от измерването се изкривяват от голям брой () независими помежду си смущения, всяко от които е с големина;

·        всяко едно от смущенията с равна вероятност води до отклоняване на стойността на наблюдаемата величина на ;

·        грешката на измерването се образува от сумирането на влиянието на отделните смущения.

 

Ясно е, че в този модел вероятностното разпределение на резултатите от измерванията се описва с биномно разпределение. Развитието на влиянието на грешките върху стойността на резултатите от наблюденията изглежда по следния начин:

 

 

В таблицата е дадена вероятността да се получи даден резултат от измерването след въздействието на определен брой смущения. В началната точка отсъствуват смущения и затова с вероятност 1 ние получаваме истинската стойност на измеряемата величина . С появата на едно смущение с равна вероятност (1/2) се получава резултат  или . Същото става и при всяко следващо смущение, т.е. всеки ред се получава от предишния чрез сумиране на ефекта от предишните смущения и последното по схемата на Лаплас. Това е впрочем вероятността за .

Сега, по-интересно е да видим какво става при неограничено нарастване на броя на смущенията: . Макар че в оригиналния модел на Лаплас , то резултатът, който следва, е валиден и за  (т.е. за асиметрия в посоките на отклонение на резултата под действието на смущението).

Този резултат (известен като локална теорема на Моавр-Лаплас (Moivre-Laplace), която няма да доказваме) гласи, че за всички нормирани бернулиеви случайни величини  от вида:

                                                                                                         (1)

където  е някое цяло число, при е в сила:

                                                                                 (2)

По-общо, разпределението (2) има вероятностна плътност от вида:

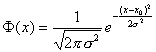                                                                                    (3)

Математическото очакване на случайната величина с вероятностна плътност (3) е:

                                                                                                          (4)

а дисперсията й е:

                                                                                                        (5)

Това разпределение се нарича нормално, или Гаусово. То заема централно място в математическата статистика и по-специално в теорията на грешките. Разпределението, описвано с вероятностната плътност (2), се нарича стандартно нормално разпределение. То има средна стойност нула и дисперсия 1.

10.2.2. Свойства на нормалното разпределение

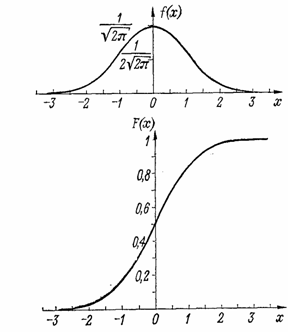
Вероятностната плътност на нормалното разпределение (3) представлява  камбановидна крива, симетрична спрямо точката . Tя има инфлексни точки при стойности на аргумента , където втората производна става нула и наклонът на кривата се сменя. Това разпределение зависи от два параметъра - средната стойност  и дисперсията . Използува се и означението:

                                                                                             (6)

Функцията на разпределение на стандартното нормално разпределение е:

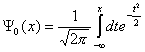                                                                                       (7)

Тази функция е свързана с известната специална функция :

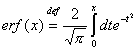                                                                                         (8)

Именно:

Функцията (7) се нарича интеграл на вероятностите.

Вероятността една нормално разпределена случайна величина да се отличава от средната си стойност с по-малко от е:

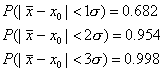                                                                                              (9)

От тези съотношения се вижда, че нормално разпределената случайна величина е групирана в близка околност на средната си стойност (с радиус от порядъка на s). По-нататък ще видим, че в много случаи в добро приближение може да се счита, че неопределеностите (грешките) при измерванията са разпределени нормално около средната стойност . В такъв случай стандартното отклонение  може да бъде разглеждано като мярка за големината на случайните грешки при измерванията.

Едно друго важно свойство на нормалното разпределение е, че сумата на две независими случайни величини с Гаусови разпределения е също нормално разпределена със средна стойност  и с дисперсия . Това свойство обаче е само частен случай от един много по-общ резултат, известен като централна гранична теорема. Самата централна гранична теорема (ЦГТ) има различни формулировки с различна степен на общност. Може да се установи например, че ако е множество от независими случайни величини, еднакво разпределени със средни стойности и дисперсии , то сумата при се подчинява на Гаусово разпределение с параметри . Забележете, че в тази формулировка никъде не става дума за конкретния вид на вероятностното разпределение на всяка от величините (т.е. тяхното разпределение може да е произволно; достатъчно е само средните стойности и дисперсиите да са еднакви, и теоремата пак ще е вярна!). Може да се покаже, че сумите от случайни величини се подчиняват на нормално разпределение дори и при по-слаби предположения от тези, в частност когато не всичките имат еднакви разпределения. Ние няма да се занимаваме с най-общата формулировка на ЦГТ, но е важно да знаем, че нормалното разпределение е добро приближение за статистическото разпределение на измерваните величини в много широк клас случаи.

10.2.3. Нормалното разпределение и грешките при експеримента: модел на Хершел (J.Hershel)

С помощта на ЦГТ Лапласовият модел за грешките може да бъде изтълкуван като модел за сумарното въздействие на малки индивидуални ефекти върху резултата от измерването. Първоначалното предположение за еднакви амплитуди на всичките смущения сега може да се отхвърли и въпреки това се получава нормално разпределение на грешките в резултата (вж. предишния раздел). В стремежа да се изяснят границите на приложимост на нормалното разпределение като модел за описание на грешките при измерванията е интересно да се разгледа модела на астронома Хершел, който е извел нормалното разпределение при много слаби предположения.

Хершел разглежда падането от точка  върху една равнина на малки топчета. Поради случайни смущения не всички топчета падат върху една и съща точка от равнината. Ние се интересуваме при това от вероятностната плътност на разпределение на координатите на топчетата, т.е. от вероятността за попадане на едно топче върху елементарната площ . Този елемент може да се разглежда както в декартови, така и в полярни координати. Предполагаме, че са взети мерки да няма систематични отклонения от центъра; тогава всички ъгли на отклонение са равновероятни (т.е. имаме ъглова симетрия). В такъв случай вероятностната плътност в полярни координати ще зависи само от радиус-вектора. Ние я означаваме с .

Предполагаме още, че попадането на топчето в интервала е независимо от попадането му в интервала . Поради вече предположената ъглова симетрия, вероятностната плътност по  и по  ще има еднакъв вид, т.е. ще е в сила:

                                                                                           (1)

Или, вероятността за попадане в елементарната площ  ще бъде:

                                                                                    (2)

Логаритмуваме двете страни:

                                                                                (3)

Преминавайки и в дясната страна на (3) към полярни координати, имаме:

                                                                 (4)

Сега диференцираме двете страни спрямо полярния ъгъл :

                                                        (5)

Връщайки се отново в декартови координати, получаваме:

                                                                                      (6)

Прегрупираме и стигаме до израза:

                                                                                                  (7)

Поради независимостта на  и  това функционално равенство може да бъде изпълнено за всяко ,  само ако всяка от двете му страни поотделно е равна на константа:

                                                                                                         (8)

Следователно:

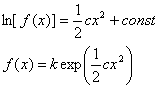                                                                                    (9)

Тъй като вероятността трябва да е ограничена при , то очевидно трябва да е изпълнено: . Означаваме: . Тогава получаваме последователно:

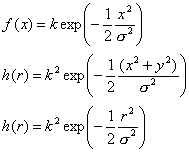                                                                            (10)

Какво се оказа? При много общи и много естествени предположения за независимост и симетрия ние  получихме нормално разпределение за отклоненията. Това е демонстрация на правдоподобността при използуване на Гаусовото разпределение като модел на грешките при измерванията. Това заключение е от решаваща важност в много случаи, особено в теорията на метода на най-малките квадрати.

Въпреки това ние трябва да помним, че нормалното разпределение не е природен закон. Причините за появата на неопределености при измерванията са твърде многообразни, за да могат да се обхванат с една формула всевъзможните им проявления. Симетрията и независимостта, макар и да са много общи качества, не винаги са изпълнени в конкретните експерименти. Затова трябва да се проверява нормалността на разпределението на отклоненията винаги, когато това е възможно, още преди да са извършени (понякога твърде обширните) пресмятания, които са валидни обаче само за случая на Гаусово разпределение.

10.3. Разпределение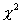

Тук ще дадем кратки сведения (без доказателства) за още едно важно непрекъснато разпределение.

Нека  са независими случайни величини, които имат стандартно нормално разпределение . Тогава сумата:

                                                                                                           (1)

е случайна величина, чиято вероятностна плътност има вида:

                                                                                      (2)

където:

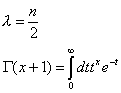                                                                                             (3)

 е гама-функцията на Ойлер (L.Euler). Числото , което е единственият параметър на разпределението (2), се нарича брой на степените на свобода. Разпределението (2) се нарича разпределение хи-квадрат ().

Едно важно свойство на разпределението  е следното:

сумата на две независими случайни величини с разпределения  съответно с n₁ и n₂ степени на свобода се подчинява на разпределение  с n₁+n₂ степени на свобода. 

Математическото очакване и дисперсията на  разпределението с плътност (2) са съответно:

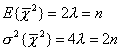                                                                                             (4)

 

 

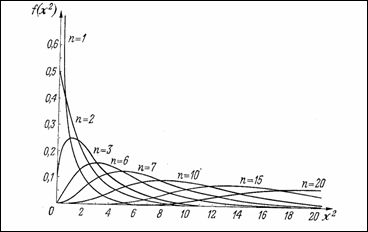
На фигурата е показана вероятностната плътност на разпределението  за различен брой степени на свобода. Вижда се, че с увеличаването на   разпределението става все по-симетрично (и все по-широко).

Разпределението  намира приложение поне в два много важни случая:

·        при проверката на хипотезата за вероятностната плътност на случайна величина, измерена в някакъв експеримент ( критерий за съгласие);

·        при проверката на резултатите от оценките по метода на най-малките квадрати.

Ако величинитe  имат разпределение не , a , то величината:

                                                                                            (5)

се подчинява на разпределение с  степени на свобода.