11. Извадки

 

   11.1. Случаен избор. Разпределение на извадките

   11.2. Оценки на параметри. Свойства на оценките

   11.3. Оценки за средната стойност и дисперсията на вероятностното разпределение

 

11.1. Случаен избор. Разпределение на извадките

Извадката се прави измежду множество елементи. Размерът на това множество е обикновено безкраен. То всъщност се състои от всевъзможните изходи от експериментите от даден вид. Такова множество се нарича популация (често се използува и терминът генерална съвкупност).

Ако е осъществена извадка от  елемента, казва се, че извадката е с обем .  Важно е да се знае, че обемът на извадката е винаги краен.

Нека разпределението на случайната величина   в популацията се описва с вероятностната плътност . Ние се интересуваме от стойностите на , които се съдържат в елементите на извадката. Предполагаме, че сме извършили последователно  извадки с обем за всяка от тях  и при това сме получили следните резултати:

                                                                                                        (1)

Резултатът от всяка извадка може да бъде групиран в една -мерна случайна величина:

                                                                                            (2)

която може да се разглежда като вектор в пространството на -мерните извадки (напомняме, че случайната величина , която всъщност изучаваме и чиито всевъзможни реализации образуват популацията, е само една). Тази случайна величина има вероятностна плътност:

                                                                                       (3)

Ние казваме, че плътността  описва процеса на случаен избор тогава и само тогава, когато са изпълнени следните условия:

·        случайните величини  са независими, т.е.:

;                                                                     (4)

·        всяка вероятностна плътност в (4) е равна на вероятностната плътност на случайната величина  в популацията:

                                                             (5)

Ако не е уговорено друго, по-нататък ще считаме, че извадките, които разглеждаме, са резултат именно от случаен избор.

Трябва да се отбележи, че в реалния процес на избор е много трудно да се осъществи неговата случайност, а пък още по-трудно е да се убедим, че сме я постигнали. Това означава да премахнем систематичните отклонения в процеса на измерване и да оставим да действуват само случайни фактори (и то едни и същи в целия процес на получаване на извадката). На по-обичаен език това означава да осигурим условия за повторяемост на резултатите от експеримента.  Това е едно от главните умения на добрия експериментатор.

Сега да предположим, че все пак сме осигурили условията за случаен избор. Нека елементите на извадката да са подредени в редица по възходящите стойности на  (съгласно правилата на случайния избор това не е ограничение на общността на разглеждане), и нека  е броят на елементите, за които . Тогава функцията:

                                                                                                    (6)

може да се разглежда като емпирична функция на вероятностно разпределение на случайната величина . Тази функция е стъпаловидна и тя нараства с  всеки път, когато стане равно на някоя от стойностите на така подредените елементи на извадката. Тази функция (6) се нарича разпределение на извадката. Очевидно,  е приближение на функцията на разпределение на популацията , към която се стреми при неограничено нарастване на .

Всяка функция на елементите на извадката (2) е случайна величина. Такива случайни величини се наричат статистики. Най-известният пример за статистика е средното аритметично на извадката:

                                                                                    (7)

11.2. Оценки на параметри. Свойства на оценките

Една типична задача на анализа на данни е следната: Предполагаме, че е известен общият вид на вероятностната плътност на (разпределението на) популацията. От експеримента е получена една извадка, от която трябва да се получи числовата стойност на един (или повече) параметър/ри. Поради крайния обем на извадката резултатът не може да бъде точен. Така възниква задачата за оценка на параметри.

Тъй като оценяваната стойност на параметъра се получава с помощта на извадката, то очевидно това е някаква статистика от специфичен вид; такава статистика се нарича оценка: . Казва се още, че статистиката  служи за оценка на параметъра  или пък че  e oценка за .

Една оценка се нарича неотместена, ако за извадка с произволен обем нейното математическо очакване е равно на оценявания параметър:

                                                                                 (8)

Една оценка се нарича състоятелна, ако тя се схожда по вероятност към стойността на оценявания параметър (т.е. при неограничено нарастване на обема на извадката точността на оценката също неограничено нараства). Или, за състоятелните оценки е в сила:

                                                                                                      (9)

Накрая, не всички оценки са еднакво ефективни. За сравняване на ефективността на две оценки за един и същ параметър може да се използува съотношението:

                                                                                                       (10)

По-ефективната оценка има при един и същ обем на извадката по-малка дисперсия. По-нататък ще видим, че понякога е възможно да се установи точна долна граница на дисперсията за всевъзможните оценки на даден параметър. Естествено, ако съществува оценка, за която се достига тази долна граница на дисперсията, то тя е за предпочитане пред останалите, тъй като е по-ефективна от всички тях.

11.3. Оценки за средната стойност и дисперсията на вероятностното разпределение

Средната стойност и дисперсията на вероятностното разпределение на популацията са най-често оценяваните параметри при физичните експерименти. Ето защо ние искаме да построим подходящи статистики, които да се използуват за оценки на тези параметри.

Разглеждаме извадка с обем , получена чрез случаен избор от дадена популация на случайната величина , описваща се с вероятностна плътност . Ще установим, че средното аритметично на извадката:

                                                                                               (1)

е неотместена и състоятелна оценка за средното на популацията.

Тъй като  всъщност е функция на случайни величини, то самото е също случайна величина. Тя е статистика, тъй като е функция на елементите на извадката. Нейното математическо очакване е:

                                                                          (2)

т.е. то е равно на математическото очакване на популацията (и то за всяко ); следователно, (1) представлява неотместена оценка за средното на популацията.

За да установим, че статистиката (1) е и състоятелна оценка, ние пресмятаме нейната дисперсия:

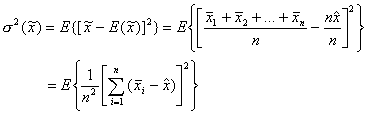                                (3)

Тъй като компонентите на извадката  са взаимно независими (по определение това е случаен избор), то смесените членове в сумата от вида са всичките нули при (това са всъщност ковариациите). Оттук получаваме:

                                                                         (4)

Тук  е кой да е елемент от извадката (те всичките имат еднакво разпределение и следователно, равни дисперсии). От (4) се вижда, че , с което се установява състоятелността на оценката (1) за математическото очакване на популацията . Ще отбележим още, че стойността на всяко отделно измерване (т.е. всяка случайно избрана стойност ) е също така неотместена оценка за . Тя обаче не е състоятелна.

Сега да потърсим оценка за дисперсията на популацията. Определяме (засега) дисперсията на извадката като средно аритметично на средноквадратичните отклонения от средното на извадката:

                                                                                           (5)

Сега ние искаме да проверим дали тя е неотместена и състоятелна оценка за дисперсията на самата популация.

Пресмятаме първо математическото очакване на тази оценка:

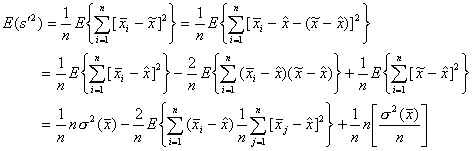     (6)

Тези преобразования се правят по аналогия с извършеното в предишната точка. Във втория член остават ненулеви само диагоналните членове , тъй като отново недиагоналните са нули (ковариации на независими поради правилата на случайния избор величини).

Окончателно:

                                              (7)

Вижда се, че , т.е. оценката (5) не е неотместена оценка за дисперсията на популацията (нейното отместване впрочем клони към нула при ; такива оценки се наричат асимптотично неотместени). Същевременно става ясно, че следната оценка:

                                                                                       (8)

е неотместена оценка за дисперсията на популацията.

Може да се установи (по аналогичен начин), че (8) е и състоятелна оценка за дисперсията на популацията.

Множителят в дефиницията (8) изглежда донякъде странен. За да се установи неговият смисъл, си представяме, че . Тогава средното аритметично на извадката е равно на стойността на единствения й елемент, и според първоначалната дефиниция за дисперсията (5) тя би станала 0 (т.е. безкрайно точно измерване?), което очевидно не може да е вярно. Според неотместената оценка (8) в случая на извадка с обем единица дисперсията на популацията остава неопределена (), т.е. тя не може да бъде оценена. Причината е, че информацията, съдържаща се в стойността на измерването вече е използувана за оценка на - средната стойност на разпределението на популацията.

Друга гледна точка за обяснението на този множител е, че при определянето на оценката (5), респ. (8), елементите не са вече всичките независими – между тях се е появила една връзка с определянето на средното им аритметично чрез (1). По такъв начин, ефективният брой на елементите в извадката се намалява с един. В такъв случай се казва, че броят на степените на свобода на оценката  е равен на .

Оценката (1) се нарича още емпирично средно, а (8) – емпирична дисперсия на извадката. Положителният квадратен корен от (8) се нарича емпирично средноквадратично отклонение (за извадката).

Може да се установи, че всяко допълнително уравнение (връзка) между - елементите на извадката, намалява броя на степените й на свобода с единица. Ние ще използуваме този резултат по-нататък без доказателство.