12. Функция на правдоподобие

Досега ние разглеждахме въпроса за оценка на параметри. Бяха посочени някои желателни свойства на оценките, но без да се каже как да се построят оценки с такива свойства в конкретните случаи. Оценки бяха получени само за такива (наистина много важни) величини като математическото очакване и дисперсията, но техният вид като че ли пада от небето. Сега ние ще разгледаме една по-обща задача:

Нека разглеждаме една -мерна случайна величина: ;  са нейните компоненти,  на брой, които са също така случайни величини. Популацията в този случай се състои от всевъзможните експерименти, при които се получава някаква конкретна, фиксирана стойност на . (Например,  може да е цял спектър, т.е. последователност от еквидистантни измервания, при което  е номерът на съответния канал, а  са случайни величини, описващи резултатите от измерванията в съответните канали).

Предполагаме още, че съвместното вероятностно разпределение на величините  напълно се определя от параметрите ,  на брой. Вероятностната плътност на разпределение на случайната величина  се записва така: .

Нека сме извършили единичен експеримент, подчиняващ се на правилата за случаен избор (все едно, сме измерили един спектър, но с  компоненти). На този експеримент може да се съпостави едно число:

                                                                                          (1)

Числото  показва - след като резултатът от експеримента е вече известен - с каква вероятност този резултат е могъл да бъде очакван. То има характер на апостериорна вероятност. За извадка с обем  (независими елементи), тази вероятност се определя като произведение:

                                                                                        (2)

при това  е функция на параметрите . Съществуват ситуации, в които е известно, че популацията може да се опише с един от два възможни и различни набора от параметри  и  . Образуваме отношението:

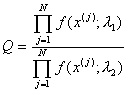                                                                                            (3)

Резултатът от един конкретен (случаен) избор (измерване) може да се изрази така: наборът от параметри  е  пъти по-вероятен от набора . Изразът (3) се нарича отношение на правдоподобие, а функцията:

                                                                                                          (4)

се нарича функция на правдоподобие.

Много важно е да се разбере разликата между така определената функция  и обикновената (априорна) вероятност. Именно, при априорната вероятност (apriori = преди експеримента) ние предполагаме, че имаме някакви зададени, фиксирани стойности на параметрите  и като знаем вероятностната плътност , ние можем да определим (да предскажем) вероятността да се получи някакъв резултат (например, че ), т.е. тогава l са параметри, а  - аргументи. При апостериорната вероятност резултатите от измерването са вече известни (това са векторите , които са фиксирани), и ние можем по тези резултати от експеримента да оценяваме величините l, които са сега аргумент на функцията на правдоподобие  (а фиксираните в този случай са, напротив, параметри).

Разглеждайки конструкцията на понятието отношение на правдоподобие, лесно може да се стигне до заключението, че най-голямо доверие заслужават онези стойности на параметрите l, при които се реализира максимум на функцията на правдоподобие . В това собствено се състои и принципът на максималното правдоподобие (англ. maximum likelyhood principle).

На фигурата са показани някои най-характерни възможни профили на функцията на правдоподобие (за един параметър).

 

 

 

 

L(l)

 

                  l^*        l        l^*              l         l₁^*        l₂^*    l₃^*   l

 

В първия случай ние сме в най-благоприятна ситуация (функцията на правдоподобие е симетрична камбановидна крива). Несъмнено, стойността , съответствуваща на максимума на , може да се приеме като най-добра оценка на параметъра l. Функцията на правдоподобие задава едно разпределение (тя е пропорционална на вероятностната плътност при съответната нормировка), чиято дисперсия е мярка за неопределеността на оценката за параметъра l.

Във втория случай (на унимодално асиметрично разпределение) най-вероятната стойност  все още е най-добра оценка за параметъра l. Дисперсията обаче, въпреки че запазва своя математически смисъл, не е вече така удовлетворителна оценка за описание на поведението на функцията около нейния максимум. В този случай е по-добре заедно с  да се пресмятат и по-висшите моменти или дори цялата съвместна вероятностна плътност .

Може накрая да се случи и така, че  да има няколко локални максимума. В този случай обикновено се отдава предпочитание на най-големия максимум на функцията на правдоподобие. Но пресмятанията, свързани с намирането на глобалния максимум, могат да бъдат много сложни (и продължителни), особено при многопараметрични задачи. Вероятността за появата на множество локални максимуми на  корелира с възможността за получаване на нееднозначно решение на физическата задача, от която всъщност сме тръгнали. Това може да се случи най-често при:

·        малък брой наблюдения;

·        лоша статистическа точност на измерванията;

·        недобре определени начални предположения за вида на зависимостта , която е често само приблизително известна.

В такива случаи е необходимо, очевидно, крайно внимание при интерпретацията на резултатите.