16. F-критерий за равенство на дисперсиите
Проблемът за
сравняване на дисперсии възниква обикновено във връзка с повторни измервания на
една и съща случайна величина, да речем с различни прибори или по различни
методики. Друг пример е влошаването на точността на показанията на някакъв
прибор с течение на времето поради различни причини. Може да възникне въпросът
дали това се е случило. Това би могло да се установи, ако имаме две серии
(извадки) от измервания, правени с този прибор в различни моменти от време на
едни и същи еталонни образци. Тогава средните стойности са равни (ако няма
систематични грешки), но дисперсиите са, изобщо казано, различни.
И така, предполагаме,
че имаме две извадки от съвкупности с нормално разпределение, с обеми съответно
![]() и
и ![]() . Нулевата хипотеза е: дисперсията
на двете серии измервания е еднаква.
. Нулевата хипотеза е: дисперсията
на двете серии измервания е еднаква.
Статистиката,
въз основа на която се строи критерият, се избира така:
![]() (1)
(1)
където ![]() и
и ![]() са емпиричните дисперсии на извадките
са емпиричните дисперсии на извадките ![]() и
и ![]() . Ясно е, че ако двете дисперсии са равни,
. Ясно е, че ако двете дисперсии са равни, ![]() ще е близко до 1.
Известно е, че ако разпределението на популацията е нормално, статистиките:
ще е близко до 1.
Известно е, че ако разпределението на популацията е нормално, статистиките:
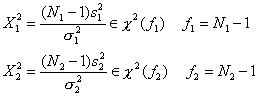 (2)
(2)
имат
разпределение ![]() със съответния брой
степени на свобода. Ако нулевата хипотеза е вярна, то
със съответния брой
степени на свобода. Ако нулевата хипотеза е вярна, то ![]() (това е всъщност
дисперсията на популацията, която в този случай е една и съща). Тогава:
(това е всъщност
дисперсията на популацията, която в този случай е една и съща). Тогава:
![]() (3)
(3)
т.е. ![]() е отношение на две
статистики с разпределение
е отношение на две
статистики с разпределение ![]() .
.
Вероятностната
плътност на разпределението ![]() е:
е:
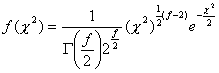 (4)
(4)
Сега ние
търсим вероятността:
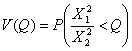 (5)
(5)
Тя ще се
получи с интегриране в триъгълната област:
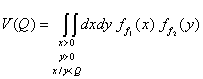 (6)
(6)
Този
интеграл води до:
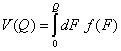 (7)
(7)
където за
вероятностната плътност ![]() имаме:
имаме:
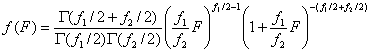 (8)
(8)
Това
разпределение се нарича разпределение
на Фишер (Fisher). То има два параметъра – двете степени на свобода ![]() и
и ![]() . То е донякъде подобно по форма на разпределението
. То е донякъде подобно по форма на разпределението ![]() - има ненулева плътност само за
- има ненулева плътност само за ![]() . При
. При ![]() математическото му
очакване е:
математическото му
очакване е: ![]() .
.
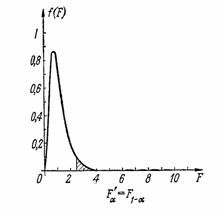
Обобщавайки,
хипотезата за равенство на дисперсиите на две извадки се проверява така:
·
избира се нивото на значимост a;
·
определяме границата на критичната
област (защрихованата на фигурата) от условието: ![]() . Ясно е, че
. Ясно е, че ![]() е квантилът на разпределението на Фишер на ниво
е квантилът на разпределението на Фишер на ниво ![]() ;
;
·
извършваме измерванията; определяме
емпиричните дисперсии ![]() и пресмятаме
и пресмятаме ![]() от (1);
от (1);
·
Ако ![]() , то ние се намираме в критичната област и нулевата хипотеза
се отхвърля за нивото на значимост a. Тогава
можем да заключим, че
, то ние се намираме в критичната област и нулевата хипотеза
се отхвърля за нивото на значимост a. Тогава
можем да заключим, че ![]() , тъй като критерият тук е едностранен.
, тъй като критерият тук е едностранен.