17. Т-критерий за сравняване на средни

 

 

17.1. Т-критерий за сравняване на средна стойност с константа

    17.2. Т-критерий за сравняване на средните на две извадки

 

17.1. Т-критерий за сравняване на средна стойност с константа

Първо ще разгледаме случая на една случайна величина с нормално разпределение. Нулевата хипотеза е, че математическото очакване на популацията е . Правим извадка с обем ; нека средното на извадката е . Дисперсията на това средно е:

                                                                                             (1)

Съгласно централната гранична теорема, за достатъчно голяма извадка средното  клони към случайна величина с нормално разпределение . Следователно, съответната нормирана случайната величина ще има стандартно нормално разпределение:

                                                                                          (2)

С това задачата би се свела до познатата задача за проверка на хипотезата за принадлежност към стандартно нормално разпределение, ако  би била известна. Проблемът е, че обикновено  не е известна; вместо нея ние разполагаме само с една нейна оценка чрез извадката:

                                                                                 (3)

Съответната оценка за ще бъде:

                                                             (4)

Сега, ние се интересуваме от разпределението на случайната величина:

                                                                                              (5)

Очевидно, това разпределение ще се отличава от разпределението на  (което е ) поради замяната .

Без ограничение на общността можем временно да считаме, че (това води до проста транслация по абсцисната ос на търсеното разпределение). Тъй като  ( е броят на степените на свобода), то ясно е, че величината  представлява частно на две случайни величини: тази в числителя има нормално разпределение, а тази в знаменателя е квадратен корен от величина с разпределение . Вероятностната плътност на (5) при условие, че  е:

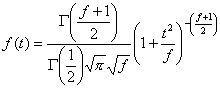                                                                    (6)

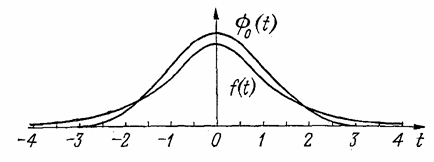
Това разпределение се нарича разпределение на Стюдънт (Student). То е симетрично (четна функция на ) и зависи от един параметър – броя на степените на свобода . При то клони към нормално. На фигурата е показано разпределението на Стюдънт  в сравнение с нормалното разпределение .

Т-критерият (известен още като критерий на Стюдънт) за средната стойност на една случайна величина се прилага така:

·        Приемаме за вярна нулевата хипотеза, че математическото очакване на популацията е ;

·        Избираме ниво на значимост ;

·        намираме границите на критичната област  (разпределението е симетрично и тук имаме двустранен критерий, така че те са две симетрични числа) от условието: ;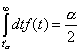

·        правим измерванията, получаваме извадката и пресмятаме статистиката: ;

·        ако , то хипотезата  се отхвърля за нивото на значимост .

 

Този критерий може да се обобщи и да се използува за сравняването на средните стойности на две извадки.

17.2. Т-критерий за сравняване на средните на две извадки

Нека от две популации  и  са направени две извадки с обеми  и . Хипотезата, която ще проверяваме, е, че .

Средните по извадка имат приблизително нормално разпределение (съгласно централната гранична теорема). Техните дисперсии са:

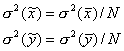                                                                                            (1)

Оценките за дисперсиите от извадката са:

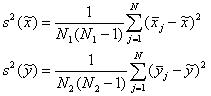                                                                                  (2)

Знаем, че разликата:

                                                                                                           (3)

е също приблизително нормално разпределена и оценката за нейната дисперсия е:

                                                                                       (4)

Ако нашата хипотеза е вярна (), то, очевидно,  и ще е в сила:

                                                                                             (5)

Тогава веднага може да пресметнем вероятността нулевата хипотеза да е вярна, ако е известно. Ние обаче разполагаме само с оценката (4).

Обикновено се предполага, че  и  са от една и съща генерална съвкупност (това във всеки случай е в съгласие с предположението ни за верността на нулевата хипотеза). Тогава:

                                                                                                  (6)

Следователно:

                                                                   (7)

което е претегленото средно на и , е най-добрата оценка за дисперсията на популацията ((7) всъщност е равноправно сумиране на всички индивидуални дисперсии).

В такъв случай:

,                                                                        (8)

Доказва се, че величината:

                                                                                                            (9)

се подчинява на разпределението на Student с степени на свобода.

Този критерий се прилага по-нататък напълно аналогично на критерия на Стюдънт от предния раздел.