2. Третиране на данните с неправдоподобни стойности

Всички системи за събиране на информация внасят лъжливи (грешни) стойности в данните. Добрите системи правят това все пак по-рядко. Това явление може да се дължи на различни причини като частично загубване на сигнали в линиите за връзка, грешки при дискретизацията на сигнала (АЦП), външни електрически смущения и мн.др. При това измежду данните се получават някои резултати със стойности, значително отличаващи се от очакваната последователност, които нямат нищо общо с изследвания процес, но могат да причинят големи неприятности при следващата обработка, още повече ако тя е автоматична. Особено неприятно е наличието на две или повече съседни неверни стойности на данните.

Поради това, първата задача на системите за обработка на данни (след като те бъдат надеждно съхранени в първоначалния им вид!) е издирването и отстраняването на такива данни. За съжаление, много трудно е да се установят общовалидни критерии за това, дали едно число е с очевидно невярна стойност, особено около екстремумите на изследваните зависимости, когато дори “правилното” поведение на данните е трудно да бъде описано, както и в случаите, когато отклонението от действителната стойност не е очебийно голямо. Основното изискване към процедурите, които ще разглеждаме, е те да могат да действуват напълно автоматично и без човешка намеса (както е при масовите анализи).

Най-напред ще посочим какво може да бъде направено след откриването на невярна стойност. Основните възможности са три:

· Измерването да се повтори точно при тези условия и да се използува резултатът от второто измерване. Това обаче е практически неосъществимо в много от случаите, напр. при данните от спектрален тип, когато всички резултати се получават съвместно. Обикновено е по-лесно да се повтори цялото измерване;

· За стойност на дадения канал да се припише някакво по-достоверно число (напр. усреднената по някакъв начин стойност на неговите съседни);

· Съмнителната стойност да не се използува въобще при обработката, (напр. като й се припише нулево относително тегло). Това е от теоретична гледна точка най-правилният подход, тъй като при него единствено не се внасят нови смущения във вида на изследваната функция (а само се намалява получената от експеримента информация).

Всички методи за отстраняване на данни с неправдоподобни стойности изхождат от по-явно или неявно приеманото предположение, че нормалните данни определят една “гладка” зависимост, а ненормалните нарушават тази картина на благополучие. Затова ние трябва да се занимаем най-напред с въпроса за количествения анализ на понятието “гладкост” в разглеждания контекст.

Нека имаме на брой измервания с абсциси и ординати . Еквидистантните стойности на абсцисите, които предполагаме тук за простота, се реализират винаги при данните от спектрален тип, но разглежданията по-долу могат да се пренесат без намаляване на общността и за неравноотстоящи данни (с малко повече писане). Естествено е да търсим количествена мярка за гладкостта на зависимостта в точката чрез локалната кривина на в някаква околност на тази точка. Както е известно от анализа, кривината на една функция в точката се дефинира с:

(1)

където с щрихове са показани първата и втората производна на . Тъй като предполагаме, че извън стойностите на измерванията за функцията не ни е известно нищо, то оценки за нейните производни могат да бъдат направени само чрез апроксимирането им с крайни разлики:

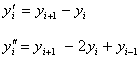(2)

при условие: (Ако данните са неравноотстоящи, (2а) би имало вида:

; (2а')

това подсказва как биха изглеждали обобщенията на разглежданията по-долу за неравноотстоящи абсциси на измерванията).

Преминавайки към нашата задача, ще разгледаме едно семейство числови филтри, основаващи се на минимизацията на локалната кривина (точно тази минимизация на кривината е формалният начин да построим най-гладката зависимост между дадените точки). Тези филтри ще конструираме така:

· За всяка точка филтърът използува стойностите на в точките без точката (която предполагаме, че е съмнителна и подлежаща на проверка);

· , приложен върху , осигурява Това е равносилно на построяването на най-гладката крива през точките и определянето на една изгладена (очаквана) стойност вместо несигурната от стойността на гладката крива - Тук апроксимира кривината в предположение, че измененията на функцията не са много големи . На свой ред, изразът под сумата е средният квадрат на кривината в разглеждания интервал.

И тъй, се дефинира от изискването:

(3)

Това е уравнение за - изгладената стойност, която се получава по стандартната процедура за търсене на минимум от анализа – намиране на производната на спрямо и приравняването й към 0. Полученото равенство разглеждаме като уравнение спрямо търсеното .

Ето как изглеждат последователните членове на това семейство:

. Следователно:

(4)

Това е познатият ни израз за линейна интерполация. С други думи, най-гладката крива, минаваща през две точки - една вляво и една вдясно от разглежданата - е права линия, която в точката има стойността (4).

По-нататък:

. Или:

(5)

Това е линейна екстраполация в посока напред. Следва:

Или:

(6)

Това е квадратична интерполация (една точка напред и две назад). Аналогично се пресмятат и . Сега идва:

Оттук:

(7)

Това е вече квадратично изглаждане (най-добрата парабола през 4 точки – две напред и две назад).

Тъй като производните от втори ред засягат само съседните точки, можем да се убедим, че включването на повече точки не добавя нови членове в това семейство, така че напр. .

Стратегията за търсене на “изхвърчали” точки се формулира така:

· Намираме две съседни точки, за които считаме, че са правилни (започваме от началните точки . Ако някоя измежду точките се окаже с неправдоподобна стойност по следващия критерий, то считаме за съмнителни, отхвърляме ги и караме нататък);

· Образуваме , (от ). Ако: , приемаме, че точката е нормална и продължаваме нататък. Тук ls е мярка за някакво приемливо отклонение. Тя се определя от очакваната неопределеност на данните s, която може да се прецени от допълнителни съображения (с този въпрос ние се занимаваме по-късно; засега ще кажем, че l се избира от порядъка на 3-6). В противен случай следва да направим извода, че поведението на нашата последователност в точката не може да се опише с линейна функция. Тогава имаме две възможности:

· Или е редовен екстремум на функцията (min или max);

· Или e грешна.

За да преценим коя от двете възможности се реализира, образуваме:

(8)

Тук надеждата ни е, че и не са едновременно изхвърчали (или в екстремума). Ако това все пак се окаже така, тази процедура може постепенно да ни отведе далеч от нормалните точки, които в крайна сметка трябва някога да се появят.

Ако , се счита за нормален екстремум и се оставя. В противен случай се счита за "изхвръкнала" точка и се игнорира.

Съблазнително е да се използува филтърът за апроксимация на , тъй като изглаждането дава сигурност спрямо интерполацията (екстраполацията), но съществуват две опасности:

· При се налага да използуваме две непроверени точки едновременно; това увеличава възможността за грешка;

· Изглаждането може да даде лош резултат около екстремумите (голяма разлика , без точката да е с неправдоподобна стойност.

В заключение ще кажем, че противно на правния принцип – “по-добре 10 виновни на свобода, отколкото един невинен в затвора”, за нас е по-добре да изхвърлим повече точки от необходимото, отколкото да оставим една грешна. Такава стойност може да се намеси на много по-късен етап от обработката и да обърка процеса след като вече са положени значителни усилия за пресмятанията. Във всички случаи трябва да сме много внимателни, ако се окаже, че трябва да се изхвърлят последователни точки, а също и около екстремумите на последователностите от данни, защото истинските екстремуми съдържат много важна и необходима информация за поведението на данните.