3. Интерполация и изглаждане на данните

3.1.2. Локална полиномна интерполация. Сплайни

3.1. Интерполация на данните

След като вече сме премахнали данните с груби грешки в стойностите, следващият етап в първичната обработка на данни е да получим възможност да пресмятаме стойностите на данните в междинните точки между измерванията. Съвкупността от методи, използувани за тази цел, се определя с общото название интерполация на данните.

Такава необходимост възниква винаги, когато искаме да търсим екстремуми (минимуми и максимуми) в последователности от непрекъснато изменящи се данни, които, разбира се, едва ли се намират точно при стойностите на аргумента, за които имаме измервания. Понякога ние искаме да разполагаме не само с някакви стойности на самата последователност, но и с нейните производни в междинни точки или интеграли в някакъв интервал от стойности на аргумента. Във всички такива случаи ние трябва да разполагаме с някакъв алгоритъм за интерполация. Разбира се, интерполацията се използува не само при обработката на експериментални данни, но и при моделирането на данни, когато в някои случаи пресмятането на пълния модел в достатъчен брой точки изисква големи изчислителни усилия. Тогава съчетаването на пълни пресмятания в ограничен брой точки с подходяща интерполационна процедура може да ускори многократно решаването на цялостния проблем.

Формално задачата за интерполация се формулира така:

Нека са дадени една съвкупност от реални абсциси и стойности на ординатите . Задачата на едномерната интерполация се състои в това, да се построи функция такава, че за всяко и да има някакви приемливи стойности между стойностите .

Разбира се, същината на задачата за интерполация е дефинирането на "разумното" поведение на интерполиращата функция в междинните точки. Очевидно зададените точки могат да бъдат интерполирани по безброй много начини и ние трябва да имаме критерии за избор между тях. Обикновено критериите за избор се формулират в понятия като простота и гладкост на представянето - напр. да бъде диференцируема и с непрекъснати производни до определен ред в целия интервал, или да бъде възможно най-гладка в този интервал, или да бъде полином от най-малка степен и т.н.

Класически пример за интерполация е полиномната интерполация, която ще си припомним накратко.

3.1.1. Полиномна интерполация

Множеството от алгебрични полиноми е най-важният клас интерполационни функции поради някои свои особено благоприятни свойства. Знаем, че полиномите лесно се пресмятат, събират, умножават, диференцират и интегрират, полиномите от полиноми също са полиноми и т.н.

Полиномите са подходящи за апроксимация (и в частност за интерполация) на функции поради обстоятелството, че всяка непрекъсната функция може да се апроксимира с произволна точност върху всеки краен затворен интервал чрез полином (теорема на Вайерщрас (Weierstrass) за апроксимация: ако e непрекъсната функция върху крайния затворен интервал , за всяко съществува полином от степен такъв, че ).

Разбира се, степента на такъв апроксимиращ полином зависи от желаната точност на апроксимацията (измервана с числото ). Тази степен може да е толкова висока, че полиномът да е практически неизползуваем.

Всеки полином може да се представи в ред по степените на :

. (1)

Този ред има коефициенти. За да бъдат определени тези коефициенти еднозначно, необходимо е да се определят независими условия. При интерполация обикновено се иска полиномът да минава през всичките (различни) точки . Това води до система от линейни алгебрични уравнения:

, (2)

които трябва да бъдат решени относно неизвестните коефициенти . На нас ни е известно, че такава система има единствено решение. Така че винаги е възможно прекарването на единствен полином от степен през всеки различни абсциси . Такъв подход, при който цялата съвкупност данни се интерполира с една единствена функция, се нарича глобална интерполация.

След като сме решили да интерполираме данните глобално с полином от степен, ние все още имаме свободата да изберем базисните функции, които трябва да принадлежат на пространството на полиномите от степен . В написаното по-горе използувахме най-простия полиномен базис - от едночлените . Системата линейните уравнения (2) може по принцип да бъде решена с някой от числените методи на линейната алгебра (например чрез Гаусово (Gauss) елиминиране). Проблемът е, че в много случаи тези системи уравнения са твърде лошо обусловени (с други думи, решенията им са много чувствителни към грешки от закръгляване). Тази чувствителност е толкова силна, че практически подобни линейни системи се решават с трудности дори за .

Един много по-приемлив начин за построяване на интерполационен полином е за базис да се използуват известните полиноми на Лагранж (Lagrange). За разлика от разгледаните едночлени, тези полиноми се построяват специфично за всяко конкретно множество от точки . Те имат свойството:

. (3)

Вижда се, че полиномът:

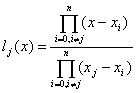(4)

удовлетворява тези условия (всеки множител в числителя анулира полинома за някое ; множителите в знаменателя са за нормировка, за да осигурят условието ). Тъй като има само един такъв полином, ясно е, че именно е полиномът с тези свойства. Интерполиращата функция, представена чрез полиномите на Лагранж, има вида:

(5)

Тази функция има във всяко стойност точно .

Тук трябва още веднъж да кажем, че полиномът от степен , който минава през всичките точки, е единствен. Има различни полиномни интерполационни формули, построени върху различни базиси (напр. (2) и (5)), но при еднаква съвкупност от данни те всичките водят до един и същ полином. Различните представяния на този полином обаче могат да имат много различно поведение при пресмятания с ограничена аритметична точност, каквато е всяка машинна аритметика. В този смисъл интерполационният полином на Лагранж (или някой друг подобен) е за предпочитане пред интерполацията, основана на базис от едночлените на аргумента.

В крайна сметка, въпреки своята простота, полиномната интерполация има много недостатъци. Те са свързани основно с:

· необходимостта от пресмятания на полиноми от висока степен, които увеличават изчислителните усилия;

· трудности, свързани с грешките от закръгляване;

· лошо поведение извън краищата на интервала (известно е, че асимптотично полиномите клонят към ±¥ при неограничено нарастване (както и намаляване) на аргумента, което не е така за реално съществуващите данни от физични измервания. Ето защо интерполационните полиноми в никакъв случай не трябва да се използуват за екстраполация на данните извън интервала;

· Вътре в самия интервал пък полиномите (особено тези от висок ред) могат да имат осцилации, които да са толкова големи, че да се обезсмисля възможността те да бъдат използувани за пресмятане на междинни стойности на данните.

Недостатъците на глобалната полиномна интерполация могат да бъдат значително редуцирани чрез използуването на локална полиномна интерполация.

3.1.2. Локална полиномна интерполация. Сплайни

Основната идея на локалната полиномна интерполация е да се използуват полиноми от сравнително ниска (3, 4,... до 10) степен, които да минават през няколко съседни точки; след това част от тези точки се отнемат отляво, а отдясно се прибавят други точки, това множество се интерполира с друг полином от подобна невисока степен и този процес продължава, докато се изчерпят всичките точки от разглежданата последователност. Такива построения се наричат още "плаващи полиноми".

Тъй като сплайните представляват по-нататъшно развитие на локалната полиномна апроксимация, което отразява и съвременното състояние на проблема, ние ще разглеждаме именно тях.

Първите сплайн-функции са предложени от Шьонберг (I.J.Schоenberg) (1946) и са били "слепени" от отделни парчета от кубични полиноми. Тази конструкция се е развивала и модифицирала чрез повишаване на степента на полиномите, промяна на условията във възлите и по границите и т.н. Съществен прогрес в развитието на теорията на сплайн-функциите е свързан с името на Холидей (J.C.Holladay)(1957), който е свързал сплайните с решаването на вариационна задача за минимума на потенциалната енергия на огъване на еластичен прът. Това е дало възможност по-нататъшните конструкции на сплайни да се свързват с различни вариационни задачи, отразяващи конкретните физични модели, свързани с произхода на данните.

Ние ще разгледаме по-подробно построяването на класическите кубични сплайни на Шьонберг.

Има смисъл да започнем разглеждането на сплайни именно от аналогията на тези функции с формите на еластичните пръти, каквито са били използувани отдавна от чертожниците за построяване на криви (оттам произлиза и наименованието "spline"). Механичният сплайн се закрепва (с помощта на тежести) в точките на интерполация (възлите) и при това той приема такава форма, че потенциалната му енергия е минимална. От механиката е известно, че тази потенциална енергия е пропорционална на линейния интеграл по дължината на дъгата от квадрата на кривината на сплайна.

Нека сплайнът се представя с функцията . Ако наклонът на тази функция не е голям, ние знаем, че кривината се апроксимира с втората производна на функцията . Следователно енергията на подобен линеаризиран сплайн е пропорционална на .

Формално задачата се дефинира така:

Дадени са абсцисите и ординатите . Искаме да построим такава функция , че и 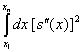да е минимален.

Продължавайки аналогията с механичния сплайн, ние можем да очакваме и да бъдат непрекъснати във възлите (иначе механичният сплайн ще се счупи). По-нататък от механиката следва, че между всеки два възела е полином от трета степен и във всеки от възлите преходът между съседните полиноми се осъществява така, че , и са непрекъснати.

Доказано е, че ако към тези условия се прибавят условията по краищата: (такава функция се нарича естествен кубичен сплайн), то тази функция е единствената функция (забележете: не само полином!), която има минимална кривина измежду всички функции, които интерполират данните и имат втора производна с интегрируем квадрат. В този смисъл може да се каже, че естественият кубичен сплайн е най-гладката функция, която интерполира множеството от данните.

Колко са всичките параметри на кубичния сплайн? Между възлите има интервала и в тях има части от кубични полиноми, всяка с по 4 параметъра. Следователно трябва да се наложат общо условия, за да се определят еднозначно параметрите на сплайна. Условията за непрекъснатост на , и във вътрешните точки дават условия. Условието дава още условия за (дотук общо ). Необходими са още две условия за пълното определяне на сплайна. Ако приемем (това е равносилно на предположението, че извън множеството от данни сплайнът е линейна функция), то получаваме естествения кубичен сплайн, за който вече стана дума. Разбира се, вместо тези две условия може да се наложат някакви други две условия.

Сега ще видим как се построява кубичен сплайн. Разглеждаме кривата в подинтервала . Общият вид на сплайна в този подинтервал е:

(1)

Нека да означим: . (2)

Удобството на тези означения е, че когато се мени в този интервал, се мени от 0 до 1, а - от 1 до 0. В тези означения е подходящо да представим сплайна във вида:

, (3)

където s_i+1и s_iса константи, подлежащи на определяне. Първите два члена в (3) определят стандартна линейна интерполация, а членът в квадратните скоби е корекция от трета степен, която се анулира и в двата края на подинтервала. Така че (3) осигурява интерполация на данните независимо от избора на s. Ние обаче ще определим константите {s_i} така, че да осигурим необходимата гладкост на сплайна.

Сега ще диференцираме три пъти по , за да можем да наложим необходимите условия за гладкост:

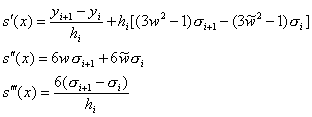(4)

Нека да пресметнем в краищата на подинтервала, като вземем предвид, че тъй като е дефинирана само в затворения подинтервал , то на границите имаме само едностранни производни - отдясно за лявата граница и отляво за дясната граница:

(5)

Тук: (6)

За да получим търсената непрекъснатост на първата производна , необходимо е да бъде изпълнено условието двете едностранни производни на всички вътрешни граници на подинтервалите да са равни:

(7)

(При това непрекъснатостта на се получава автоматично). Това условие води до уравнението:

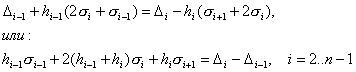(8)

Това е система от уравнения за неизвестни . Необходимо е да се формулират още две допълнителни условия, за да бъде определен интерполационният сплайн по единствен начин. Тези условия в естествения кубичен сплайн са, както вече писахме:

(9)

Общият вид на системата линейни уравнения (8) в матричен вид изглежда така:

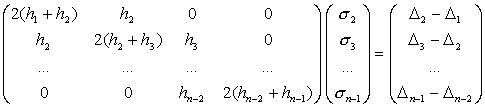(10)

Тази система от уравнения лесно може да се реши, макар че тя може да бъде от висок ред. Основание за това ни дава специалният вид на матрицата от коефициентите на системата. Тя има следните особени свойства:

· матрицата е лентова (тридиагонална);

· матрицата е симетрична;

· тази матрица е неособена и е положително дефинитна (= с доминиращи елементи по главния диагонал).

Такива системи линейни уравнения се решават лесно по метода на Холецки (Cholesky), чиято схема накратко привеждаме:

За всяка реална симетрична положително дефинитна матрица съществува, и при това единствено, представяне:

, (11)

където е лява (долна) триъгълна матрица, а с е означена транспонираната й матрица. Тогава в системата: можем да означим:

и да заменим нейното решаване с последователното решаване на двете системи:

. (12)

(първо намираме междинното неизвестно , а след това и търсеното ). Предимството на тази замяна е обстоятелството, че системи линейни алгебрични уравнения с триъгълни матрици се решават много просто с последователно заместване (отгоре надолу за лява триъгълна матрица и отдолу нагоре за дясна триъгълна матрица).

Връзката между коефициентите и коефициентите е:

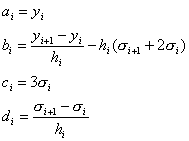(13)

Представянето на коефициентите във вида (13) дава възможност по-лесно да се пресмятат производните и интегралите на сплайна.

3.2. Изглаждане на данните

При интерполацията ние предполагаме, че стойностите на данните в точките на измерване са точни и нашата задача е да получим възможност да пресмятаме тези данни при междинни стойности на аргумента. В действителност ние много рядко можем да считаме, че измерванията са с толкова висока точност, че да е разумно данните да минават тъкмо през експериментално измерените стойности. Обикновено измерванията са съпроводени със значителни грешки или неопределености. Те понякога са толкова големи (в една наглед шеговита книга се съдържа следният мъдър съвет: “много рядко има измервания с точност, по-добра от 1%, независимо от уверенията на авторите им”), че простата интерполация на такива данни води до решения, които са математически коректни, но нямат никакъв физичен смисъл.

В т акива случаи ние се нуждаем от по-сложни процедури, които да ни позволят да получим една изгладена последователност от числови данни, минаваща плавно покрай експерименталните наблюдения.

Защо е нужно такова изглаждане? Има няколко причини за това:

· Първо, то съответствува на интуитивната ни представа, че физичните закономерности са по природата си гладки и ако наблюдаемите зависимости не са такива, то причината е в случайните фактори, влияещи върху измерванията. Те водят до данни, съдържащи грешки от случаен характер, които трябва да бъдат “поправени” с подходяща процедура за изглаждане. Най-често ситуацията е именно такава в смисъл, че измерваните зависимости са наистина гладки. Трябва обаче да знаем, че има някои важни изключения, главно от областта на атомната и ядрената физика, където има множество наблюдаеми величини, чиито стойности се изменят дискретно (например атомните и ядрените спектри на излъчване и поглъщане);

· Второ, изгладените зависимости позволяват да се разграничат по-добре съществените особености на данните от несъществените детайли, които понякога (при големи грешки) дори могат да маскират основната закономерност, която представлява интерес за нас;

· Накрая, изгладените зависимости имат по-добри качества от гледна точка на числения анализ, в частност те позволяват да се получат по-достоверни резултати при числено диференциране, при търсене на минимуми и максимуми и др.

Като математически обекти методите за изглаждане представляват оператори, т.е. правила, по които на всяка функция (последователност от данни) се съпоставя друга функция (изгладена последователност). Физичната природа на наблюденията обикновено изисква тези оператори да са линейни, т.е.

(1)

(такива са и самите наблюдения, например спектърът на смес от няколко вещества е суперпозиция от спектрите на отделните вещества в първо приближение). Ако означим наблюденията с , а изгладената последователност с , то най-простият вид на един оператор на изглаждане има вида:

. (2)

Прости примери за изглаждащи оператори са изглаждането по три точки с еднакви тегла (т.нар. пълзящо средно):

(3)

или пък с различни тегла, например:

(4)

Изглаждането, описвано с правилото (3), е по-силно от това с (4), тъй като в последното относителното влияние (тегло) на изглажданата точка е по-голямо (затова и изглаждането (4) е по-слабо). Очевидно крайната ситуация (най-слабо изглаждане) в това отношение е:

, (5)

което, разбира се, не е никакво изглаждане.

Описаните правила (3) и (4) са прости (и се използуват много често), но техният основен недостатък е, че те третират всички точки в изглажданата последователност по еднообразен начин, без да отчитат различната степен на гладкост на зависимостта в отделните й участъци.

Тук трябва да уточним, че когато делим опитно измерваните зависимости на дискретни и непрекъснати, някои от тези закономерности са по природата си дискретни, но те се наблюдават като непрекъснати благодарение на:

· фона от непрекъснати взаимодействия, които неизбежно присъствуват в измерванията и се наслагват върху полезния сигнал (който може да е дискретен);

· несъвършенствата на детекторите, които пораждат функция на отклика с непрекъснат характер въпреки дискретната природа на въздействието.

От тази гледна точка, основните типове данни се делят на такива, които са по природа непрекъснати и такива, които са квазинепрекъснати в горния смисъл. Истински непрекъснатите зависимости се описват обикновено с толкова гладки функции, че съответните експериментални данни могат да бъдат успешно изгладени с почти всякакви методи за изглаждане, дори и толкова прости като описаните по-горе. Затруднения при изглаждането се проявяват именно при зависимостите, които не са много гладки. Проблемът се състои в това, да се конструира такъв метод за изглаждане, който да осъществява филтриране на шума от статистическия характер на измерването и същевременно да запазва особеностите, присъщи на наблюдаваните закономерности. Обикновено използуваните методи за изглаждане се провалят именно около участъците с малка гладкост, каквито са около пиковете, минимумите и другите особености на последователностите от данни.

Ние ще разгледаме един такъв общ метод за изглаждане, който е описан най-пълно от В.Б.Злоказов (1980), макар че в различни форми е срещан и по-рано. Той се състои в следното:

Въвежда се мярка за осцилацията на една функция. На визуално наблюдаваната осцилация съответствува бързо изменение на нормата на първата й производна, както и на нейния знак. Ако се сравнят два участъка от една крива, на които първата производна се променя еднакво, ние сме склонни да считаме за по-бързо променящ се този участък, който има по-малка дължина. Така че за мярка на осцилацията на функцията в един безкрайно малък интервал се приема отношението на изменението на първата й производна към дължината на кривата в този интервал, което е точно известната ни вече кривина:

(6)

Интегралната мярка за осцилация на функцията в даден интервал се определя като:

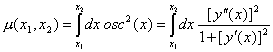(7)

Така определената интегрална величина m е квадратична мярка, която съответствува на нагледната ни представа за осцилация.

Сега задачата за изглаждане се формулира така:

Нека имаме наблюденията , които предполагаме, че са еквидистантни за простота на записа. Ако с означим изгладената последователност, то ние искаме тя да се конструира от условието да се намери минимумът на функционала:

. (8)

Смисълът на така конструирания функционал е следният: той се състои от два члена, от които първият е (квадратична) мярка за осцилацията на изгладената функция, а вторият е (също квадратична) мярка за близостта на изгладената последователност до оригиналните наблюдения. И тъй, ние искаме с конструирането на да постигнем две цели - хем изгладената последователност да е близо до експерименталните точки, хем тя да има минимална осцилация. Лесно е да се убедим, че тези изисквания са противоречиви. Големината на числото , което ние можем свободно да избираме, е мярка за компромиса между тези две условия, който ние правим. Ако искаме изгладената последователност да бъде по-гладка, e трябва да се увеличава; ако пък искаме да е по-близо до , трябва да намалява. Граничните случаи са, очевидно:

· , когато се получава баналното решение (т.е. функцията ще минава точно през наблюденията , но няма да има никакво изглаждане), или

· e®¥, когато трябва да клони към 0, за да има крайно решение. Това е еквивалентно на изискването функцията да клони към права линия. Така ще получим най-гладката функция, която изобщо може да се построи, но която, разбира се, изобщо не е длъжна да минава близо до нашите наблюдения, респ. да служи за изглаждане на тези данни.

Между тези гранични случаи ние сме свободни в избора на изглаждащия параметър в зависимост от нашите предпочитания и вида на поставената задача.

За да се допълни така формулираната задача за изглаждане, трябва да се прибавят гранични условия за краищата:

(9)

Този избор на гранични условия всъщност изразява липсата на информация за гладкостта на търсената зависимост в крайните точки. Поради това ние предполагаме линейно поведение на тази функция в краищата на интервала и по посока извън него.

Сега минаваме към дискретния аналог на съотношението (8), като си даваме сметка, че ние познаваме изглажданите данни само в точките, където имаме измервания. Първо опростяваме израза за осцилацията, тъй като в него влиза силно нелинейно (чрез знаменателя). Да си спомним, че при конструирането на изглаждащи филтри за анализиране на данните с неправдоподобни стойности ние приехме . Тогава ставаше въпрос за заключения от качествен характер и това приближение беше оправдано. Сега не можем да се задоволим с толкова грубо приближение; затова ние заместваме израза в знаменателя с някаква апроксимация на дължината на дъгата, която да не зависи от . Най-добре е като приближение на да използуваме самите наблюдения (тъй като ние искаме в крайна сметка да е близо до ). Така знаменателят става независим от и задачата за минимизация става линейна.

И така, уравнението за определяне на добива вида:

, (10)

където:

. (11)

Тук трябва още веднъж да изтъкнем, че линейността на задачата се осигурява от замяната с . Тя се оправдава от обстоятелството, че при неголям статистически шум в данните е сравнително добра апроксимация на и като се има предвид, че тази замяна се прави само в теглото на единия член на функционала , тази апроксимация в много случаи е приемлива. Това приближение е обаче само за наше удобство. Ако това заместване не води до добри резултати, възможно е задачата да се реши по-точно, като се организира итерационен процес, в нулевата итерация на който се използува приближението (11), а в следващите – стойността на изгладената последователност от предишната итерация:

. (12)

Практически това рядко се налага, като се има предвид, че все пак става дума за първична обработка на данните.

За да намерим минимума на функционала , трябва да приравним на нула всички негови първи частни производни спрямо параметрите , които се явяват в тази задача неизвестни величини, подлежащи на определяне.

Ето тези производни:

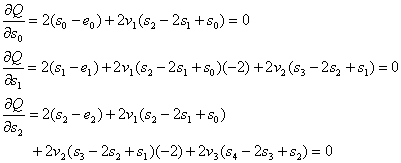(13)

Общият член е:

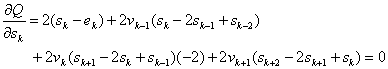(14)

Като прегрупираме членовете пред неизвестните {s_k}, получаваме:

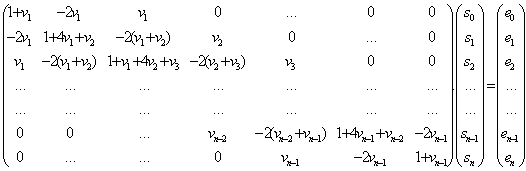(15)

Това е линейна система алгебрични уравнения и техният брой е твърде голям (колкото е броят на измерванията, често от порядъка на хиляди). Тази система обаче притежава отново особено благоприятните свойства на системата от предишния раздел, а именно:

· матрицата на системата (15) е реална и симетрична;

· тя е с доминиращ главен диагонал (=положително дефинитна).

· тази матрица в допълнение е лентова матрица с ненулеви елементи само по главния диагонал и съседните му два кодиагонала.

Това позволява за решаването на тази система отново да се използува разложението на Холецки, което е много рационално по отношение на числените пресмятания.

Да добавим, че стойността на параметъра по принцип е свързана с точността на измерванията . В ситуацията на първична обработка на данни, когато ние практически нямаме информация за статистическите свойства на данните, стойността на този регулиращ параметър обикновено се избира въз основа на тестове.

Трябва да споменем още няколко неща във връзка с този метод:

· при него ние получаваме стойностите на изгладената последователност само в точките на измерванията . Ако са ни необходими интерполации за междинни стойности, ние можем да използуваме например сплайнова интерполация, построена върху стойностите на изгладената последователност ;

· Решаването на задачата за изглаждане на данните по описания по-горе метод е непосредствено свързано и много сходно с подхода, използуван при конструирането на сплайнова интерполация. Ние можем да търсим директно решение на задачата за изглаждане чрез сплайни; такива сплайни се наричат апроксимационни сплайни. Решаването на такава задача обаче е по-сложно и излиза вън от рамките на този курс.

Литература:

[1]. Дж. Форсайт, М.Малкълм, К.Молър: Компютърни методи за математически пресмятания, Наука и изкуство, София (1986).

[2]. В.Б.Злоказов, Метод для автоматического поиска пиков в гамма-спектрах, Препринт Р10-81-204, ОИЯИ-Дубна (1981).