5. Търсене на пикове в спектрите

Тук ще говорим условно за “спектри”, т.е. за последователности от данни с еквидистантни стойности на аргумента.

Както вече отбелязахме, пиковете са области от спектрите, които съдържат съществената информация, заради която спектрите са измерени. Поради това откриването на пикове в един спектър е една важна част от предварителната му обработка. Тук ще се спрем накратко на методите за автоматично търсене на пикове.

Основните методи, по които се търсят пикове в данните, са два:

·        чрез използуване на екстремалните свойства на пиковете (известни от математическия анализ). При това се построяват апроксимации за първата (а понякога и за втората) производна на наблюденията (след като те са вече изгладени и фонът е изваден);

·        чрез използуване на корелациите между последователните стойности на спектралните данни в областта на пиковете.

 

Методът на производните се основава на обстоятелството, че в областта на пика първата производна на данните спрямо аргумента се променя съществено, като преди пика тя е слабо положителна, после значително се увеличава, след което намалява, минава през нулата и след това симетрично се изменя, минавайки през минимум и асимптотично отива пак към нула, оставайки отрицателна. Пикът се намира при междинното й нулиране. Втората производна пък (тъй като е мярка за кривината) в областта на пика добива съществено отрицателни стойности, които са заобиколени от двете страни симетрично с положителни стойности.

Тези функции имат твърде характерно поведение, което служи за идентификация на пика. Основна пречка за използуването на този метод е статистическият шум в данните, който ограничава възможността за откриване на слаби пикове, тъй като влияе върху стабилното определяне на първата и особено на втората производна, въпреки междинното числено изглаждане на данните, което обикновено се предприема. Картината се усложнява значително в случай, че има два или повече пикове в близост (мултиплетни структури), особено ако те не могат да бъдат разделени от регистриращата апаратура (вж. фигурата). Комбинирането на критериите на първата и втората производна помага за по-сигурното определяне на наличието или отсъствието на пик в спектъра.

 

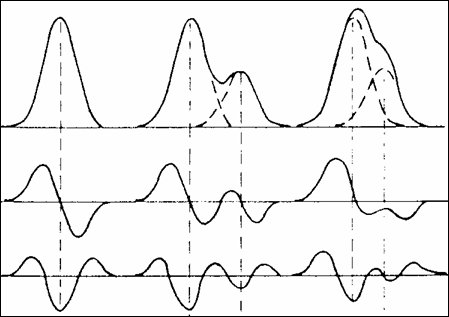
                  единичен пик             частично разделен               неразделен

                                                           дублет                             дублет

Поведение на y(x), y’(x) и y”(x) около максимум

 

Корелационният метод за търсене на пикове се основава индиректно на локалната кривина на спектъра и изменението й в областта на пика. За да се пресметне промяната в наклона, необходимо е да се филтрира високочестотният статистически шум, което става обикновено чрез усредняване по няколко канала в рамките на ширината на линията. За целта се използува трансформация от вида:

                                                              (1)

където  е подходящо избрана функция-филтър. Към нея има две изисквания:

·        тя трябва да има нулева площ;

·        и да бъде симетрична относно центъра си.

При наличие на пик  приема голяма положителна стойност (пропорционална на площта на пика). В отсъствие на пикове  флуктуира около нулата.

Най-често използуваните корелационни филтри са:

 

 

 

 

 

 

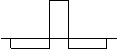
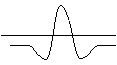
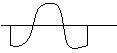
квадратична                        правоъгълна             обърната втора            Гаусов

     вълна                                      вълна                        производна             корелатор

                                                                              на Гаусова функция

 

Общо взето, и четирите функции дават сходни резултати при търсенето на пикове. Последните две имат известни предимства по отношение на точност, но с първите две пресмятанията се извършват по-бързо.

Основно предимство на корелационния метод пред метода на производните е, че тук за идентифициране на пика се използува информацията едновременно от много точки около него. Това придава на този метод стабилност, присъща на всички изглаждащи методи. Известен недостатък на корелационния метод обаче е необходимостта от предварителна оценка на ширината на търсените пикове.

 

При излагането на тези методи ние съзнателно оставяме открит въпроса за пиковите мултиплети, т.е. за недобре разграничените един от друг близки пикове. Такива конфигурации внасят допълнително усложняване на картината и затрудняват откриването на пикове. В известна степен обаче изложените тук методи могат с някои модификации да бъдат прилагани и в такива случаи.

 

Накрая, след като един пик е идентифициран като възможен според горните критерии, е необходимо да се провери неговата статистическа значимост. Това става най-общо чрез сравняване на амплитудата (или по-добре – на площта) на пика с флуктуациите на фона в тази област. Решаването на тази задача обаче (както и при останалите методи за обработка на данни) не е възможно без използуването на информация за статистическия характер на обработваните данни.

 

Литература:

[1]. G.W.Philips, K.W.Marlow, Nucl.Instr.Meth. 137 (1976) 525-536.