6. Случайни величини

 

   6.1. Понятие за вероятност

   6.2. Случайни величини. Разпределения на случайните величини

   6.3. Функции на случайни величини. Математическо очакване. Дисперсия. Моменти

   6.4. Свойства на математическото очакване и дисперсията

 

 

 

6.1. Понятие за вероятност

Експериментът се дефинира като строга последователност от предварително определени действия, водещи до определяне на стойностите на една (или повече) величини, които се наричат резултат(и) от експеримента. Те могат да се изменят дискретно или непрекъснато.

Независимо от точността на изпълнение на условията за провеждане на експеримента обаче, резултатите от повторния експеримент са, изобщо казано, различни. Това се дължи или на ограничената точност на измерванията, или на вътрешната природа на изследваното явление.

Поради това, възможните стойности на всяка величина, която е резултат от един експеримент, не са някакви фиксирани числа, а някакво (най-често ограничено) множество. Съвкупността от тези области за всички величини, представляващи резултати от даден експеримент, се нарича пространство на извадките (основно пространство) на този експеримент. Обикновено е трудно да се определят точните граници на допустимите области за всички величини, които са измеряеми в даден експеримент. Затова обикновено пространството на извадките се взема по-голямо и то съдържа фактическото пространство като подмножество.

Елементарно събитие се нарича всеки елемент от пространството на извадките, т.е. всяка реализация на експеримента, при която се получават определени конкретни резултати за всички величини в този експеримент.

Събитие се нарича пък фактът на принадлежност на резултата към някакво подмножество на пространството на извадките. Ако едно събитие  не е настъпило, ние говорим за настъпването на допълнителното събитие . Цялото пространство на извадките пък съответствува на събитие, което се случва винаги в резултат на този експеримент (сигурно или достоверно събитие - ).

Понятието вероятност на дадено събитие  има различни определения:

·        честотно - като граница на отношението на броя на благоприятните изходи за събитието към общия брой реализации на експеримента: . Трудностите с употребата на това определение са свързани с невъзможността за провеждането на безкраен брой експерименти;

·        вероятността може да се въведе и аксиоматично (Колмогоров) чрез един минимален брой аксиоми. Тук ние ще ги скицираме:

1.      (неотрицателност): На всяко събитие  съответствува неотрицателно число, което се нарича негова вероятност: ;

2.      (нормировка): Достоверното събитие  има вероятност единица: ;

3.      (адитивност): Ако събитията  и  са несъвместни (не могат да се случат едновременно), то вероятността за настъпване на  или  е: ;

4.      (непрекъснатост): За всяка редица от събития, клоняща към празното множество, редицата от техните вероятности е сходяща с граница 0: .

 

От тези аксиоми лесно се получава като следствие например, че .

Условната вероятност да се случи събитието  при условие, че вече е настъпило събитието , се определя така:

Оттук:

В тези изрази  е сечението на събитието  със събитието .

Оттук следва формулата за пълната вероятност за дадено събитие:

Нека даден експеримент води към някое от следните несъвместни събития:

Тогава вероятността да се осъществи кое да е събитие  е:

.

Верността на това равенство следва от предишните разглеждания.

 

6.2. Случайни величини. Разпределения на случайните величини

Всяко събитие може да се характеризира чрез получаването в резултат на настъпването му на една от възможните стойности на някаква величина. Тъй като при всяка реализация на един експеримент тази величина приема различни стойности (които са неизвестни отнапред), тя се нарича случайна. Случайните величини се делят на дискретни или непрекъснати според множествата от стойности, които могат да заемат.

Основната характеристика на всяка случайна величина е нейната функция на разпределение. Тя се определя така:

ако  е случайна величина и е реално число, то вероятността за събитието () е функция на  и се нарича функция на вероятностното разпределение на случайната величина :

.                                                                                               (1)

Ако   е дискретна случайна величина,  е стъпаловидна функция. Очевидно  е монотонно ненамаляваща функция.

От определението следва:

                                                                    (2)

Специален интерес представлява не само (и не толкова) функцията , а нейната производна по аргумента й:

,                                                                                                   (3)

която се нарича плътност на вероятностното разпределение (вероятностна плътност) на случайната величина . Тя е пропорционална на вероятността за събитието - след експеримента случайната величина  да се окаже в един безкрайно малък интервал около числото . Очевидно:

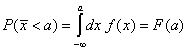                                                                             (4)

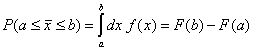                                                            (5)

В частност:

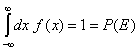                                                                                         (6)

6.3. Функции на случайни величини. Математическо очакване. Дисперсия. Моменти

Често ние се интересуваме освен от дадена случайна величина още и от някаква функция на тази случайна величина. Всяка функция от една случайна величина е също случайна величина, доколкото също заема различни стойности при различни реализации на един и същ експеримент. Следователно тя има също вероятностна функция на разпределение, както и вероятностна плътност.

Средна стойност (математическо очакване) на една дискретна случайна величина се нарича сумата от всевъзможните стойности на тази величина, умножени по съответните им вероятности:

                                                                                        (1)

Средната стойност на случайната величина обаче не е случайна величина. Тя всъщност не зависи от , тъй като в (1) се сумира по всички възможни стойности на случайната величина. Средната стойност не е функция, а функционал на , т.е. правило, по което на една функция –, се съпоставя едно число – математическото очакване.

Средна стойност на функцията  на случайната величина  се определя така:

                                                                         (2)

При непрекъснати случайни величини тези формули се обобщават непосредствено:

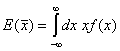                                                                                             (3)

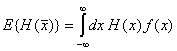                                                                               (4)

Сега ще разгледаме една функция от специален вид:

                                                                                                 (5)

Нейното математическо очакване:

                                                                                               (6)

се нарича момент от ранг к на случайната величина  спрямо точката .

Особен интерес представляват моментите спрямо средната стойност на случайната величина:

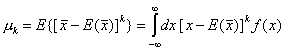                                                    (7)

Те се наричат централни моменти на случайната величина . Причината за специалното предпочитание към централните моменти се основава на обстоятелството, че функцията  има минимум при поне при .

 Очевидно,  е низшият по порядък централен момент, който съдържа информация за отклонението на случайната величина от средната й стойност. Централният момент от втори порядък  се нарича дисперсия на случайната величина . Ето няколко синонимни означения, използувани в различни книги:

Моментите на случайните величини имат и физична интерпретация:

При множество измервания на една и съща случайна величина резултатите се групират предимно около една “истинска” стойност на тази величина. Или, казано по-точно, по-вероятно е да се получат (и по-често се получават) стойности, близо до някакво число (напр. ), отколкото далеч от него. Вероятностната плътност на случайната величина тогава ще има типичната и често срещана  камбановидна форма. Математическото очакване може да се интерпретира като оценка за действителната стойност на измеряемата величина. Изразът за него прилича на този за координатите на центъра на масите на едно (едномерно) тяло. Дисперсията пък в такъв случай може да се интерпретира като израз за инерчния момент на такова тяло (относно центъра на масите му), и тя е мярка за разсейването на резултатите от измерванията около средната им стойност. Ако дисперсията е малка, измерванията могат да се считат за по-точни (по-голяма част от тях са близо до средната стойност).

Дисперсията е квадратична мярка. Затова се използува величината , която се нарича средноквадратично (стандартно) отклонение на случайната величина . Обикновено именно тази величина се посочва като мярка за грешката (правилният термин е статистическата неопределеност) на  и се пише: .

В много случаи математическото очакване и дисперсията не дават достатъчна информация за изследваните случайни величини; затова за по-пълното им характеризиране се използуват и моменти от по-висок ред.

Третият централен момент  характеризира несиметричността на вероятностното разпределение около математическото очакване. Прието е безразмерната величина

                                                                                                             (8)

да се използува за количествена характеристика на различията между относителния дял на положителните и отрицателните отклонения от средната стойност. Тази величина се нарича асиметрия (skewness) на разпределението на случайната величина. За симетрични разпределения (които се представят с четни функции на вероятностната плътност) .

Четвъртият централен момент  определя характера на максимума в точката на математическото очакване при симетрични разпределения. За количествена характеристика се приема безразмерната величина

                                                                                                       (9)

която се нарича ексцес (kurtosis).

Величините асиметрия и ексцес са въведени чрез равенствата (8) и (9) така, че за най-често срещаното разпределение - нормалното - те да са нули: , . При  по-голямата част от вероятностното разпределение се намира вдясно от математическото очакване (респ. обратното). При  пък максимумът на вероятностната плътност е по-остър от този при нормалното разпределение с параметри като в равенството (9), съответно при  максимумът на разпределението е по-тъп от този на нормалното разпределение.

По-висшите моменти на разпределенията рядко се използуват. Трябва да се отбележи, че колкото по-голям е рангът  на даден момент, толкова по-голям е приносът на отдалечените от средната стойност участъци от функцията на вероятностната плътност (тъй наречените "опашки" на разпределението) при определянето на к-ия момент.

Освен важността на отделните моменти, съществено теоретично значение има и пълният набор от всички моменти (централни или нецентрални) на даденото разпределение. Нецентралните моменти се дефинират така:

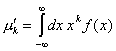                                                                                                          (10)

Доказва се (това ще видим малко по-нататък), че при много общи условия (които са изпълнени за всички разпределения, представляващи практически интерес) съвкупността от всички моменти напълно определя вероятностното разпределение. Има случаи, когато е по-лесно да се построят моментите на едно неизвестно разпределение, отколкото самото разпределение (т.е. вероятностната му плътност). Това позволява тогава да се построи и самото разпределение чрез неговите моменти.

В сила е по-конкретно следното твърдение (теорема):

Ако  и  са две вероятностни плътности, всичките съответни нецентрални моменти на които са равни, и ако разликата  е разложима в степенен ред, то .

Ние ще установим верността на това твърдение. Нека означим:

 и нека моментите на двете функции са съответно

Тогава:

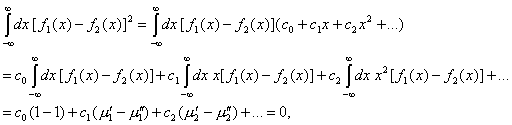
откъдето следва, че  (тъй като подинтегралната функция е неотрицателна и тогава горният интеграл е 0 тогава и само тогава, когато самата подинтегрална функция е тъждествено равна на нула).

При зададена вероятностна плътност  пресмятането на моментите не представлява проблем. Проблем представлява обаче често самото намиране на вероятностната плътност, която да описва адекватно процеса на измерването на изучаваната случайна величина.

6.4. Свойства на математическото очакване и дисперсията

1. Ако , то:

                                                                                                   (1)

                                                                                             (2)

От последното равенство следва:

                      (3)

 

2. Разглеждаме функцията

                                                                                                     (4)

Тази функция е също случайна величина. Нейното математическо очакване е:

                                      (5)

Дисперсията на случайната величина (4) е:

                                                           (6)

Така определената функция се нарича приведена (стандартизирана, нормирана) случайна величина. Такива величини са удобни с това, че математическото им очакване е нула, а дисперсията - единица. Таблиците и процедурите за компютърни пресмятания на статистическите разпределения като правило се дават именно за нормираните случайни величини. Самите случайни величини (ненормираните) се получават от нормираните чрез прости линейни трансформации.

Ето някои други мерки за характеристика на местоположението в статистическите разпределения:

мод, мода (mode) се нарича стойността  на аргумента, която съответствува на максималната вероятност: . Тя може да се определи чрез диференциране на вероятностната плътност по аргумента. Разпределенията с един максимум се наричат унимодални. Такива са почти всички разпределения, които представляват интерес във физиката;

медиана (median) се нарича стойността на аргумента, която съответствува на . Медианата дели дефиниционната област на вероятностната плътност на две части, във всяка от които случайната величина попада с равна вероятност (т.е. това са две равноплощни части на разпределението). За симетричните разпределения математическото очакване, модата и медианата съвпадат;

по-общо квантил (quantile) на ниво ,  се нарича стойността на аргумента , за която: . Така че медианата е квантилът на нивo 1/2. Квантилите на нивaта 1/4, 2/4, 3/4 се наричат квартили , на нивата 0.1, 0.2,...0.9 се наричат децили, а на нивата 0.01, 0.02,..., 0.99 - процентили. За често използуваните разпределения най-важните квантили са дадени в таблици и има готови изчислителни процедури за тяхното пресмятане.