7. Разпределения на няколко случайни величини

 

   7.1. Разпределения на две случайни величини

   7.2. Моменти на съвместните разпределения

   7.2.1.Свойства на моментите на съвместните разпределения

   7.3. Съвместни разпределения на повече от две случайни величини

 

7.1. Разпределения на две случайни величини

Рядко при обработката на данни се оказва възможно да се ограничим с разглеждането само на една случайна величина. Дори и да се опитваме да измерваме само една физична величина (параметър), ние се натъкваме на наличието и на други фактори, които влияят върху резултатите от измерването и които също се описват със случайни величини (типичен пример са измерванията на някакъв сигнал при наличието на фон). Адекватното описание на такива експерименти предполага едновременното изучаване на статистическите свойства на всички величини, които реално участвуват във формирането на резултатите. Затова е нужно да се изучават съвместните им вероятностни разпределения. При това възникват и някои нови свойства, които не съществуват при едномерните разпределения.

Най-простият вариант е на две случайни величини, . Ще ни интересува вероятността едновременно Както и при една случайна величина, предполагаме, че съществува функция на разпределение:

                                                                                              (1)

Във всички интересни случаи  съществува. Ако тя е диференцируема по двата си аргумента, то функцията:

                                                                                          (2)

се нарича съвместна вероятностна плътност на случайните величини . Тогава, очевидно:

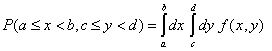                                                       (3)

Понякога възниква следният проблем: в резултат на измервания се получават множество стойности на случайните величини . По тях може приближено да се построи съвместната функция на разпределение , респективно съвместната вероятностна плътност . Ние обаче можем да се интересуваме само от поведението на величината , независимо от . Плътността на вероятностното разпределение по може да се получи чрез интегриране на  по  в цялото пространство на изменение на :

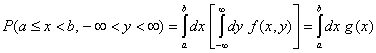                             (4)

Тук:

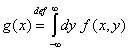                                                                                           (5)

е вероятностната плътност на случайната величина .  се нарича безусловна (маргинална) плътност на разпределението на . По подобен начин за се дефинира функцията:

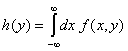                                                                                           (6)

Аналогично на понятието независими събития ние можем да определим независимостта на случайните величини  и . Именно, двете случайни величини  и се наричат независими, ако е изпълнено условието:

                                                                                            (7)

Условната вероятност също се определя с помощта на маргиналните разпределения:

                                                                                             (8)

се нарича условна плътност на вероятността за случайната величина при зададено .

За пълната вероятност е също в сила съотношението:

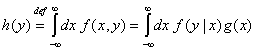                                                            (9)

За независими случайни величини:

                                                                              (10)

т.е. знанията ни за статистическото разпределение на случайната величина не увеличават информацията за разпределението на (и обратно).

7.2. Моменти на съвместните разпределения

Аналогично на едномерния случай, определяме математическото очакване на една дадена функция на случайните величини и като:

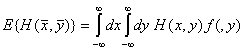                                                              (1)

a дисперсията:

                                                   (2)

Нека разгледаме функцията:

                                                                                                 (3)

Математическото очакване на тази функция се нарича -ти момент на вероятностното разпределение на случайните величини и  спрямо точката (0,0):

                                                                                                (4)

Това е нецентрален момент. По-общо се разглежда функцията:

                                                                               (5)

Нейното математическо очакване определя централните моменти на разпределението на и относно точката :

                                                                                              (6)

Особен интерес представляват моментите  спрямо точката , която е точно математическото очакване на . Младшите по ранг моменти са:

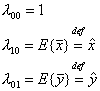                                                                                                  (7)

 

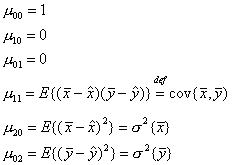                                                                 (8)

7.2.1.Свойства на моментите на съвместните разпределения

При повече от една случайна величина може да се говори и за по-сложни свойства на моментите, свързани с операциите с няколко променливи. Ето някои от тях:

                                                                            (9)

(следва непосредствено от дефиницията);

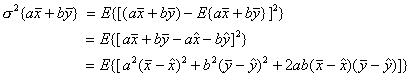                    (10)

Или:

                                       (11)

Величините , които участвуват тук, са много сходни с математическото очакване и дисперсията за едномерния случай. Що се отнася до , която се нарича ковариация на  и , тя изисква специално внимание предвид голямата й важност. От дефиницията й следва, че ковариацията е положителна, ако събитията  (респективно ) се появяват по-често едновременно, отколкото комбинациите на малки  с големи. Ковариацията е отрицателна в обратния случай, т.е. когато по-често малки (спрямо средното) стойности на  се наблюдават едновременно с големи стойности на . Накрая, , ако знанието на  не ни дава информация за стойностите на   (и обратно). Това се пояснява на следните картинки:

 

                                                                  

 

                                                                                 

                               

В много случаи е удобно вместо ковариацията да се използува величината:

                                                                                         (12)

която се нарича коефициент на корелация.

Ковариацията и коефициентът на корелация дават обобщена оценка за взаимната зависимост между случайните величини и.

За да изясним смисъла на коефициента на корелация, разглеждаме нормираните случайни величини:

                                                                                     (13)

Дисперсията на сумата е:

                                                          (14)

Тъй като за нормираните случайни величини дисперсията  е винаги 1, то:

                                                                                             (15)

По аналогичен начин за разликата се получава:

                                                                                 (16)

Но дисперсията е винаги неотрицателна, . Тогава от (15) и (16) следва:

                                                                                                (17)

В сила са следните равенства:

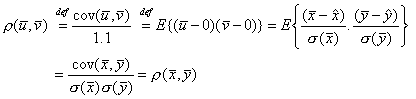                   (18)

Следователно, за всеки две случайни величини (не непременно нормирани):

                                                                                               (19)

Оттук виждаме още, че коефициентът на корелация  е и нормиран; той не зависи от мащаба по  и по  (за разлика от ковариацията).

Граничните случаи са:

а)                                 (20)

Това е функционално равенство.  То може да бъде изпълнено за всяко и всяко само ако е в сила:

                                                                                                         (21)

т.е. случайните величини и са линейно свързани и . Равенството (21) съответствува на случая на пълна линейна корелация между случайните величини ;

б) напълно аналогично при  откъдето следва:

                                                                                                                      (22)

който случай се нарича пълна линейна антикорелация.

Ако случайните величини и са независими, то

Наистина:

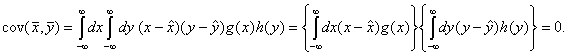
Обратното обаче не е в сила, т.е. ако ковариацията на две случайни величини е нула, те не са непременно независими.

7.3. Съвместни разпределения на повече от две случайни величини

Функцията на разпределение на  случайни величини се определя така:

                                                (1)

Вероятностната плътност се дефинира по следния начин:

                                                                          (2)

По аналогичен начин се въвеждат всички останали характеристики: маргинално разпределение, математическо очакване, дисперсия, моменти и т.н. Този случай не ни дава нищо ново, но позволява да се направи обобщено разглеждане. Именно, случайните величини могат да се разглеждат като компоненти на вектор в -мерното пространство: 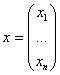. Това е вектор-стълб. Транспонираният му вектор е: . Тогава функцията на разпределение се записва така: , съответната вероятностна плътност: . Математическото очакване на една функция  добива вида:

.                                                                                (3)

Тук навсякъде  е вектор с  компоненти, интегрирането е също в -мерното пространство.

Вторите централни моменти - дисперсиите и ковариациите - могат да се обединят в една матрица с размерност , която се нарича ковариационна матрица:

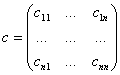                                                                                             (4)

Нейните елементи са:

                                                             (5)

Диагоналните елементи са дисперсиите (които се наричат още вариации). Матрицата  е симетрична по определение (5).

Като си дадем сметка, че множителите в (5) са компоненти на -мерен вектор, от правилото за умножение на матрици се получава:

                                                                                       (6)

Ковариационната матрица (наричана понякога вариационно-ковариационна матрица, а също и матрица на грешките) съдържа основната информация за разсейването на компонентите на един -мерен случаен вектор. По тази причина нейното пресмятане е една от главните задачи при обработката на експерименталните данни.