8. Трансформации на случайни величини. Разпространение на грешките

Стана ясно, че функцията на една случайна величина е също случайна величина: . Въпросът, който възниква често, е:  каква е вероятностната плътност , ако е известна плътността ?

Общият отговор на този въпрос е свързан с изискването за взаимна еднозначност и непрекъснатост на изображенията и и непрекъснатост на частните производни . Тогава търсената връзка е от вида:

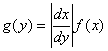                                                                                                (1)

Съотношението (1) има и многомерно обобщение. Ние няма да се занимаваме с общия случай, а ще разглеждаме само най-важния специален случай на линейни трансформации.

Линейните трансформации са най-често използуваните на практика. Причината е в простотата на действията с тях. Те например водят до линейни уравнения и системи, които много по-лесно се решават. Затова при възможност ние се стараем да преминем от нелинейни към линейни трансформации. Обикновено това се постига чрез ограничаване на Тейлъровото (Taylor) разложение на функциите до линейни членове.

Нека  и  са -мерни вектори от случайните величини и . Нека  е линейна функция на . Това означава:

                                                                                                         (2)

където а е -мерен вектор, а  матрица.

Математическото очакване на случайната величина  е:

                                                                                            (3)

Нека да видим как ще изглежда ковариационната матрица на линейната трансформация :

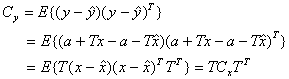                                                   (4)

(Тук помним, че матричното умножение не е комутативно!).

И така:

                                                                                                       (5)

С помощта на съотношението (5) ще формулираме едно от най-известните правила в статистиката, наречено закон за разпространение на грешките (англ. error propagation).

Нека е -вектор от известни измервания. Ние предполагаме, че:

·        средните стойности на измерванията са известни; нека те образуват вектора ;

·        средноквадратичните отклонения ("грешките") на  са също известни; те образуват ковариационната матрица .

Ние искаме да разберем каква е "грешката" на някаква функция на измерването .

Ако грешките на  са сравнително малки, то вероятностната му плътност  ще е съществено различна от нула само в неголяма околност на (тази околност е от порядъка на ). Тогава ще е в сила разложението:

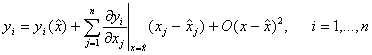                              (6)

Или, в матрична форма:

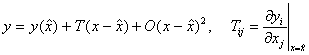                                                          (7)

Тогава, използувайки (5), получаваме:

                                                                                                       (8)

където матрицата на трансформацията  се определя от (7b). Равенството (8) изразява закона за разпространение на грешките при измерванията.

 

Казаното дотук може да се обобщи така:

·        законът за разпространение на грешките (5) е точен за линейни трансформации на случайните величини;

·        този закон може да се използува приближено и за нелинейни трансформации на случайни величини във вида (8). Това приближение е добро, когато дисперсиите на базисните случайни величини  са малки.

 

Тук трябва да се направи следната важна забележка:

Дисперсиите са, както знаем,  диагоналните елементи на съответната ковариационна матрица. Тъй като обикновено ние се интересуваме главно от дисперсиите като мярка за разсейването на резултатите от измерванията, ние сме склонни да оценяваме само . Но, забележете, че дисперсиите на трансформациите  зависят не само от дисперсиите на , но и от ковариациите . Без отчитането на ковариациите между измерванията (т.е. техните взаимни зависимости), ние можем да получим съвършено нереалистични резултати за . Само ако наблюденията  са взаимно независими помежду си, тогава  и тогава те могат да се пренебрегнат. Тогава матрицата  става диагонална и е в сила:

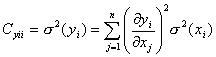                                                                     (9)

Последното съотношение е известно също като закон за разпространение на грешките и фигурира в много учебни пособия именно в този вид. Напомняме още веднъж, че (9) е валидно само при независими измервания .

Ето формули за дисперсията на някои прости функции от случайни величини, пресметнати според закона за разпространение на грешките:

Нека x₁ и х₂ са две независими случайни величини. Тогава:

 

Накратко тези правила могат да се изкажат така:

·        при събиране и изваждане се сумират дисперсиите на събираемите;

·        при умножение и деление се сумират относителните дисперсии на множителите/делителите.

 

Ако  и  не са независими, то съответните формули за дисперсията на  в случая на произведение и частно са:

 

 

С други думи, дисперсията на произведението се увеличава при положителна корелация между множителите, а дисперсията на частното намалява при положителна корелация между делителите (в сравнение с дисперсиите за независими множители/делители). При антикорелация между множителите/делителите е обратното.