9. Дискретни разпределения

9.1. Експеримент с два изхода (разпределение на Бернули)

9.3.1. Разпределението на Поасон като граничен случай на биномното разпределение

9.3.2. Директен извод на разпределението на Поасон

9.3.3. Свойства на Поасоновото разпределение

9.1. Експеримент с два изхода (разпределение на Бернули)

Най-простият възможен експеримент е този, чиято реализация води до едно от двете несъвместни събития и (например хвърляне на монета). Той е известен и като схема на Бернули (Bernouli). В такъв случай е в сила разложението:

(1)

Означаваме вероятността за "благоприятен изход" (нека за такъв приемем настъпването на събитието ) с:

(2)

Резултатът от един такъв експеримент може да се изрази чрез една случайна величина , която приема стойности 1 (0) в зависимост от това, дали е настъпило събитието . Статистическите характеристики на случайната величина са:

(3)

(4)

Разпределението на тази случайна величина изглежда така:

q p

0 1

Това е почти всичко, което може да се каже за тази най-проста случайна величина. Тя е интересна не толкова сама по себе си, колкото с това, че тя участвува в изграждането на всички важни дискретни разпределения.

9.2. Биномно разпределение

Това е вероятностното разпределение на случайна величина, описваща всевъзможните резултати от -кратното повторение на експеримента с два изхода:

(5)

където е случайна величина, описваща единичен експеримент с два изхода. Нейното разпределение ни е вече известно.

Важно допълнение тук е, че отделните единични експерименти се предполагат независими помежду си. Тогава вероятността за на брой благоприятни изходи (т.е. събитието в предишната схема) при -кратно повторение ще бъде:

(6)

Отделните членове имат такъв смисъл: е вероятността точно на брой реализации на единичния експеримент да дадат благоприятен изход, а е броят на всички възможни начини, по които може да се получат благоприятни изхода при на брой експерименти от този тип.

е вероятностното разпределение на случайната величина (5). То се нарича биномно разпределение. При него е аргумент (това е броят на благоприятните изходи, който е независимата променлива), а и са параметри (това са съответно броят реализации на единичния експеримент с два изхода и вероятността за благоприятен изход при единична реализация).

Очевидно:

(7)

така че вероятността (6) е правилно нормирана.

Математическото очакване на биномното разпределение е:

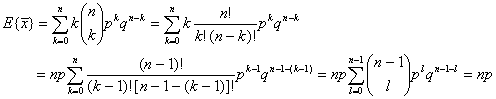(8)

Този резултат може да се пресметне и по-лесно - като използуваме вече известния ни израз за математическото очакване на единичния експеримент с два изхода (3) и правилото за математическото очакване на сума от независими случайни величини:

(9)

Съответно, за дисперсията на биномното разпределение имаме:

(10)

Като използуваме отново формулата за дисперсията на сума от независими случайни величини (ковариациите са нули), получаваме:

(11)

Ето как изглежда биномното разпределение:

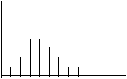
0 1 2 3 4 5

То е дефинирано само за цели неотрицателни стойности на аргумента , има максимум при и е несиметрично (с коефициент на асиметрия ).

От свойствата на биномното разпределение може да се направи едно важно наблюдение за връзката между честота и вероятност. Именно, да дефинираме честотата на събитието (благоприятният изход) в Бернулиеви опита като:

. (12)

Величината е случайна величина. Нейното математическо очакване е: (13)

а дисперсията й е:

(14)

Какво се вижда оттук?

· Първо, че математическото очакване на честотата съвпада с вероятността (която можем да предполагаме, че е неизвестна в един реален експеримент);

· Второ - с нарастването на дисперсията на честотата намалява: . Тъй като в (14) , то при фиксирано , . Следователно, с нарастването на честотата на дадено събитие все повече се доближава до вероятността за това събитие. Това свойство на честотата популярно се нарича закон за големите числа (ние обаче знаем точната формулировка на този закон: за всяко число и за всяко съществува такова , че ).

Ще споменем някои обобщения на биномното разпределение:

Полиномното разпределение е непосредствено обобщение на биномното за експерименти с краен брой изходи (повече от два). Предполагайки, че е в сила разложението:

(15)

където събитията са несъвместни, и ако

(16)

то вероятността при опита всяко от събитията да се случи пъти сe дава с:

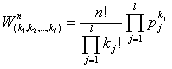(17)

(На това разпределение се подчиняват например игрите със зар).

По-сложно е т.нар. хипергеометрично разпределение, което описва вероятността от извадени топки (бели и черни) да са бели и - черни, ако и са всичките бели и черни топки и е общият брой топки в урната. Това е изваждане без повторение. В този случай последователните опити не са независими, тъй като те зависят от предисторията (така например цветът на последната топка е еднозначно известен от предишните резултати).

Тази зависимост може да се усили, ако всеки път, когато извадим топка от определен цвят, добавим в урната фиксиран брой топки от същия вид. Това е разпределението на Пойа, което има отношение към възникването на епидемии - тогава появяването на един случай увеличава вероятността за подобни заболявания.

Нека да се върнем към биномното разпределение и да разгледаме граничните случаи. Те са два:

· при фиксирана вероятност за благоприятен изход при единичния експеримент, ако броят на неговите повторения нараства неограничено, биномното разпределение клони към нормално разпределение (разпределение на Гаус (Gauss));

· ако с нарастването на вероятността за благоприятен изход намалява така, че , то биномното разпределение при клони към разпределението на Поасон (Poisson).

9.3. Разпределение на Поасон

9.3.1. Разпределението на Поасон като граничен случай на биномното разпределение

Нека означим:

(1)

Предполагаме, че е фиксирано. Тогава:

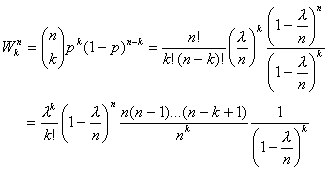(2)

При първият множител в (2) е , третият и четвъртият клонят всеки към единица, а вторият клони към експоненциална функция. Следователно:

(3)

9.3.2. Директен извод на разпределението на Поасон

Този подход се основава на конкретен физически модел и по тази причина изяснява по-добре свойствата на Поасоновото разпределение от гледна точка на физическия му смисъл.

Нека имаме радиоактивен източник с множество радиоактивни ядра, които се разпадат спонтанно. При това са в сила следните предположения:

1. Отделните събития са независими във времето (т.е. наличието на разпадане в момента не зависи от предисторията);

2. Вероятността за отделно събитие (разпадане) за малък интервал от време е пропорционална на дължината на интервала: (4)

3. Вероятността за повече от едно събитие (разпадане) в малък интервал от време е 0.

Ние търсим вероятността в интервала време да се случат на брой разпадания. За целта ще образуваме и и ще получим диференциално уравнение за при .

Първо търсим . За да има нула разпадания в интервала трябва да няма разпадания както в интервала , така и в интервала . Съгласно първото условие тези събития са независими, следователно:

(5)

(напомняме, че e вероятността за неразпадане в интервал с дължина ). Следователно:

(6)

При :

(7)

Общото решение на (7) е:

(8)

където е произволна константа.

За да се определи стойността на , е необходимо едно начално условие. Логично е да предпоставим:

(9)

т.е. вероятността за неразпадане в интервал с дължина нула е равна на тази на достоверното събитие. Тогава, окончателно:

(10)

Това всъщност е известният закон за радиоактивното разпадане.

Нека сега , т.е. търсим вероятността за точно едно разпадане в интервала . Има две възможности: едно разпадане в и нула разпадания в или обратното. Тези сложни събития са несъвместни, така че общата вероятност е сума от техните вероятности:

(11)

Следователно:

(12)

Това уравнение има решение:

(13)

Това е вероятността за точно едно разпадане в интервала .

Горното разглеждане е напълно приложимо и за общия случай ():

(14)

тъй като според третото предположение на модела повече от едно разпадане в интервала не е възможно. Следователно:

(15)

При , това диференциално уравнение има решение:

(16)

което е всъщност Поасоновото разпределение.

Разглеждайки тази картина статично, (т.е. като анализираме броя на наблюдаваните разпадания за даден фиксиран интервал от време), ние виждаме, че има смисъл на среден брой разпадания за дадения интервал, а e вероятността да получим на брой разпадания, ако средният им брой е. Оттук се вижда и физическият смисъл на параметъра m; това е средната скорост на разпадане на радиоактивните ядра.

9.3.3. Свойства на Поасоновото разпределение

Разпределението на Поасон (3) е дефинирано за всички цели неотрицателни стойности на своя аргумент . То зависи от един параметър l, който е реално неотрицателно число.

Нормировка:

(17)

откъдето се вижда, че разпределението, дефинирано чрез (3), е нормирано коректно.

Средна стойност:

(18)

Дисперсия:

(19)

Развиваме израза за квадрата в скобите. Вторият и третият членове са от познат вид. Първият е:

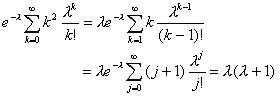(20)

Следователно:

(21)

Забележка: Дисперсията може да се пресметне и като се използува резултата (9.11), за дисперсията на биномното разпределение, тъй като Поасоновото разпределение е всъщност един негов частен случай. Именно:

(22)

Асиметрия:

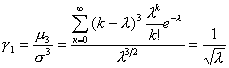(23)

От написаното се вижда, че:

· параметърът l действително има смисъл на средна стойност, което оправдава названието му при втория подход (среден брой разпадания);

· дисперсията на Поасоновото разпределение е равна на средната му стойност;

· асиметрията на Поасоновото разпределение е винаги положителна; с увеличаването на l тя намалява, т.е. разпределението става по-симетрично.

Поасоновото разпределение се получава от биномното при голям брой повторения на експеримент с малка вероятност за благоприятен изход; поради това то е известно още като разпределение на редките събития.

Радиоактивното разпадане е вероятно най-известният пример за явление, подчиняващо се на Поасоновото разпределение. Има обаче още много други такива явления:

· броят на научните открития, направени неколкократно при независими изследвания;

· броят на звездите в определен ъглов диапазон на небесния свод,

· и др.