Упражнение № 1

 

МЕТОДИ ЗА АНАЛИЗ И КОНТРОЛ С ПРЕМИНАЛИ БЕТА-ЛЪЧИ

 

            Преминали бета-лъчи

            Броят на преминалите през определена дебелина частици зависи от вида и енергията на частиците. Известно е, че броят на моноенергетичните алфа-частици остава неизменен до известна дебелина, след което бързо намалява,като неопределеността на пробега е до 2-3 % от общия пробег (виж. крива 1) на Фиг.1).

 

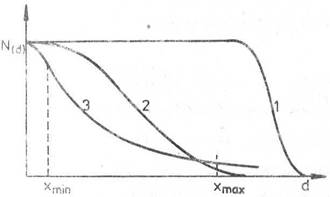
Фиг.1. Зависимост на броя преминали частици от дебелината на материала.

 

            Експериментите с моноенергетични електрони обаче показват, че неопределеността в пробега на електроните е твърде значителна - зависимостта на броя на електроните от дебелината (крива 2) много малко прилича на кривата за алфа-частици. За електрони, получени от бета-разпад, зависимостта на броя преминали електрони от дебелината (крива 3) е функция, напълно различна от горните случаи. Експериментален резултат е, че в областта на средни дебелини на поглътителя тази зависимост е експоненциална функция:

,       (1)

където d е дебелината на поглътителя, а m е коефициентът на отслабване (линеен, ако дебелината е в линейни единици, и масов m/r , ако дебелината е изразена в масови единици dr).

            Този емпиричен закон е приблизителен. На Фиг.2 са дадени минималните и максималните дебелини в зависимост от енергията на бета-прехода, за които законът е валиден. Извън тези дебелини на слоя вещество отклонението от експоненциалната зависимост може да достигне 10 и повече процента. За големи дебелини зависимостта преминава в линейна функция. На фигурата са показани минималните и максималните дебелини, в границите на които законът на отслабване е приблизително експоненциален.

 

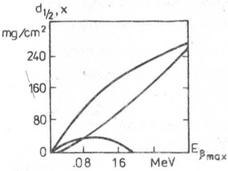
Фиг. 2. Зависимост на слоя на полуотслабване на преминалите бета-частици от максималната енергия на бета-спектъра.

 

            Преминаващите през веществото електрони си взаимодействуват главно с електроните от средата. Поради това броят на електроните, преминали през проба с определена дебелина, зависи само от броя на електроните в пробата на квадратен сантиметър. Броят на електроните на 1 cм от пробата се определя от:

 

,         (2)

където N_A е числото на Авогадро, А е масовото число на елемента на пробата, Z е атомният номер на елемента на пробата, а m = dr е дебелината на пробата в g/cм².

            Съотношението (2) дава възможност да се градуират прибори за измерване на дебелини. Резултатите от градуировката с един материал с определени Z₁/А₁ могат да се приложат за друг материал със Z₂/А₂ , като дебелините по абсцисата за втория материал се умножат със (Z₁/А₁)/(Z₂/А₂). За леки елементи ( до Ca ) отношението Z/А е 1/2 и поради това не е нужна корекция.

            Съществуват емпирични формули за масовия коефициент на отслабване (в cм²/g):

 

,         (3)

където Е_m е максималната енергия на бета-спектъра в MeV.

 

 

 

Упражнение

Определяне на дебелините на тънки лентови материали с преминали бета-лъчи

 

            Определянето на масовите дебелини на тънки лентови материали се основава на приблизително експоненциалния закон на поглъщане на бета-лъчите от веществото.

 

Задача:

Да се измерят масовите дебелини на хартия и метално фолио.

 

Апаратура:

 

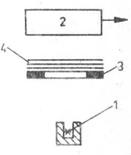
Фиг. 3. Опитна постановка за измерване на дебелини на лентови материали.

 

            Източник на бета-лъчи ¹⁴⁷Pm (Е_max=224,5 keV, Е_b = 62 keV , активност на източника: А»10 mCi (А»37 kBq), детектор - СБТ-10, преброител.

            Геометрията на опита е показана на Фиг.3, където 1 е източник+kонтейнер, 2 е детектор, 3 е държател, а - 4 - лентов материал.

 

            Изпълнение:

 

            1. Построяване на калибровъчна крива с хартиени еталони с известна дебелина. Използува се тънка хартия и за всяко ново измерване се добавя по един слой.

            2. Определяне на експерименталния масов коефициент на поглъщане за този нуклид.

            За целта е необходимо да се построи кривата на отслабване на бета-частиците в полулогаритмичен мащаб: по абсцисната ос се нанася в линеен мащаб дебелината на поглътителя x_i в масови единици, а по ординатната ос се нанася , където  е интензитетът на регистрираното бета-лъчение след преминаването му през слой с дебелина x_i, а N_b е фонът на установката (измерва се като се закрие източникът). Наклонът на получената права линия (в правия участък) дава стойността на m/r.

            Сравнете експерименталната стойност на m/r с изчислената по една от емпиричните формули (3) или от графиката на Фиг.2, където е дадена зависимостта на слоя на полуотслабване от енергията. Връзката между m/r и слоя на полуотслабване  е .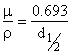

            Колко сантиметра е слоят на полуотслабване във въздух, като се знае, че плътността на въздуха е приблизително равна на 1,3 mg/cm³? Какви изводи трябва да се направят за геометрията на опита ?

            3. Измерване на дебелините на неизвестни проби и оценка на грешката при измерването.

 

Забележка

            Обработката на експерименталните резултати може да се направи с помощта на програмата MLS2.