Упражнение № 2
МЕТОДИ
ЗА АНАЛИЗ И КОНТРОЛ С ОБРАТНО РАЗСЕЯНИ БЕТА-ЛЪЧИ
Обратно разсеяни бета-лъчи
1. Основни зависимости при разсейване на електрони
Точна количествена теория за явлението обратно разсейване на бета-лъчи няма. За приблизителни количествени и качествени оценки се използува емпиричен израз за зависимостта на интензитета на обратно разсеяните бета-лъчи (при нормално падане и отражение) от атомния номер Z на материала:
, (1)
където коефициентът a зависи от геометрията на опита, а коефициентът b (b=0,6-0,8) зависи от гладкостта на повърхността на материала.
Тази зависимост определя и областта на приложение на метода. С обратно разсеяни бета-лъчи могат да се мерят покрития тогава, когато атомните номера на покритието и подложката силно се различават - например покрития от тежки метали върху желязо, мед, месинг, а също така и лакови покрития върху метали.
Интензитетът на обратно разсеяните електрони зависи слабо от енергията им в областта до 1 MeV , след което бързо започва да намалява.
Горните две зависимости са илюстрирани с експериментални данни, показани на Фиг.1.
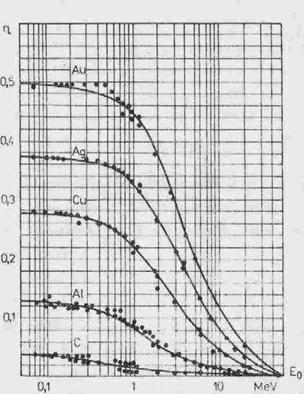
Фиг. 1. Зависимост на експериментално измерения
коефициент на отражение на електрони от енергията, за елементи с различен
атомен номер.
При отражение на електрони от повърхност съществува емпирична зависимост, която наподобява закона за равенство на ъглите на падане и отражение в оптиката. Най-голям брой електрони действително се разсейва под ъгъл, равен на ъгъла на падането, но има и значителен брой електрони, разсеяни под други ъгли (Фиг.2).
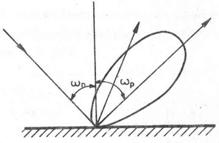
Фиг. 2. Разсейване на електрони от повърхност
При постоянен ъгъл
на падане 
, интензитетът на
разсеяните електрони зависи от ъгъла
на разсейване 
, като ако
е в равнината на
падане, интензитетът е приблизително пропорционален на 
. Същата приблизителна зависимост
съществува и за ъгли на разсейване,
които не лежат в равнината на падане. Тази ъглова зависимост на разсеяното лъчение
позволява да се конструират прибори за измерване
на грапавостта на повърхнини, тъй като с увеличаване
на грапавостта изотропията на разсеяното лъчение постепенно нараства (фиг. 3).
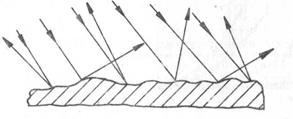
Фиг.3. Разсейване на електрони от неравна повърхност
С увеличаване на ъгъла на падане (съответно и на отражение), интензитетът на разсеяното лъчение расте, като постепенно намалява зависимостта от атомния номер (Фиг.4).
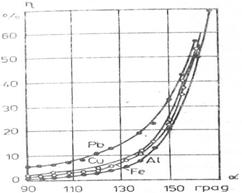
Фиг. 4. Зависимост на коефициента на отражение за различни елементи от сумата a на ъгъла на падане и ъгъла на отражение
Този експериментален резултат показва, че най-добрата геометрия за определяне на дебелини на покрития (различимост по Z) е при нормално падане и отражение.
Зависимостта на интензитета на обратно разсеяните
бета-лъчи от дебелината d се пресмята по следния
начин. При преминаване на слой с дебелина x, до елементарния слой dx достигат
електрони
където 
е броят на
падащите електрони на 1 cm2 за 1 s , 
е масовият
коефициент на отслабване. От слоя dx се разсейват 
електрони.
При преминаване отново през слоя
с дебелина x бета- лъчите намаляват отново с множител 
. След интегриране
по x от 0 до 
се получава
(2)
По-точен е емпиричният израз 
, т.е. в експонентата
присъствува множител 2,5 вместо 2. Това се обяснява с факта, че при
преминаването си през веществото електронът губи енергия, поради което обратно разсеяните
електрони са с по-ниска енергия, отколкото падащите на повърхността. По-малката енергия означава по-голям коефициент 
. Приблизително може
да се приеме,
че =1,5
. Поради това
в показателя на степента се появява
множителят 2,5 (Съществуват и други приближения).
Упражнение
ИЗМЕРВАНЕ НА СЪДЪРЖАНИЕТО НА ТЕЖКИ ЕЛЕМЕНТИ В
ПРАХООБРАЗНИ ПРОБИ С ОБРАТНО РАЗСЕЯНИ БЕТА-ЛЪЧИ
При разсейване на бета-лъчи от двукомпонентна смес изразът за интензитета на обратно разсеяните електрони е сума от разсейването от двата елемента поотделно със съответния коефициент
, (1)
където Z1 и Z2 са атомните номера на двата елемента, C1 и C2 са концентрациите на двата елемента (C1= d1/(d1 + d2 ), C2 = d2/(d1+ d2), C1+C2= 1), d1 и d2 са масовите дебелини на двата елемента в пробата и d=d1+d2 е масовата дебелина на цялата проба. Като имаме предвид, че m1/r1=m2/r2 (масовите коефициенти на поглъщане m/r за два различни елемента са еднакви с точност до Z/A, където А е масовото число на елемента), то за израза (1) получаваме:
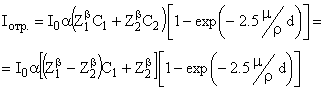(2)
Да разгледаме два крайни случая :
а) за “дебели”
проби 
; 
и тогава:
, (3)
т.е. интензитетът на
обратно разсеяните електрони зависи линейно от концентрацията,
като при 
интензитетът расте с увеличаването на 
и съответно намалява
с нарастването на 
при
.
б)
за “тънки”
проби 
; 
и тогава:
. (4)
За големи разлики в атомните номера Z1>> Z2, теглото на пробата d=d1+d2 зависи главно от теглото на единия елемент, т.е. d1+d2»d1 и d1»C1, тогава:
. (5)
Горната зависимост показва, че за “тънки” проби интензитетът на обратно разсеяните електрони зависи квадратично от концентрацията C1. При квадратична зависимост методът е по-чувствителен за малки концентрации. За всички междинни случаи интензитетът на обратно разсеяните електрони зависи от концентрацията със степенен показател между 1 и 2.
Задача
Да се измери концентрацията на PbCO3 в прахообразни проби от лек пълнител ( варовик ) .
Апаратура
Източник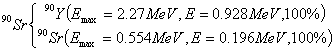 
Детектор СБТ-10, преброител.
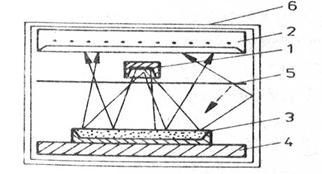
Фиг. 5. Схема на опитната постановка
за измерване на концентрацията на PbCO3
Геометрията на опита е показана на Фиг. 5, където 1 е радиоактивен източник (90Sr ), 2 - детектор СБТ-10, 3 - изследвано вещество, 4 - пластмасов държател, 5 - алуминиев филтър, 6 - камера. Стените на камерата са от алуминий. Алуминиевият филтър задържа или отразява разсеяните под голям ъгъл електрони.
Изпълнение
1. Построяване на калибровъчна крива за проби с известна концентрация. Пробите трябва да бъдат приготвяни по еднакъв начин. Препоръчва се от чашката с дадена концентрация да се насипва в алуминиева кювета достатъчно количество вещество (с връх), след което с линийка, която се плъзга по ръбовете на кюветата, се отнема излишното количество.
2. Измерване на неизвестни проби и оценка на грешката.
Забележка
Обработката на експерименталните резултати може да се направи
с помощта на програмата MLS3.