Класически вероятностен модел

Интуитивно понятие за вероятност. Вероятността като честота

Както казахме, експериментът представлява съвкупност от условия (т.е. предписания, свързани с условията на наблюдение), чието изпълнение гарантира получаването на някакъв резултат/резултати. Те се наричат още изходи от експеримента или събития. Ако изходите от даден експеримент при различни негови реализации са различни, ние говорим за случайни събития.

Оказва се, че не е възможно да се предскаже дали дадено събитие ще се сбъдне или не при следващия опит. При многократно провеждане на един и същ експеримент обаче се наблюдават определени закономерности, които като правило стават все по-отчетливи с увеличаването на броя на опитите. Поради това в стохастиката се разглеждат само случайни събития, които могат да се възпроизвеждат многократно, т.е. имат масов характер.

Класическите примери за случайни събития са добре известни. Ето кратка таблица:

експеримент	случайно събитие
хвърляне на монета	попадане на лице/герб
хвърляне на зарове	получаване на определено число
изтегляне на числа от Тото2	получаване на печеливша комбинация

Ако при експеримента събитието се е сбъднало пъти, числото се нарича относителна честота (понякога само честота) на сбъдване на събитието .

Ясно е, че винаги е в сила:

(1)

За да се определи вероятността за настъпване на дадено събитие могат да се извършат голям брой опити при еднакви условия. За всяка редица от опити може да се определи относителната честота за сбъдване на . При голям брой опити стойностите на тази честота се стабилизират около някаква стойност, т.е. редицата от числа изглежда да е сходяща. Ние не можем да установим сходимостта на редицата от относителни честоти опитно, тъй като не сме в състояние да извършим безкраен брой експерименти. Естествено е обаче да направим такова предположение като обобщение на натрупания опит и да дефинираме вероятността като граница:

(2)

Така се достига до статистическото (наричано още честотно или класическо) определение за вероятността. Най-общо казано, вероятността за дадено събитие е количествена мярка за възможността събитието да настъпи.

В някои случаи е възможно вероятността за дадено събитие да бъде определена чрез пресмятане, без да се извършват голям брой експерименти. Необходимо условие за това е наличието на (или предположението за) равна възможност за сбъдване на различните изходи от експеримента. Такива експерименти се наричат още експерименти с равновероятни изходи.

Примери за експерименти с краен брой равновероятни изходи бяха вече посочени (хвърляне на монета, зарове, изтегляне на топки от урна или на игрални карти от колода). В такива случаи общият брой изходи и благоприятните изходи просто могат да се изброят.

Геометрична вероятност

Има задачи, при които изходите са също равновероятни, но не са краен брой. Така е например при така наречените геометрични вероятности.

Най-простият пример за геометрична вероятност е следният мислен експеримент: Нека върху отсечката напосоки се хвърля една точка. Интересуваме се каква е вероятността за това, тя да попадне в интервала ?

В този прост случай отговорът изглежда очевиден. Доколкото вероятността да попаднем в интервала не зависи от това, къде се намира той спрямо основния интервал , то търсената вероятност ще бъде: , т.е. ще зависи само от отношението на дължините на интервалите. Ясно е, че този извод изцяло се обуславя от интерпретацията на условията на експеримента, съгласно които точката се хвърля “напосоки” върху интервала.

В този случай броят на елементарните изходи е безкраен, дори е континуум. В такива случаи вероятността е удобно да се пресмята чрез така наречената вероятностна плътност , която се определя като вероятност за попадане върху някакъв елементарен интервал с дължина : . Тогава вероятността за попадане в интервал с крайна дължина е: 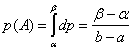, т.е. получава се резултатът, който вече знаем. Този подход (с интегриране на вероятностната плътност) обаче е много по-мощен и позволява да се решават много по-сложни задачи.

Ето още един пример за геометрична вероятност: Във вътрешността на квадрат със страна се избира по случаен начин точка. Каква е вероятността разстоянието от точката до центъра на квадрата да не е по-голямо от ?

Нека означим с търсеното събитие (точката да е на разстояние до центъра на кръга, не по-голямо от . Очевидно събитието настъпва тогава и само тогава, когато точката лежи в кръг с радиус около центъра на квадрата. Тогава вероятността да настъпи ще е отношението на площта на кръга (т.е. “благоприятните изходи”) към площта на квадрата (“всичките изходи”). Или: .

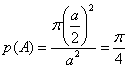Комбинаторна вероятност. Правила за броене

Тук ще разгледаме по-подробно комбинаторната вероятност предвид голямата й практическа важност. Припомняме, че условията за приложимост на комбинаторната вероятност са:

броят на елементарните изходи от експеримента да е краен;

всички елементарни изходи да са “равновъзможни” в смисъл, че няма основания да очакваме, че някой от тях ще настъпи по-често от другите. (Често понятията “равновъзможни” и равновероятни се използуват като еквивалентни).

Типични примери за приложимост на комбинаторната вероятност са хазартните игри, където се вземат специални мерки за осигуряване “равновъзможност” на изходите (балансиране на заровете и рулетките, еднаквост на гърбовете на картите за игра и пр.). В тези случаи вероятността за дадено събитие може да се дефинира просто като относителна честота, разделяйки броя на “равновъзможните” начини за настъпване на търсеното събитие към броя на всички “равновъзможни” изходи на експеримента.

Правилата за пресмятане на комбинаторната вероятност са известни още като правила за броене. Те указват начина, по който да се определи броят на изходите от експеримента и броят на благоприятните изходи.

В общия случай предполагаме, че броят на всички възможни изходи е , а броят на реализациите на експеримента е . Аналогията с изваждане на топки от урна тук е много полезна. Множеството от всички възможни изходи се нарича популация, а това от резултатите от експеримента – извадка с обем .

Обемът на популацията е свойство на условията на експеримента и за всеки конкретен експеримент е фиксирано число. Напротив, броят на реализациите на експеримента зависи от (търпението на) експериментатора и може да е произволен.

В зависимост от условията на експеримента извадката може да бъде:

с повторение – когато резултатът от експеримента може да бъде получаван неограничен брой пъти (изтеглената топка се връща в урната);

без повторение – когато даден изход може да бъде реализиран само веднъж (т.е. изтеглена топка не се връща повече в урната).

Пример за извадка с повторение е хвърлянето на зарове, а за извадка без повторение – изтеглянето на числата на Тото2.

Очевидно при извадката с повторение нейният обем е неограничен, т.е. може да е и по-голямо от , докато при извадка без повторение винаги .

Друга характерна особеност на извадките е тяхната наредба. Една извадка се нарича:

наредена, ако за експеримента е от значение редът на последователно получаване на резултатите;

ненаредена – в противния случай.

Пример за наредена извадка е съобщаването на числата от Тото2 в последователността, в която са изтеглени, тъй като всяка от топките в урната има свой номер. Напротив, ако всички топки са еднакви (бели), всяка извадка би била ненаредена.

Понятията, изброени по-горе, имат важни аналогии в статистическата физика, където се говори за ансамбли (т.е. популации) от различими или от неразличими частици (това е аналогията на наредени и ненаредени извадки съответно), или пък за системи, подчиняващи се на принципа на Паули, където броят на частиците, които могат едновременно да бъдат в едно и също състояние е ограничен (това е аналогия на извадка без връщане).

Преминаваме към правилата за броене в зависимост от типовете извадки.

Наредена извадка без повторение

Първият елемент от извадката може да бъде получен без ограничения измежду всичките елемента на популацията. Вторият елемент може да бъде “равновъзможно” избран между оставащите елемента. Това означава, че два определени елемента могат да бъдат получени по начина. Този процес може да се обобщи по очевиден начин. Така излиза, че елемента могат да се получат измежду популация с обем по начина. Числата се наричат вариации от елемента ти клас. Очевидно:

(3)

Тук, разбира се, и си спомняме, че по дефиниция .

При имаме . В този случай различните изходи представляват само размествания на всички елементи на популацията на различни места. Числатасе наричат пермутации на елемента.

Пример. От колода от 52 карти изтегляме последователно три. Каква е вероятността последната изтеглена карта да е дама?

Решение. Всичките начини, по които се получават три карти от 52 са 52.51.50=132600. За да преброим благоприятните изходи, предполагаме, че резултатът е налице, т.е. последната изтеглена карта е дама. Нека за конкретност тя е дама спатия. В такъв случай дамата спатия не е била изтеглена нито първия, нито втория път. Следователно, популацията за първото теглене се редуцира до 51 карти (всички без дамата спатия). От тази популация броят на възможните изходи за първите две тегления е 51.50=2550. По-нататък съобразяваме, че благоприятен изход се получава също ако третата изтеглена карта е друга дама (каро, купа или пика). Очевидно в тези случаи броят на изходите за първите две тегления е същия, т.е. търсената вероятност е:

. Сигурно трябва да се досетим, че този резултат може да се получи и по-просто. Как?

Наредена извадка с повторение

Първият елемент от извадката може да бъде равновъзможно получен измежду всичките елемента. След това, за разлика от предишното разглеждане, го връщаме. При това вторият елемент се изтегля измежду популация със същия размер. Оттук следва, че първият и вторият елементи могат да бъдат изтеглени общо по начина. Тази аналогия може да се продължи неограничено, т.е. може да бъде и по-голямо от . Общият брой изходи е:

(4)

Пример. Колко са различните четирибуквени думи, които могат да бъдат образувани от буквите на българската азбука?

Решение. Всяка от буквите може без ограничение да стои на всяка от четирите позиции на думата (ако се абстрахираме за момент от правилата на българската граматика!). Нашите букви са 30, така че броят на различните думи е:

Ненаредена извадка без повторение

Означаваме търсения брой на ненаредените извадки без повторение с . В раздел 1.3.1. ние получихме броя на наредените извадки без повторение (вариациите ). Явно броят на ненаредените извадки ще е по-малък от броя на наредените (защото поредиците от вида ще са неразличими в нашия случай (подредбата на елементите не играе роля). По-точно, ще е толкова пъти по-малко от , по колкото начина може да се нареди една ненаредена извадка с обем . Този брой обаче е известен – това е броят на пермутациите от елемента или . Окончателно:

(5)

Последният символ е известният биномен коефициент. Числата се наричат комбинации от елемента ти клас.

Класическият пример в този случай е за пресмятане на броя на комбинациите, които трябва да попълни играч на Тото2, за да улучи със сигурност максималната печалба. Този брой съответствува на ненаредена извадка от 6 числа без повторение. Популацията е от всичко 49 числа. Така че резултатът е:

Разбира се, заедно с максималната печалба от 6 познати числа при това ще се получат всички по-малки печалби.

Ненаредена извадка с повторение

Броят на различните начини, по които може да се получи ненаредена извадка с обем измежду елемента с повторение, е:

(6)

Този резултат привеждаме без доказателство.

Исторически бележки

Развитието на стохастиката и оформянето й като математична дисциплина е тясно свързано с хазартните игри и по-специално с осъзнаването на факта, че резултатите от тях не могат да се опишат в рамките на известните дотогава класически раздели на математиката (алгебра, анализ, геометрия). Класическата теория на вероятностите е развита през XVII-XIX век по пътя на формализацията на интуитивните представи за вероятност, за които вече стана дума. За основатели на математичната теория на вероятностите се смятат Пиер Ферма (1601-1665) и Блез Паскал (1623-1662), които през 1654г. установяват някои от основните й положения. Въз основа на тях Христиан Хюйгенс (1629-1695) публикува през 1657г. първия трактат по теория на вероятностите, озаглавен “За пресмятанията при хазартните игри”. За научната общност още тогава е било ясно, че резултатите на Ферма, Паскал и Хюйгенс далеч не се отнасят само до въпросите на хазартните игри, а полагат основите на нова дълбока математична теория. Следващата важна крачка принадлежи на Якоб Бернули (1654-1705) в неговия труд “Изкуството на предположението” (“Ars conjectandi”). Фундаменталните трудове на Авраам де Моавр (1667-1754) “Учение за случая” и особено на Пиер Симон Лаплас (1749-1827) “Аналитична теория на вероятносите” придават до голяма степен завършен вид на класическата теория на вероятностите.

След епохата на Лаплас интересът към теорията на вероятностите е отслабнал значително до степен да бъде поставена под съмнение принадлежността й към математическите дисциплини. Главната причина за това е несигурната в логическо отношение основа на теорията. Такова е самото честотно определение за вероятност, което се основава на свой ред на понятието "равновероятен изход", т.е. получава се логически порочна схема. Освен това широк клас случайни явления остават необясними в рамките на честотното определение. Такива са например геометричните вероятности, както и всички други експерименти с изходи, които образуват непрекъснато множество (интервал, област и др.).

По-нататъшното развитие на теорията на вероятностите е свързано с имената на Пафнутий Львович Чебышев (1821-1894), Андрей Андреевич Марков (1856-1922) и др. Съвременен вид този дял от математиката е получил през XX век, когато е създадена аксиоматичната теория на вероятностите на Андрей Николаевич Колмогоров (1903-1987) ("Основни понятия на теорията на вероятностите", 1933).