Аксиоматична теория на вероятностите

Едно от големите ограничения на разгледаната дотук класическа вероятностна схема е изискването за равновъзможност на отделните изходи от експеримента (другият недостатък е от теоретичен порядък и е свързан с неудовлетворителния начин за дефиниране на вероятността като граница на честотата при очевидната невъзможност тази граница да бъде определена). В съвременната теория на вероятностите тези трудности се преодоляват и тя се изгражда дедуктивно, т.е. тръгвайки от определен малък брой  начални предположения, които се приемат без доказателство (т.е. аксиоми). В тази глава ние ще дадем представа за основите на тази теория.

Пространство на елементарните събития. Алгебра на събитията

В общата теоретико-вероятностна схема се предполага, че за всеки експеримент със случаен изход трябва да бъдат указани всички възможни елементарни изходи, които се характеризират със следното основно свойство: при всяка реализация на експеримента е възможен един и само един от тези изходи. Всеки такъв изход се нарича още елементарно събитие; то е елементарно в смисъл, че не може да бъде разложено на “още по-елементарни”.

Множеството от всички елементарни събития се нарича пространство на елементарните събития  за дадения експеримент. Отделните елементарни събития се наричат точки в пространството на елементарните събития.

Всеки резултат от експеримента пък се нарича “събитие” (). За всяко елементарно събитие може да се определи дали неговото настъпване води непременно до настъпването и на събитието  (бележи се  и се казва “ влече ”). По този начин, всяко конкретно събитие напълно се характеризира с множеството от всички елементарни събития, при които то настъпва. (Например, при хвърлянето на зар събитието “получаване на нечетно число” е сложно; то е съвкупност от събитията “1”, “3” и “5”, които са вече елементарни). Обратно, всяко множество от точки  може да се разглежда като събитие , което или настъпва, или не в зависимост от това дали конкретният изход от експеримента  ще бъде точка от или не. По този начин на всяко събитие  се съпоставя едно подмножество  и те могат да се разглеждат като еквивалентни.

Сега пристъпваме към формулировката на естествените операции над събитията и на техните аналози от теорията на множествата. Съвкупността от тези операции характеризира алгебричната структура на пространството на елементарните събития.

1. Ако събитието настъпва винаги, когато настъпва събитието , казваме, че е следствие от и пишем: или . В термините на теорията на множествата това означава, че всяка точка от се съдържа в или че е подмножество на .

2. Ако и , то събитията и настъпват винаги едновременно. В такъв случай пишем  и казваме, че събитията и  са еквивалентни; при това множествата и съвпадат.

3. Събитието, което настъпва тогава и само тогава, когато не настъпва , се нарича противоположно на и се означава с . Множеството се състои от всички точки на , които не принадлежат на и се нарича допълнение на .

4. Ако събитието не съдържа нито едно елементарно събитие, то се нарича невъзможно събитие и се бележи с Æ. Противоположно на Æ е очевидно събитието  , което се случва винаги. То се нарича достоверно събитие. Може да се каже още, че Æ е празното подмножество на .

5. Събитието , настъпващо тогава и само тогава, когато настъпват събитията и , се нарича тяхно произведение или сечение на и  и се бележи с или . Множеството  се състои от всички точки, които принадлежат както на , така и на , и също се нарича сечение на множествата и .

6. Събитията и  се наричат несъвместими, ако тяхното едновременно настъпване е невъзможно, т.е. ако . На несъвместимите събития съответствуват непресичащи се (т.е. нямащи общи точки) множества.

7. Събитието , състоящо се в настъпването на поне едно от събитията и , се нарича тяхна сума или обединение на и. За обединението се използува символичния запис  . Ако, може да се напише още . От гледна точка на теорията на множествата, множеството  се състои от всички точки, които принадлежат поне на едно от множестватаи .

Допълнение: Обединението и сечението се дефинират за произволен брой събития. Например, събитието  настъпва тогава, когато настъпи поне едно от събитията . Аналогично се дефинира и сечение на повече от две събития. Операциите обединение и сечение са комутативни:

и асоциативни:

8. Събитието , състоящо се в това, че настъпва събитие и едновременно с това не настъпва , се нарича разлика на събитията и  и се бележи с . Изказано чрез термините на теорията на множествата, множеството  се състои от всички точки, които принадлежат на множеството и не принадлежат на. То се нарича също разлика на множествата и .

Изброените 8 основни свойства на операциите над събитията дават възможност да бъдат извършвани и други операции. Ще отбележим специално взаимната дистрибутивност на операциите обединение () и сечение ():

В сила са и следните равенства, известни като закони на де Морган:

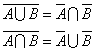
Всяко множество (клас) от събития в , за което:

1) ;

2) за всяко събитие , е в сила и ;

3) за всеки две събития , следва, че и ,

се нарича алгебра на събитията в пространството .

Пример. Да се опитаме да определим алгебрата на събитията при хвърляне на зар. За простота ще номерираме събитията “попадане на числото 1” с 1 и т.н.

Пространството на елементарните събития се състои от 6 елементарни събития: . Към алгебрата се отнася преди всичко (винаги!) празното множество . След това трябва да добавим единичните събития 1,...,6 (6 на брой), обединенията по двойки от типа ,... (броят на различните двойки е 15), обединенията по тройки от типа  (на брой 20), после обединенията по четворки (15), по петици (6) и накрая обединението на всички 6 елементарни събития  (то е само едно). Общият брой на елементите от алгебрата (класа ) e . По-общо, за всяко пространство , състоящо се от елементарни събития, се състои от събития. Често се казва, че алгебрата е множеството от всички подмножества на основното пространство. Това е вярно твърдение.

Понятията пространство на елементарните събития и алгебрата на събитията дават възможност да бъдат въведени аксиомите на вероятността.

Аксиоми на вероятността

Вероятността може да се въведе и аксиоматично (Колмогоров) чрез един минимален брой аксиоми. Тук ние ще ги скицираме:

1. (неотрицателност): На всяко събитие  съответствува неотрицателно число, което се нарича негова вероятност: ;

2. (нормировка): Достоверното събитие  има вероятност единица: ;

3. (адитивност): Ако събитията  и  са несъвместими (не могат да се случат едновременно), то вероятността за настъпване на  или  е: ;

4. (непрекъснатост): За всяка редица от вложени събития, клоняща към празното множество, редицата от техните вероятности е сходяща с граница 0: .

От тези аксиоми лесно се получават някои важни следствия:

· .

·

· За всеки две събития  и  е в сила:

·  (неравенство на Бул)

· Ако , то .

Условна вероятност

До понятието условна вероятност се достига винаги, когато се интересуваме от вероятността за настъпване на някакво събитие  и имаме някаква допълнителна информация от експеримента, която се изразява в това, че някакво друго събитие  вече е настъпило. Тогава, ако , то условната вероятност да се случи събитието  при условие, че вече е настъпило събитието , се определя така:

Оттук:

.                                                                           (1)

В тези изрази  е сечението на събитието  със събитието .

Установява се, че така дефинираната величина удовлетворява всички свойства на вероятността (както е определена чрез аксиомите на Колмогоров), т.е. условната вероятност е вероятност.

Изразът (1) се обобщава за повече от две събития по следния начин: Ако имаме  събития , за които , то е в сила:

. Този израз е известен като правило за умножение на условната вероятност.

Друго следствие е формулата за пълната вероятност за дадено събитие:

Нека даден експеримент води към някое от следните несъвместими събития:

Тогава вероятността да се осъществи кое да е събитие  е:

.

Стохастична независимост

Разгледаното в предния раздел понятие условна вероятност е мярка за влиянието на едно събитие  върху друго . В практиката има много случаи, когато е налице такова влияние, макар че то може да бъде понякога много сложно (например влияе ли слънчевата активност върху количеството на валежите?). Има обаче случаи, когато настъпването (или ненастъпването) на едно събитие не зависи и не влияе на настъпването (ненастъпването) на друго събитие. В такива случаи ние казваме, че двете събития са независими едно от друго. По-точната дефиниция на независимите събития е свързана с едно основно тяхно свойство: две събития  и  се наричат независими помежду си, ако . Това определение лесно се обобщава за повече независими събития.

Връзката между понятията независимост и условна вероятност се установява чрез следната теорема: Ако , то необходимото и достатъчно условие събитията  и да са независими е , т.е. условната вероятност за настъпване на при условие, че е настъпило  да е равна на самата (безусловна) вероятност , или с други думи да не зависи от . Този резултат се установява лесно:

 (достатъчност). Докажете, че условието на теоремата е и необходимо.