21. Метод на най-малките квадрати при косвени наблюдения

21.3. Алгоритъм на МНК за измервания без ограничения

21.1. Линеен случай

Сега предполагаме, че имаме няколко неизвестни величини: . Обикновено ние не измерваме пряко самите величини, които ни интересуват, а някакви техни функции. Означаваме тези функции с и предполагаме засега, че те са линейни:

(1)

В матричен вид системата (1) се записва така:

(2)

Тук и са -мерни вектори (стълбове), а матрица.

Ние пак смятаме, че всяко измерване съдържа грешка и че . Самите резултати от измерванията означаваме с :

(3)

Предполагаме, че измерванията са независими. Следователно, ковариационната матрица на (същата е и на ) е диагонална и има вида:

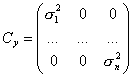
(4)

Обратната матрица на се нарича тегловна матрица на измерванията. В нашия случай (ур.(4)) тя се получава лесно:

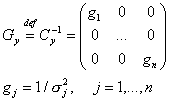(5)

Заместваме (3) в (2) и получаваме:

(6)

Това е система линейни уравнения спрямо . Ще търсим решение на тази система в духа на метода на максималното правдоподобие (тъй като тази система е преопределена при брой на неизвестните по-малък от този на измерванията, , което е обичайният случай. Ако , решението е единствено и няма какво повече да се прави). По предположение грешките (а от (3) това следва и за ) са разпределени нормално, т.е.:

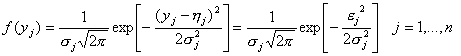(7)

Функцията на правдоподобие, респ. логаритмичната функция на правдоподобие ще бъдат:

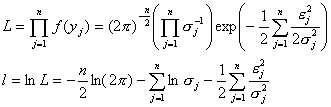(8)

Очевидно, ММП изисква да търсим максимума на , който съвпада с минимума на , където:

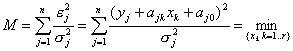(9)

(сумирането по се подразбира). Или, в матричен вид се записва така (този запис е валиден и когато измерванията не са независими, т.е. тегловната матрица няма простия диагонален вид (5)):

(10)

Минимумът на се постига, когато едновременно са изпълнени условията:

(11)

Това е равносилно на:

(12)

(последният резултат може да се провери чрез диференциране по компоненти). При това матрично уравнение (еквивалентно на система от линейни уравнения) може да се реши спрямо . За целта то се записва във вида:

(13)

Тогава решението му е:

(14)

По такъв начин най-добрите ММП-оценки за неизвестните величини се изразяват чрез измерванията , тяхната ковариационна матрица и известните коефициенти на функциите .

За съгласуване на означенията с по-нататъшните раздели въвеждаме съкращението:

(15)

което не зависи от . Тогава решението (14) се записва така:

(16)

Тук случаят на преки измервания се получава като частен случай.

Сега ще се спрем на въпроса за влиянието на грешките от измерванията върху оценките на неизвестните параметри . Тъй като (16) дава линейна връзка между неизвестните и измерванията , ние можем да използуваме закона за разпространение на грешките за определяне на дисперсиите (и ковариациите) на .

Нека е ковариационната матрица на . Тогава имаме:

(17)

За опростяване на израза вземаме предвид известното свойство на матриците и факта, че матриците са симетрични. Резултатът е:

(18)

И тъй, получихме проста форма за ковариационната матрица на най-добрите МНК-оценки за неизвестните . Квадратните корени от диагоналните елементи на (18) могат да се разглеждат като мерки за неопределеностите ("грешките") на неизвестните , макар и те да не се измерват непосредствено в експеримента. Недиагоналните елементи са, разбира се, мярка за корелациите на по двойки.

По-нататък, МНК-оценка за , т.е. (16) може да се използува за определяне на най-добрата (в смисъл на МНК) оценка за вектора на грешките :

(19)

Статистиката :

(20)

се подчинява на разпределение с степени на свобода.

Пример: Полиномната апроксимация като линейна задача на МНК

Нека е една независима променлива, а величините, които се измерват, са полиноми на :

(1)

Нека сме извършили измервания на за . Това са:

(2)

Предполагаме, че освен ние знаем и тяхната ковариационна матрица (най-често предполагаме, че са независими; тогава е достатъчно да познаваме ).

Системата линейни уравнения за ще има вида:

(3)

Очевидно, сега ще имаме: и:

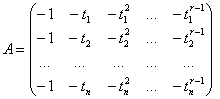(4)

Това е задачата за прекарване на най-добрия полином от степен през точки. Тази задача е най-популярното приложение на МНК.

21.2. Нелинеен случай

Досега предполагахме, че функционалните съотношения между измеряемите величини и неизвестните параметри са линейни. Сега ще се освободим от това ограничение и ще разгледаме общия случай.

И тъй, имаме:

(1)

Идеята е, както много често се прави, нелинейният случай да се сведе към линеен чрез развитие на нелинейните функции в ред на Тейлър (Taylor) и ограничаването на това разложение до линейни членове включително.

Нека е някакво начално приближение към стойностите на неизвестните параметри . Тогава:

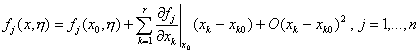(2)

Означаваме:

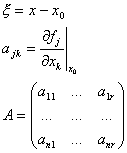(3)

Предполагаме, както и преди, че за фактическите резултати от измерванията е в сила:

(4)

Тогава:

(5)

Означаваме още:

(6)

Следователно:

(7)

Системата линейни уравнения (7) е напълно аналогична на линейния случай. Решението й е:

(8)

Това обаче сега е МНК-оценката за вектора на корекциите . Съответно, ковариационната матрица на ще бъде:

(9)

По същия начин (както за линейния случай) може да се получи оценка за уточнените грешки .

Тъй като началното приближение е фиксиран вектор, за вектора е в сила:

(10)

Сега вече можем да заменим с , да развием около и да повторим цялата процедура. Този итерационен процес може да се повтаря, докато поправките станат толкова малки, че уточненията за поредната стъпка да станат незначителни.

Тук не е показано, че такава процедура е сходяща и води към единствено решение. Нещо повече, това в общия случай не може и да се докаже (засега?) Сходимостта трябва да се проверява следователно във всеки конкретен случай.

Ясно е, че функциите не трябва да се отличават силно от линейни функции в околността на точките Или пък, алтернативно, ако са силно нелинейни, началното приближение трябва да е достатъчно близо до решението . Това е същността на изкуството за прилагане на МНК в нелинейния случай.

21.3. Алгоритъм на МНК за измервания без ограничения

Тук ще представим последователността на пресмятанията, необходими за получаването на решението на задачата за оценка на параметри по метода на най-малките квадрати за измервания без ограничения.

Дадени са:

· измервания, ;

· тяхната ковариационна матрица ;

· на брой измеряеми величини , които са известни функции на (евентуално) някакви независими променливи и на неизвестните параметри :

Дадено е също едно начално приближение за стойностите на неизвестните параметри: (-мерен вектор).

Следва схемата на итерационния процес за решаване на МНК-проблема:

0. Означаваме номера на итерацията с и полагаме . Пресмятаме тегловната матрица на измерванията: ;

1. Пресмятаме матрицата 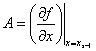и вектора ;

2. Пресмятаме - ковариационната матрица на неизвестните в това приближение;

3. - вектора на корекциите и оценките за грешките на измерванията;

4. - неизвестните параметри в това приближение;

5. .

6. Ако е постигната сходимост (вж. по-долу), приключваме пресмятанията. Текущото решението се съдържа в . В противен случай, увеличаваме номера на итерацията и се връщаме към точка 1.

Критериите за постигане на сходимост на итерационната процедура могат да са следните:

· : (в две последователни итерации стойностите на статистиката се различават незначително); това е белег, че минимумът на е практически достигнат;

· (нормата на вектора на корекциите за дадена итерация е незначителна; тук нормата е мярка за дължината на вектора, напр. Евклидовата норма е: 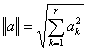); това означава, че корекциите вече са достатъчно малки.

Тези два критерия могат да се прилагат поотделно или в някаква комбинация помежду им. Освен това трябва да се предвидят и резервни изходи:

· изход при достигане на някакъв предварително определен максимален брой итерации, независимо от това дали е постигната сходимост;

· изход при разходимост (), тъй като, както отбелязахме, МНК-процедурата не е гарантирано сходяща; това се случва нерядко при лоши начални приближения.