Общи бележки

Методът на най-малките квадрати (МНК, least-squares) е създаден от Льожандър (Legendre) и Гаус (1805-1809) първоначално въз основа на интуитивни съображения. В първоначалния си вид това правило е изглеждало така:

Резултатите от многократните наблюдения на неизвестната величина се разглеждат като сума от истинската величина и някаква добавъчна грешка:

(1)

Правилото гласи, че стойността на неизвестната величина трябва да се определи от условието за минимум на сумата от квадратите на грешките:

(2)

В много случаи това правило може да бъде получено от метода на максималното правдоподобие (ММП, който е развит доста по-късно), което вече служи за сериозна обосновка на МНК. Но дори и в случаите, когато МНК не може да се получи чрез ММП, МНК-резултатите притежават редица благоприятни свойства (в сравнение с други методи за оценка). Поради това МНК е най-често използваният от всички статистически методи за обработка на данни и оценка на параметри.

Трябва да се разграничават следните случаи на употреба на МНК:

· при преки наблюдения - когато ние директно измерваме интересуващата ни величина;

· при косвени наблюдения - когато наблюдаваните величини са свързани с оценяваните параметри не пряко, а чрез някакви (известни или предполагаеми) функционални зависимости. С други думи, наблюдаваните величини са някакви функции - линейни (ЛМНК, linear least-squares) или нелинейни (НМНК, non-linear least squares) на търсените параметри;

· накрая, говорим за наблюдения с ограничения - когато между неизвестните параметри съществуват (или се предполагат) съотношения от определен функционален тип (пак се разграничават случаите на линейни и нелинейни ограничения);

· по-нататък, ограниченията могат да бъдат строги (ограничения от тип равенства) (напр. ограничението сумата от измеряемите ъгли на един триъгълник да е 180⁰) или пък ограничения от тип неравенства (напр. площите на спектралните линии да са неотрицателни).

Ние ще разглеждаме последователно различните варианти на МНК, започвайки от по-простите.

Метод на най-малките квадрати при преки наблюдения

Този случай е най-прост, но ние го разглеждаме специално, за да въведем някои означения и да очертаем основната схема на МНК.

Нека са извършени независими измервания на една (неизвестна) величина . Измерените стойности съдържат грешки от измерванията:

(1)

За грешките предполагаме, че са случайни величини, разпределени нормално около нулата:

(2)

Това предположение се оправдава в много случаи от централната гранична теорема.

Вероятността в резултат на измерването да получим стойност в интервала е:

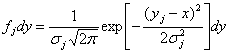(3)

Сега можем да конструираме функцията на правдоподобие и логаритмичната функция на правдоподобие. Те са, съответно:

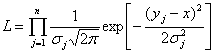(4)

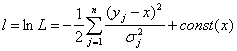(5)

Следователно, условието за максимум на съвпада с условието:

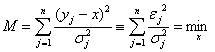(6)

което е точно условието на МНК. Виждаме, че в този най-прост случай МНК се получава непосредствено от ММП.

В интерес на единството на по-нататъшните означения ще въведем величините:

(7)

Те се наричат тегла на измерванията . При това получаваме:

(8)

Вижда се, че теглото на всеки от членовете в сумата (8) е обратно пропорционално на дисперсията на съответното измерване; следователно, по-малко точните измервания участвуват с по-малко тегло при определянето на резултата .

Самият резултат (т.е. оценката за стойността на неизвестната величина ), разбира се, може да се получи в този случай непосредствено чрез пресмятане на минимума на функционала :

(9)

Оттук:

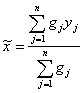(10)

това е претегленото средно аритметично на отделните измервания.

Ако всички дисперсии биха били равни (което би съответствало точно на условията за случаен избор от една и съща популация), тогава би съвпаднало точно със средното аритметично на извадката. Изразът (10) е по-общ, доколкото той отчита евентуалната нееднаква точност на измерванията.

Оценката на търсената величина , т.е. , е случайна величина, тъй като тя се получава чрез извадката. На нас ни е необходима оценка и за нейните статистически характеристики, на първо място за нейната дисперсия, която зависи от свойствата на първичните наблюдения , съдържащи случайните величини . Използвайки известните ни свойства за дисперсията на сума от случайни величини, за дисперсията на получаваме:

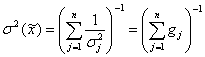(11)

(при равни дисперсии на измерванията получаваме известния ни резултат ).

Сега, тъй като грешките са случайни величини, техните средни стойности могат да бъдат оценени обратно чрез извадката в съответствие с вече полученото решение :

(12)

Оценките са също случайни величини и имат разпределение (същото като това на ). Следователно:

(13)

Но тогава ние знаем, че в точката на решението:

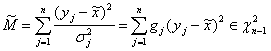(14)

има разпределение с степени на свобода (една степен се отнема от замяната ). Това свойство на величината може да се използува за проверка на първоначалната ни хипотеза, а именно, че (припомняме):

· са наблюдения на неизвестната величина ;

И така, статистиката (14) може да се използува за проверка на горната хипотеза. Как ставаше това? Ако за избраното ниво на значимост , , то ние се намираме в критичната област и трябва да отхвърлим хипотезата. Това означава или че (някои от) не са наблюдения на неизвестната величина , или че грешките . Първата възможност може да се дължи на някакво грубо въздействие върху апаратурата (смущение, "изхвърчали" точки и др.), когато резултатите от измерването не може да се считат за наблюдения само на неизвестната величина . Дори само едно води до много голямо , и по-нататъшната проверка става безсмислена. В такъв случай се постъпва така: взема се измерването с най-голямо отклонение () и му се приписва тегло нула, , т.е. това измерване се изключва от процеса на оценка. След това построяваме нова МНК-оценка за , . Ако за нея е значително по-малко, то трябва да изхвърлим измерването и да продължим с останалите наблюдения.

Понякога обаче е възможно първият пункт от изказаната по-горе хипотеза да е в сила, но грешките от измерванията да не са разпределени нормално; в частност, наблюденията могат да имат отместване спрямо нулата (напр. "пълзене" на апаратурата с времето и пр.). Това вече говори за систематични грешки в измерванията. В такъв случай оправдано от статистическа гледна точка е (ако не могат да се "набедят" само 1-2 измервания като неточни) да не се правят опити за МНК-оценки и позитивни заключения за резултатите от измерванията, докато не бъдат извършени по-нататъшни експерименти.